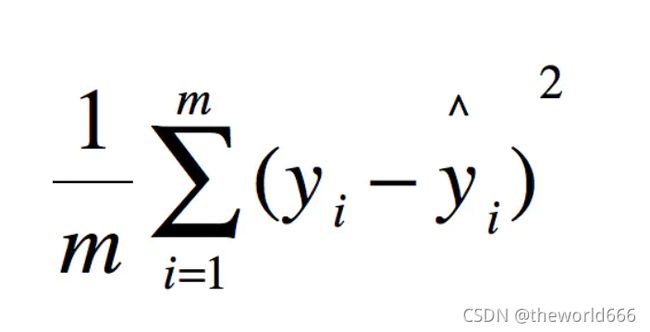机器学习算法学习01：利用Numpy编写KNN算法解决手写体数字识别问题

机器学习算法学习01：利用Numpy编写KNN算法解决手写体数字识别问题

前言

在深度学习未彻底被大众接受前，人们对人工智能的研究是企图研究出一系列巧妙的算法解决相关计算机视觉问题，这里面涌现了无数令人叹为观止的算法（随机森林，遗传算法，SVM，马尔科夫链，KNN等）即使在深度学习逐渐占据解决计算机视觉人工智能问题的算法的今天，不可否认，依旧有许多深度学习算法吸收了这些传统算法的思想，从而来进行改进，所以学习这些传统算法也是非常有必要的。本次我们介绍的是如何利用numpy库来构造KNN算法解决手写体数字识别问题。

本篇博客的代码也已上传到github仓库，不麻烦的话可以点颗星：

liujiawen-jpg/KNN-Alogorith: The KNN algorithm is implemented by numpy (github.com)

1.算法介绍

KNN算法全称（K-NearestNeighbor）直译为K个最近的邻居，是一种聚类算法。该算法认为我们在判断一个物体的类别可以根据与他非常相似的K个物体的类别（这K个物体的类别是已知的）来决定。

举个例子，假设我们需要鉴别某个水果的类别，我们通过比对发现他和我们拥有的水果中7个物品非常相似，我们发现这七个物品其中6个是西瓜，一个是菠萝，所以我们自然的认为这个物品是西瓜。这就是一个7NN算法。

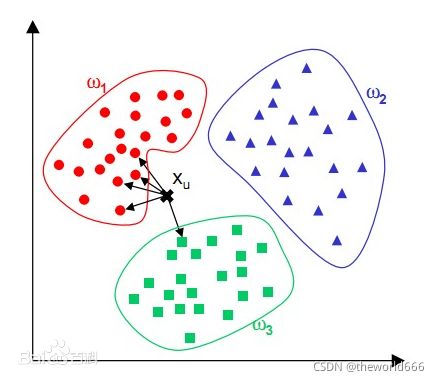
直观一点，我们可以观察上图。该图之中存在三个类别ω1，ω2 ω3。我们使用5NN寻找五个与X相邻最近的点发现其中四个属于ω1那么我们就可以推断出X属于ω1类别。

看了上面两个例子，相信你应该对KNN算法有了基础的认识了吧，那么我们这里可以先总结出他的流程：

输入：数据x 已知类别的样本z 输出：x的类别y

开始

1. 计算数据x与z中每个样本的距离d

2. 利用距离d获取与x距离前K小的索引index

3. 利用index从样本z中选取出k个样本

4. 统计这k个样本的类别，类别数统计最多的作为x的类别

   结束

2.数据集介绍

这里我们使用的是sklearn库提供的手写体数据集，该数据集包括了1797张手写的0-10的图片

import sklearn.datasets as datasets  
import matplotlib.pyplot as plt
import random
x, y = datasets.load_digits(return_X_y=True) #获取训练集和样本
# 这里我们可以可视化图片来进行查看
x1 = random.choice(x) # 随机取出x中的数据
x1 = np.array(x1)
x1 = np.reshape(x1, (8,8)) # 取出来的向量被压缩成了64的序列，而要显示成图片我们需要将他改成二维的形状
plt.imshow(x1)
plt.show()

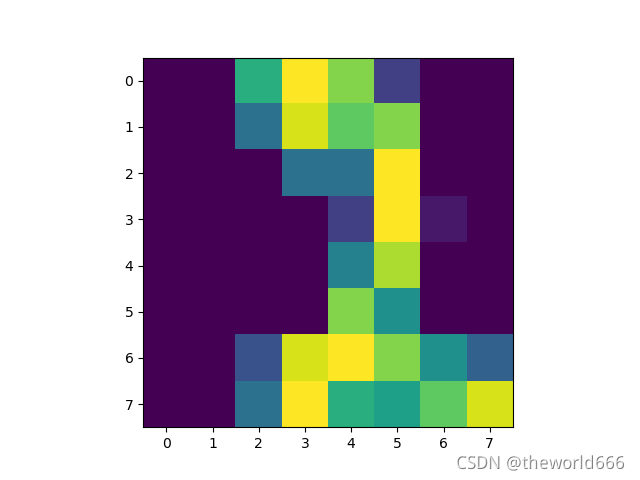
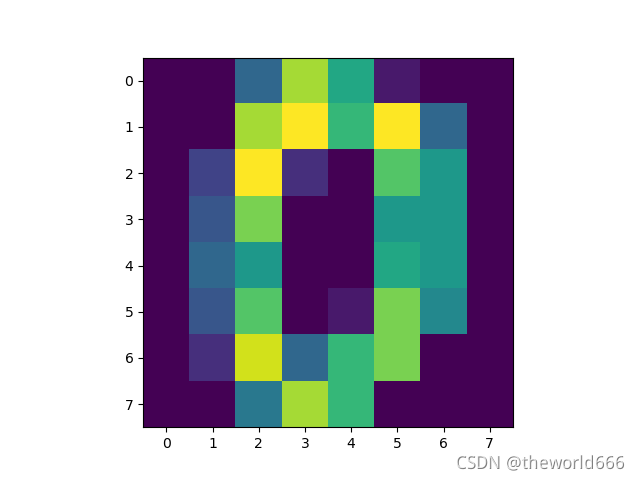
通过以上的代码我们可以查看图片的内容，我们看出来这些其实就是一系列0-10的图片（如下两张就是0和2）（由于设置的是随机取出，所以可以多运行几次，每次运行的结果都不一样）

3.先决条件：安装numpy,sklearn库

python由于他的方便简单，前人开发了无数的易于使用的库，但是这些并不会随着你的安装而自动安装（sklearn库好像会自动安装），所以我们需要自己输入命令来安装，不过也是非常简单的这里如果遇到不知道使用什么命令可以查看这个网站：

Search results · PyPI

利用这个网站查询结果如下，我们复制命令 pip install numpy即可

然后我们如果是在windows系统上直接，同时按下win键和R键，在弹出的窗口中输入cmd并执行，最后在弹出的命令行界面中输入查询到的命令：

pip install numpy

等待下载完成即可，如果遇到下载速度非常慢的话可以使用这个博客的方法（解决 ERROR: Could not find a version that satisfies the requirement xxx 的问题_JMU-HZH的博客-CSDN博客）

安装sklearn库也同理。

4.算法代码编写

在此次手动实现KNN算法中，我一共写了两个py文件，KNN.py和run.py。其中KNN.py实现了kNN算法，而run.py则为程序启动脚本，让我们来一一介绍吧️‍♂️️‍♂️️‍♂️：

KNN.py

import numpy as np
class KNN():
    def __init__(self, x_test, x_train, k):
        
        self.neighbor_distance = np.zeros((len(x_test), len(x_train)))
        #neighbor_distance数组记录测试数据与已知样本数据的距离
        self.pred = np.zeros(len(x_test,))
        # pred数组记录所有样本的预测值
        self.neighbors = k
        # 记录需要找出多少个近邻

    def knn(self, x_test, x_train, y_train):
        for i in range(len(x_test)):
            for j in range(len(x_train)):
                self.neighbor_distance[i][j] = self.compute_distance(
                    x_test[i], x_train[j]) #计算所有的测试数据和样本数据的距离
            self.pred[i] = self.compute_pred(
                self.neighbor_distance[i], y_train) #获得所有样本数据的预测值
        return self.pred

    def compute_distance(self, x, y):
        # 这里使用mae来进行计算距离
        distance = np.sum(np.abs(x - y))
        # 也可以使用mse来进行计算两者的距离
        # distance = np.sum(np.square(x - y))
        return distance

    def compute_pred(self, distance, y_train):
        k_pred_index = distance.argsort()[:self.neighbors] #利用numpy的argsort方法获取前K小样本的索引
        k_pred = [y_train[index] for index in k_pred_index]#获取与测试数据最接近K个物体的类别
        pred = np.argmax(np.bincount(k_pred)) #计算哪个类别出现的最多作为测试数据的类别
        return pred

run.py:

import numpy as np
import sklearn.datasets as datasets  # 数据集模块
from sklearn.model_selection import train_test_split  # 划分训练集和验证集
import matplotlib.pyplot as plt
import random
from KNN import KNN
# 读取数据集
x, y = datasets.load_digits(return_X_y=True)

# 使用sklearn中的方法划分我们的测试数据和训练数据
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2)

# KNN最近邻进行分类，这里的K数字可以任意改变
k = 7
knn = KNN(x_test, x_train, k) #初始化我们的knn类别
pred = knn.knn(x_test, x_train, y_train) #获取预测值

# 利用numpy提供的函数计算分类准确率
accuracy = np.mean(pred == y_test)
print(accuracy)

5.实验结果分析

在本次实验中存在三个可供我们调整的变量，分别是测试数据与训练数据的比值，计算距离的方法，选取的近邻个数K。接下来我们使用控制变量法来修改他们观察正确率的变化。

先给定我们的baseline，当测试数据与训练数据数量比为 1 ：4，计算距离采用mae平均绝对误差时准确率为0.986

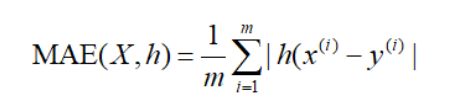
5.1 保持其他变量不变，修改计算距离方式

1.计算距离采用mse(均方绝对误差)：

多次实验正确率为0.994到0.97，取二者平均值计算约为0.986

2 计算距离采用RMSE(均方根误差)方式:

多次实验正确率稳定在0.978左右

5.2 保持其他变量不变，修改k的个数

k = 3, accuracy = 0.983

k=4, accuracy = 0.986

k = 5 accuracy = 0.986

k=6, accuracy = 0.972

k=7,accuracy = 0.985

k=8,accuracy = 0.978

k=9,accuracy=0.980

k=10, accuracy=0.971

5.3 保持其他变量不变，修改测试数据与训练样本的比值

比值为 3:7 , accuracy=0.976

比值为4:6，accuracy = 0.976

比值为1:1, accuracy = 0.971

比值为6:4，accuracy= 0.967

比值为7:3，accuracy=0.965

比值为8:2，accuracy=0.949

比值为9:1，accuracy=0.869

通过以上三个控制变量实验，我们可以发现

• 修改计算数据与数据之间距离方式对提升正确率并无太大作用，其中使用mae和mse效果最好，RMSE效果较差
• 可以看出来当K的值越发上升时正确率开始逐渐下降，可能是由于当决定数据类别的“近邻”太多时噪声过多影响了精度
• 而调整测试数据与训练样本的比值则会影响正确率，可以看到当测试数据越来越多训练样本越来越少模型正确率越来越低吗，我们可以看出使用KNN我们的训练样本必须尽可能地多，以保证我们的准确率。

补充实验

另一个是博主学习的教材提供的约会网站数据集（Manning | Machine Learning in Action），该网站数据统计每个用户的三种数据：

• 每年获得的飞行常客里程数
• 玩视频游戏(video games)所耗时间百分比
• 每周消耗的冰淇淋公升数

并将所有人分为三类：

• 不喜欢的人
• 魅力一般的人
• 极具魅力的人

我们的问题就变成了根据上面三个统计数据，将用户进行分类。

数据被放在一个TXT的文件夹中，其中每行共四个数据，前三个为前面提到的三个统计数据，后一个为用户的分类结果。我们按照这样的格式制作读取文件函数：

def file2Matrix(filename):
    fr = open(filename)
    arrayOLines = fr.readlines() #按照行数来读取文件
    numberOfLines = len(arrayOLines) #统计数据个数
    returnMat = zeros((numberOfLines, 3)) # 输入向量为三维的
    classLabelVector = []
    index = 0
    for line in arrayOLines:
        line = line.strip()
        listFromLine = line.split('\t')
        returnMat[index,:] = listFromLine[0:3]
        classLabelVector.append(int(listFromLine[-1])) #标签向量
        index += 1
    return returnMat, classLabelVector #返回被格式化后的统计数据和标签

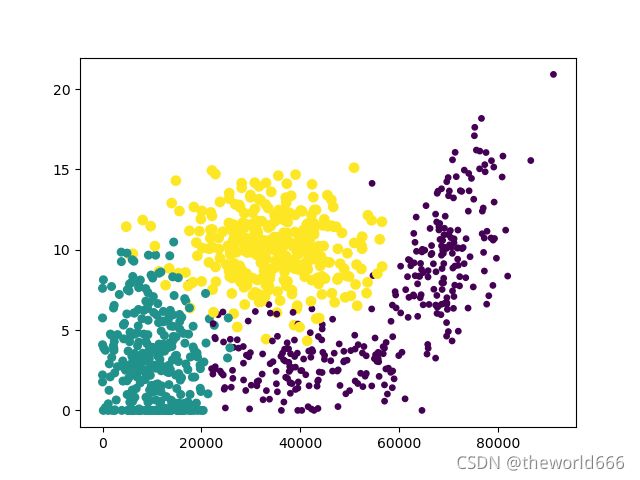
获得这些统计数据之后，我们可以使用绘图库进行绘制图片来可视化数据：

import numpy as np
import matplotlib.pyplot as plt
    Data, label = file2Matrix('datingTestSet2.txt')
    fig = plt.figure()
    # plt.scatter()
    ax = fig.add_subplot(111)
    ax.scatter(Data[:,0], Data[:,1], 15.0*np.array(label), 15.0*np.array(label))
    #后两个参数一个表示size,一个表示color，我们可以利用分类大小1,2,3从而区分夜色和大小，可以看到三个类别的区分非常的清晰
    plt.show()

但有时候我们需要注意，就是这些输入特征的数量级到底是不是一致的（如果是手写体识别我们并不需要注意这个问题），比如说一个人的飞行里程数可能有达到万里程级别，但是一个人吃冰淇淋可能一周只能吃几升，这会导致比起其他条件，飞行里程数实际上更影响我们的分类结果，权重更大。所以我们还需要对所有输入特征进行归一化，将所有输入特征的数值降低到[0,1]之间，消除数量级的差别，从而使所有输入特征对分类结果的影响保持一致。

# 这里我们使用的归一化方法是将所有数据减去数据中的最小值，除以最大值与最小值之差
def autoNorm(dataSet):
    minValues = dataSet.min(0)
    maxValues = dataSet.max(0)
    ranges = maxValues - minValues
    normDataSet = zeros(shape(dataSet))
    m = dataSet.shape[0]
    normDataSet = dataSet-tile(minValues, [m,1])
    normDataSet = normDataSet/tile(ranges, (m,1))
    return normDataSet, ranges, minValues

normData, _ ,_ = autoNorm(Data) #对数据进行归一化，我们并不关心后面返回的数据，使用占位符来接收
print(np.max(normData),np.min(normData)) #查看数据的最大值，最小值，验证数据是否被缩小到0和1之间
#结果如果输出1.0 0.0，说明我们的归一化结果是正确的 

我们的数据在归一化完之后，接下来就可以使用KNN算法来对它进行分类了：

import operator
import os
from numpy import *
#这个kNN算法的复用性我个人认为极高，几乎所有的kNN问题转换下格式都可以使用他来解决
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]
    diffMat = tile(inX, (dataSetSize,1)) - dataSet # 这个会将输入数据重复到
    sqDiffMat = diffMat**2 
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5 #这里我们使用欧式距离将特征之差的平方和开根号作为我们的距离
    sortedDistIndicies = distances.argsort()
    classCount={
     }
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #将标签结果进行排序
    return sortedClassCount[0][0] #返回统计标签


#我们在将数据输入算法之前还需要转换一下格式
def datingClassTest():
    hoRatio = 0.10 #测试集占原有数据集的比例
    datingDataMat,datingLabels = file2Matrix('datingTestSet2.txt') #读取数据
    normData, ranges, minVals = autoNorm(datingDataMat) # 归一化数据
    m = normData.shape[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classfileResult = classify0(normData[i,:], normData[numTestVecs:m,:],\
                                    datingLabels[numTestVecs:m],10)
        if(classfileResult!=datingLabels[i]):
            errorCount +=1.0 # 统计错误个数
    print("the total accuray is: ", (1-(errorCount/float(numTestVecs)))*100) #统计百分比正确率
datingClassTest()

#输出结果为百分比正确率，94% 

结语

在本次实验中，我完成了独立编写kNN算法的任务，并通过控制变量法完成了对于kNN中各个变量影响性能的研究。同时我也认识到传统机器学习算法的设计巧妙，即使在深度学习一统江湖的今天，它对我们这些人工智能的后来者依旧具有非常好的启示意义，值得我们去认真学习。