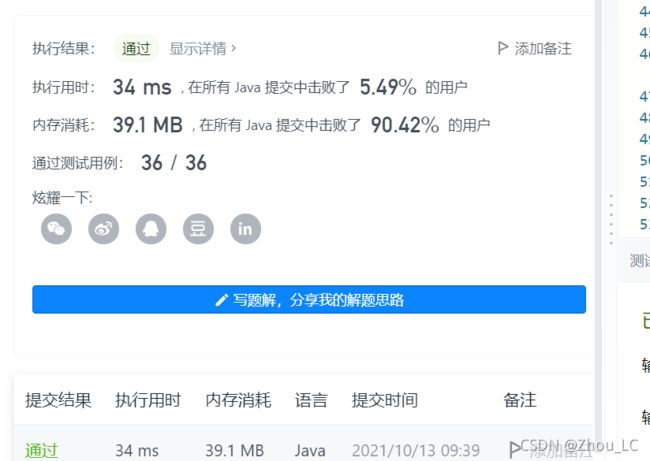
【算法】贪心算法:LeetCode 406 根据身⾼重建队列 、LeetCode 452 用最少数量的箭引爆气球
LeetCode 406:根据身高重建队列
(中等)
题目
描述
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
思路
对于这样有两个维度需要参考的情况,即最终结果既需要参考身高h,也需要参考个数k,因此,正确的思路是需要先确定下其中一个参考维度,再去解决另一个参考维度,题目中已说明每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人,因此我们可以先创建一个用于存储最终结果的二维数组变量 queue,之后,按身高,也就是 people[0][i],对原二维数组 people 数组进行从大到小的排序,这样,我们按顺序从降序的 sortedPeople 中取出每一个元素(一维数组),插入到 queue 的 sortedPeople ki 位置,这样每次 queue 中的元素的身高值,都是大于当前 sortedPeople 取出的元素的,而 sortedPeople ki 要规定前面有多少个大于当前元素身高的元素,因此,直接将新取出的元素插入到 queue 的 ki 位置即可。因此局部最优是:优先按身⾼⾼的people的k来插⼊。插⼊操作过后的people满⾜队列属性,全局最优是:最后都做完插⼊操作,整个队列满⾜题⽬队列属性。(但是当时思路里面有个致命的漏洞,导致提交错误 —— 无法处理身高相等的情况)
public class TX11根据身高重建队列 {
public int[][] reconstructQueue(int[][] people) {
if (people == null || people.length == 0) {
return null;
}
int[][] queue = new int[people.length][people[0].length];
//先按people[0][i]即身高进行从大到小的排序
int[][] sortedPeople = sort(people);
for (int i = 0; i < sortedPeople.length; i++) {
insert(queue, sortedPeople[i], sortedPeople[i][1]);
}
return queue;
}
/**
* 向二维数组中插入一维数组
* @param deepArray
* @param array
*/
public void insert(int[][] deepArray, int[] array, int index) {
for (int i = deepArray.length - 1; i > index; i--) {
deepArray[i] = deepArray[i - 1];
}
deepArray[index] = array;
}
/**
* 冒泡排序算法:对二维数组按array[0][i]进行排序
* @param array
* @return
*/
public int[][] sort(int[][] array) {
int i, j;
int len = array.length;
//拷贝一份
int[][] copy = new int[len][array[0].length];
for (i = 0; i < len; i++) {
copy[i] = Arrays.copyOf(array[i], array[0].length);
}
boolean flag = true;
for (i = 0; i < len - 1 && flag; i++) {
flag = false;
for (j = len - 2; j >= i; j--) {
if (copy[j][0] < copy[j + 1][0]) {
swap(copy, j, j + 1);
flag = true;
}
}
}
return copy;
}
/**
* 交换二维数组中的两个一维数组的位置
* @param array
* @param i
* @param j
*/
public void swap(int[][] array, int i, int j) {
int[] tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
TX11根据身高重建队列 s = new TX11根据身高重建队列();
System.out.println("s.reconstructQueue(new int[][]{
{7,0},{4,4},{7,1},{5,0},{6,1},{5,2}}) = " + Arrays.deepToString(s.reconstructQueue(new int[][]{
{
7, 0}, {
4, 4}, {
7, 1}, {
5, 0}, {
6, 1}, {
5, 2}})));
}
}

因未考虑身高相等这种情况而出现了错误:
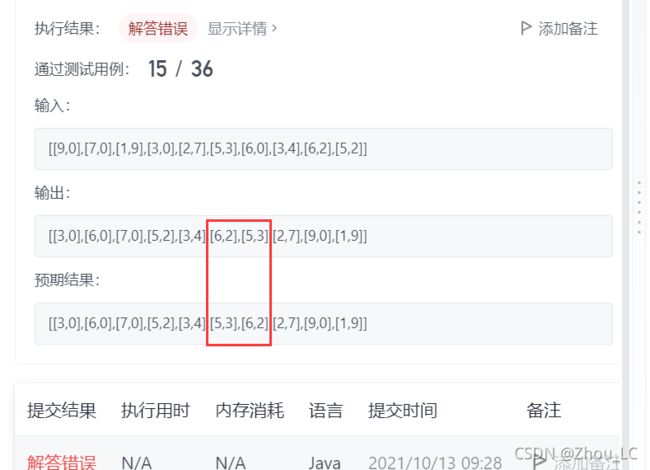
之后在 IDEA 中调试,也发现确实是这个问题引起的上述这种例子的报错:
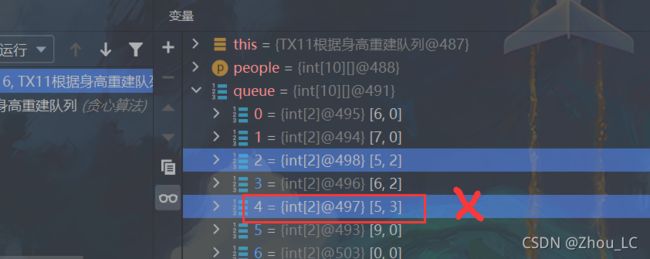
之后看官方的题解,发现了这种情况的思路:

因此,我们只需要在排序时,对于身高相等的情况,再对两者中的 k 进行比较,让 k 值较大的在后面即可,因此,我这里只需要改一下冒泡排序的算法即可。
在交换判断那,加上 || (copy[j][0] == copy[j + 1][0] && copy[j][1] > copy[j + 1][1])
if (copy[j][0] < copy[j + 1][0] || (copy[j][0] == copy[j + 1][0] && copy[j][1] > copy[j + 1][1])) {
swap(copy, j, j + 1);
flag = true;
}
实现
最终的代码:
public class TX11根据身高重建队列 {
public int[][] reconstructQueue(int[][] people) {
if (people == null || people.length == 0) {
return null;
}
int[][] queue = new int[people.length][people[0].length];
//先按people[0][i]即身高进行从大到小的排序
int[][] sortedPeople = sort(people);
for (int i = 0; i < sortedPeople.length; i++) {
insert(queue, sortedPeople[i], sortedPeople[i][1]);
}
return queue;
}
/**
* 向二维数组中插入一维数组
* @param deepArray
* @param array
*/
public void insert(int[][] deepArray, int[] array, int index) {
for (int i = deepArray.length - 1; i > index; i--) {
deepArray[i] = deepArray[i - 1];
}
deepArray[index] = array;
}
/**
* 冒泡排序算法:对二维数组按array[0][i]进行排序
* @param array
* @return
*/
public int[][] sort(int[][] array) {
int i, j;
int len = array.length;
//拷贝一份
int[][] copy = new int[len][array[0].length];
for (i = 0; i < len; i++) {
copy[i] = Arrays.copyOf(array[i], array[0].length);
}
boolean flag = true;
for (i = 0; i < len - 1 && flag; i++) {
flag = false;
for (j = len - 2; j >= i; j--) {
if (copy[j][0] < copy[j + 1][0] || (copy[j][0] == copy[j + 1][0] && copy[j][1] > copy[j + 1][1])) {
swap(copy, j, j + 1);
flag = true;
}
}
}
return copy;
}
/**
* 交换二维数组中的两个一维数组的位置
* @param array
* @param i
* @param j
*/
public void swap(int[][] array, int i, int j) {
int[] tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
TX11根据身高重建队列 s = new TX11根据身高重建队列();
System.out.println("s.reconstructQueue(new int[][]{
{7,0},{4,4},{7,1},{5,0},{6,1},{5,2}}) = " + Arrays.deepToString(s.reconstructQueue(new int[][]{
{
7, 0}, {
4, 4}, {
7, 1}, {
5, 0}, {
6, 1}, {
5, 2}})));
}
}
LeetCode 452:用最少数量的箭引爆气球
(中等)
题目
描述
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例1
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球
示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]]
输出:4
示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]]
输出:2
示例 4:
输入:points = [[1,2]]
输出:1
示例 5:
输入:points = [[2,3],[2,3]]
输出:1
思路
此题与上一题类似,都是二维数组的问题,都是有两个参数作为判断标准,统计最终结果,因此,也是先确定一个参数,对于此题来说,二维数组中每个一维数组存放横坐标的开始与结束位置,也就是可以先将横坐标开始位置按从小到大进行排序,这样才方便找出连续交叠摆放的气球,一箭引爆多个,从而统计最小的箭数。遍历横坐标初始值已经有序的数组序列,如果下一个气球的初始下标小于等于当前气球的结束下标,那么两气球是交叠放置的,并且,由于下一个的下一个气球甚至后续气球也可能与之交叠,因此,我们需要更新下一个气球的结束下标,让它每次都为两个交叠气球中,横坐标结束值中较小的那个,这样,才能在接下来的判断中,仍然保证前面的交叠也是成立的;如果不交叠,那么自然就是将箭数加1,需要消耗一支弓箭。

(但是在提交时,由于我的排序算法用的是冒泡排序,因此出现了超时的情况,而此题的逻辑代码是 O(n),是完全没有超时可能的,因为这里的效率瓶颈主要是排序算法引起的,因此我便将排序算法改为了快速排序,便可以提交成功)

实现
public class TX12用最少数量的箭引爆气球 {
public int findMinArrowShots(int[][] points) {
int[][] copy = new int[points.length][points[0].length];
for (int i = 0; i < points.length; i++) {
copy[i] = Arrays.copyOf(points[i], points[0].length);
}
sort(copy);
int arrowNum = 1;
for (int i = 0; i < copy.length - 1; i++) {
if (copy[i + 1][0] <= copy[i][1]) {
//i 与 i+1 交叠
copy[i + 1][1] = Math.min(copy[i][1], copy[i + 1][1]);
} else {
//不交叠
arrowNum++;
}
}
return arrowNum;
}
public void sort(int[][] a) {
int n = a.length - 1;
QSort(a, 0, n);
}
private void QSort(int[][] a, int low, int high) {
int pivot; // 枢轴的下标,将某个数放在此位置,使得它左边的值都比它小,右边的都比它大
if (low < high) {
pivot = Partition(a, low, high); // 将a[low..high]一分为二,算出枢轴下标pivot
QSort(a, low, pivot - 1); // 对低子表递归排序
QSort(a, pivot + 1, high); // 对高子表递归排序
}
}
// 交换顺序表a中子表的记录,使枢轴记录到为,并返回其位置
private int Partition(int[][] a, int low, int high) {
int pivotkey = a[low][0]; // 用子表的第一个记录作枢轴记录
while (low < high) {
// 从表的两端交替向中间扫描
while (low < high && a[high][0] >= pivotkey) {
high--;
}
swap(a, low, high); // 将比枢轴值小的记录交换到低端
while (low < high && a[low][0] <= pivotkey) {
low++;
}
swap(a, low, high); // 将比枢轴值大的记录交换到高端
}
return low; // 最终low == high,所有返回枢轴所在位置
}
/**
* 交换二维数组中的两个一维数组的位置
* @param array
* @param i
* @param j
*/
public void swap(int[][] array, int i, int j) {
int[] tmp = array[i];
array[i] = array[j];
array[j] = tmp;
}
public static void main(String[] args) {
TX12用最少数量的箭引爆气球 s = new TX12用最少数量的箭引爆气球();
System.out.println("s.findMinArrowShots(new int[][]{
{10,16},{2,8},{1,6},{7,12}}) = " + s.findMinArrowShots(new int[][]{
{
10, 16}, {
2, 8}, {
1, 6}, {
7, 12}}));
System.out.println("s.findMinArrowShots(new int[][]{
{1, 2}, {3, 4}, {5, 6}, {7, 8}}) = " + s.findMinArrowShots(new int[][]{
{
1, 2}, {
3, 4}, {
5, 6}, {
7, 8}}));
System.out.println("s.findMinArrowShots(new int[][]{
{9, 12}, {1, 10}, {4, 11}, {8, 12}, {3, 9}, {6, 9}, {6, 7}}) = " + s.findMinArrowShots(new int[][]{
{
9, 12}, {
1, 10}, {
4, 11}, {
8, 12}, {
3, 9}, {
6, 9}, {
6, 7}}));
}
}