人工智能学习笔记 python实现梯度下降法对多元函数求解
学习来自
梯度下降基本步骤如下图所示
我们以一个二元函数为例计算
设一个二元函数为
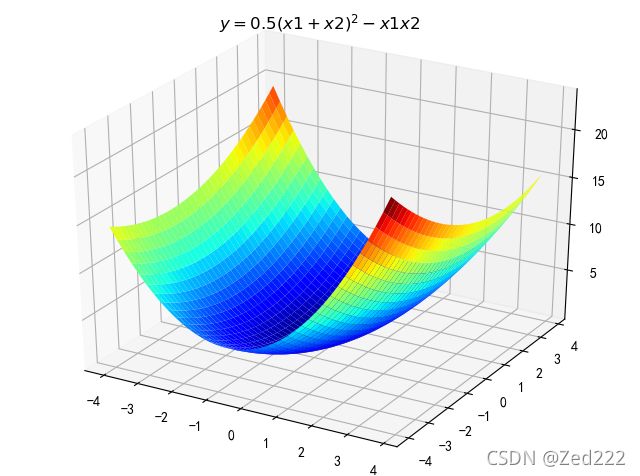
y=0.5*(x1+x2)^2-x1*x2一、则生成原函数图像代码如下
#一、构建一个函数为 y=0.5*(x1+x2)^2-x1*x2的图像
#原函数如下
# 二维原始图像
def f2(x, y):
return 0.15 * (x + 0.5) ** 2 + 0.25 * (y - 0.25) ** 2 + 0.35 * (1.5 * x - 0.2 * y + 0.35 ) ** 2
X1=np.arange(-4,4,0.2)
X2=np.arange(-4,4,0.2)
#Y = np.array(list(map(lambda t: f1(t),X)))
#Y = np.array(list(map(f2,zip(X1,X2))))
#print(Y)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv,将X1、X2变成n*m的矩阵,方便后面绘图
Y = np.array(list(map(f2,X1.flatten(),X2.flatten())))#这里压缩成一维
Y.shape = X1.shape # 1600的Y图还原成原来的(40,40)生成的图片如下
二、梯度下降步骤
1.随机初始化参数值θ
2.计算梯度 这个点分别求关于x1、x2的偏导数,x1 =x1 - α*(dY/dx1),x2 =x2 - α*(dY/dx2)
3.修改参数值 alpha表示学习步长,也就是每次按照梯度减少的方向变化多少
4.按照3)迭代更新θ值,直至收敛或者θ 值的改变小于设定的阈值
# #初始化参数θ 阈值 和学习步长
x1 = 4
x2 = 4
alpha = 0.5
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量delta和迭代次数 阈值=limit
delta = 100
iter_num = 0
limit = 1e-9 # #计算梯度
def hx1(x, y):
return 0.15 * 2 * (x + 0.5) + 0.25 * 2 * (1.5 * x - 0.2 * y + 0.35 ) * 1.5
def hx2(x, y):
return 0.25 * 2 * (y - 0.25) - 0.25 * 2 * (1.5 * x - 0.2 * y + 0.35 ) * 0.2开始递归
while delta > limit :
tmp_x1 = x1 - alpha * hx1(x1,x2)
tmp_x2 = x2 - alpha * hx2(x1,x2)
tmp_y = f2(tmp_x1,tmp_x2)
delta = np.abs(tmp_y - f2(x1,x2))
x1 = tmp_x1
x2 = tmp_x2
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(tmp_y)
iter_num += 1
print(u"当前结果为:(%.5f, %.5f, %.5f)" % (x1, x2, tmp_y))
print(u"迭代次数:%d" % iter_num)
迭代过程输出记录
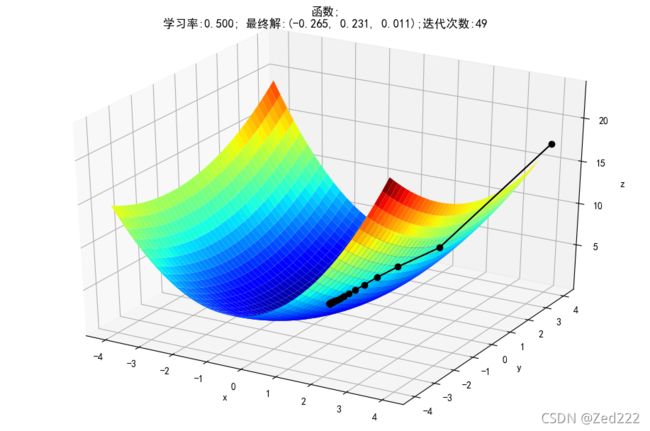
三、画图步骤
fig = plt.figure(facecolor='w',figsize=(10,8))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title(u'函数;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f2(x1,x2), iter_num))
plt.show()得出最终图像为
梯度下降最终代码
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
import random
from mpl_toolkits.mplot3d import Axes3D
import warnings
# 解决中文显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
#一、构建一个函数为 y=0.5*(x1+x2)^2-x1*x2的图像
#原函数如下
# 二维原始图像
def f2(x, y):
return 0.15 * (x + 0.5) ** 2 + 0.25 * (y - 0.25) ** 2 + 0.35 * (1.5 * x - 0.2 * y + 0.35 ) ** 2
X1=np.arange(-4,4,0.2)
X2=np.arange(-4,4,0.2)
#Y = np.array(list(map(lambda t: f1(t),X)))
#Y = np.array(list(map(f2,zip(X1,X2))))
#print(Y)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv,将X1、X2变成n*m的矩阵,方便后面绘图
Y = np.array(list(map(f2,X1,X2)))#这里压缩成一维
Y.shape = X1.shape # 1600的Y图还原成原来的(40,40)
# #二、梯度下降步骤
# # 1.随机初始化参数值θ
# # 2.计算梯度 这个点分别求关于x1、x2的偏导数,x1 =x1 - α*(dY/dx1),x2 =x2 - α*(dY/dx2)
# # 3.修改参数值 α表示学习步长,也就是每次按照梯度减少的方向变化多少
# # 4.按照3)迭代更新θ值,直至收敛或者θ 值的改变小于设定的阈值
# #计算梯度
def hx1(x, y):
return 0.15 * 2 * (x + 0.5) + 0.25 * 2 * (1.5 * x - 0.2 * y + 0.35 ) * 1.5
def hx2(x, y):
return 0.25 * 2 * (y - 0.25) - 0.25 * 2 * (1.5 * x - 0.2 * y + 0.35 ) * 0.2
# #初始化参数θ 阈值 和学习步长
x1 = 4
x2 = 4
alpha = 0.5
#保存梯度下降经过的点
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定义y的变化量和迭代次数
delta = f2(x1,x2)
iter_num = 0
limit = 1e-9
while delta > limit :
tmp_x1 = x1 - alpha * hx1(x1,x2)
tmp_x2 = x2 - alpha * hx2(x1,x2)
tmp_y = f2(tmp_x1,tmp_x2)
delta = np.abs(tmp_y - f2(x1,x2))
x1 = tmp_x1
x2 = tmp_x2
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(tmp_y)
iter_num += 1
print(u"当前结果为:(%.5f, %.5f, %.5f)" % (x1, x2, tmp_y))
print(u"迭代次数:%d" % iter_num)
#print(GD_X1)
# 作图
fig = plt.figure(facecolor='w',figsize=(10,8))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title(u'函数;\n学习率:%.3f; 最终解:(%.3f, %.3f, %.3f);迭代次数:%d' % (alpha, x1, x2, f2(x1,x2), iter_num))
plt.show()