视觉SLAM十四讲CH3代码解析及课后习题详解

eigenMatrix.cpp

#include 

using namespace std;

#include 
// Eigen 核心部分
#include 
// 稠密矩阵的代数运算（逆，特征值等）
#include 

using namespace std;
using namespace Eigen;

#define MATRIX_SIZE 50 宏定义 矩阵大小50

/****************************
* 本程序演示了 Eigen 基本类型的使用
****************************/

int main(int argc, char **argv) {
  // Eigen 中所有向量和矩阵都是Eigen::Matrix，它是一个模板类。它的前三个参数为：数据类型，行，列
  // 声明一个2*3的float矩阵
  Matrix matrix_23;

  // 同时，Eigen 通过 typedef 提供了许多内置类型，不过底层仍是Eigen::Matrix
  // 例如 Vector3d 实质上是 Eigen::Matrix，即三维向量
  Vector3d v_3d;
  // 这是一样的
  Matrix vd_3d;//声明一个3*1的float矩阵

  // Matrix3d 实质上是 Eigen::Matrix
  Matrix3d matrix_33 = Matrix3d::Zero(); //初始化为零
  // 如果不确定矩阵大小，可以使用动态大小的矩阵
  Matrix matrix_dynamic;
  // 更简单的
  MatrixXd matrix_x;
  // 这种类型还有很多，我们不一一列举

  // 下面是对Eigen阵的操作
  // 输入数据（初始化）
  matrix_23 << 1, 2, 3, 4, 5, 6;//第一行为1 2 3  第二行为4 5 6
  // 输出
  cout << "matrix 2x3 from 1 to 6: \n" << matrix_23 << endl;//输出2 * 3矩阵

  // 用()访问矩阵中的元素
  cout << "print matrix 2x3: " << endl;
  for (int i = 0; i < 2; i++) {
    for (int j = 0; j < 3; j++) cout << matrix_23(i, j) << "\t";
    cout << endl;
  }

  // 矩阵和向量相乘（实际上仍是矩阵和矩阵）
  v_3d << 3, 2, 1;//[3,2,1]
  vd_3d << 4, 5, 6;//[4,5,6]

  // 但是在Eigen里你不能混合两种不同类型的矩阵，像这样是错的
  // Matrix result_wrong_type = matrix_23 * v_3d;
  // error: no type named ‘ReturnType’ in ‘struct Eigen::ScalarBinaryOpTraits >
  // 注意result是double型矩阵，而matrix_23是float型矩阵，因此必须将matrix_23转换成double型矩阵
  // 应该显式转换
  Matrix result = matrix_23.cast() * v_3d;//显式转换
  cout << "[1,2,3;4,5,6]*[3,2,1]=" << result.transpose() << endl;//[1,2,3;4,5,6]*[3,2,1]

  Matrix result2 = matrix_23 * vd_3d;
  cout << "[1,2,3;4,5,6]*[4,5,6]: " << result2.transpose() << endl;//[1,2,3;4,5,6]*[4,5,6]

  // 同样你不能搞错矩阵的维度
  // 试着取消下面的注释，看看Eigen会报什么错 
  // error: static assertion failed: YOU_MIXED_MATRICES_OF_DIFFERENT_SIZES
  // Eigen::Matrix result_wrong_dimension = matrix_23.cast() * v_3d;

  // 一些矩阵运算
  // 四则运算就不演示了，直接用+-*/即可。
  matrix_33 = Matrix3d::Random();      // 随机数矩阵
  cout << "random matrix(3 * 3 随机数矩阵): \n" << matrix_33 << endl;//3 * 3 随机数矩阵
  cout << "transpose(转置): \n" << matrix_33.transpose() << endl;      // 转置
  cout << "sum(各元素和): " << matrix_33.sum() << endl;            // 各元素和
  cout << "trace(迹): " << matrix_33.trace() << endl;          // 迹
  cout << "times 10(数乘): \n" << 10 * matrix_33 << endl;               // 数乘
  cout << "inverse(逆): \n" << matrix_33.inverse() << endl;        // 逆
  cout << "det(行列式): " << matrix_33.determinant() << endl;    // 行列式

  // 特征值
  // 实对称矩阵可以保证对角化成功
  SelfAdjointEigenSolver eigen_solver(matrix_33.transpose() * matrix_33);
  cout << "Eigen values(特征值) = \n" << eigen_solver.eigenvalues() << endl;//特征值
  cout << "Eigen vectors(特征向量) = \n" << eigen_solver.eigenvectors() << endl;//特征向量

  // 解方程
  // 我们求解 matrix_NN * x = v_Nd 这个方程
  // N的大小在前边的宏里定义，它由随机数生成
  // 直接求逆自然是最直接的，但是求逆运算量大

  Matrix matrix_NN
      = MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
  matrix_NN = matrix_NN * matrix_NN.transpose();  // 保证半正定
  Matrix v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);//系数矩阵

  clock_t time_stt = clock(); // 计时
  // 直接求逆
  Matrix x = matrix_NN.inverse() * v_Nd;//v_Nd为Ax=b中的b 即x = A(T)*b
  cout << "time of normal inverse is(求逆所花费的时间)"
       << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;//输出求逆所花费的时间
  cout << "x = " << x.transpose() << endl;//输出x(T)

  // 通常用矩阵分解来求，例如QR分解，速度会快很多
  time_stt = clock();
  x = matrix_NN.colPivHouseholderQr().solve(v_Nd);//colPivHouseholderQr()表示QR分解
  cout << "time of Qr decomposition is(QR分解所花费的时间) "
       << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;//输出QR分解所花费的时间
  cout << "x = " << x.transpose() << endl;//输出x(T)

  // 对于正定矩阵，还可以用cholesky分解来解方程
  time_stt = clock();
  x = matrix_NN.ldlt().solve(v_Nd);//ldlt()表示cholesky分解
  cout << "time of ldlt decomposition is(cholesky分解所花费的时间)"
       << 1000 * (clock() - time_stt) / (double) CLOCKS_PER_SEC << "ms" << endl;//输出cholesky分解所花费的时间
  cout << "x = " << x.transpose() << endl;//输出x(T)
  return 0;
}

CmakeLists文件：

cmake_minimum_required(VERSION 2.8)
project(useEigen)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")

# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(eigenMatrix eigenMatrix.cpp)

eigenGeometry.cpp

#include 
#include 

using namespace std;

#include 
#include 

using namespace Eigen;

// 本程序演示了 Eigen 几何模块的使用方法

int main(int argc, char **argv) {

  // Eigen/Geometry 模块提供了各种旋转和平移的表示
  // 3D 旋转矩阵直接使用 Matrix3d 或 Matrix3f
  Matrix3d rotation_matrix = Matrix3d::Identity();
  // 旋转向量使用 AngleAxis, 它底层不直接是Matrix，但运算可以当作矩阵（因为重载了运算符）
  AngleAxisd rotation_vector(M_PI / 4, Vector3d(0, 0, 1));     //沿 Z 轴旋转 45 度 
  cout.precision(3);//输出3位有效数字
  cout << "rotation matrix =\n" << rotation_vector.matrix() << endl;   //用matrix()转换成矩阵 可以想象原来坐标系旋转45度后变成了根号2那个位置
  // 也可以直接赋值
  rotation_matrix = rotation_vector.toRotationMatrix();
  // 用 AngleAxis 可以进行坐标变换
  Vector3d v(1, 0, 0);//[1,0,0]
  Vector3d v_rotated = rotation_vector * v;//[0.707,-0.707,0.707;0.707,0.707;0,0,1] * [1,0,0]
  cout << "(1,0,0) after rotation (by angle axis) = " << v_rotated.transpose() << endl;//输出[0.707,-0.707,0.707;0.707,0.707;0,0,1] * [1,0,0]
  // 或者用旋转矩阵
  v_rotated = rotation_matrix * v;//rotation_matrix * [1,0,0]
  cout << "(1,0,0) after rotation (by matrix) = " << v_rotated.transpose() << endl;//输出rotation_matrix * [1,0,0]

  // 欧拉角: 可以将旋转矩阵直接转换成欧拉角
  Vector3d euler_angles = rotation_matrix.eulerAngles(2, 1, 0); // ZYX顺序，即yaw-pitch-roll顺序
  //[0.707,-0.707,0.707;0.707,0.707;0,0,1]的欧拉角为PI/4
  cout << "yaw pitch roll = " << euler_angles.transpose() << endl;//输出欧拉角为PI/4 [0.785,-0,0]

  // 欧氏变换矩阵使用 Eigen::Isometry
  Isometry3d T = Isometry3d::Identity();                // 虽然称为3d，实质上是4＊4的矩阵
  T.rotate(rotation_vector);                                     // 按照rotation_vector进行旋转
  T.pretranslate(Vector3d(1, 3, 4));                     // 把平移向量设成(1,3,4)
  // t(0,3) = 1;t(1,3) = 3; t(2,3) = 4;        // 把平移向量设成(1,3,4)
  cout << "Transform matrix = \n" << T.matrix() << endl;

  // 用变换矩阵进行坐标变换
  Vector3d v_transformed = T * v;                              // 相当于R*v+t
  cout << "v tranformed = " << v_transformed.transpose() << endl;//[1,0,0] --> [0.707,0.707,0] 
  // [0.707,0.707,0] + [1,3,4] = [1.707,3.707,4] -->三位有效数字 [1.71,3.71,4] <-- R*v+t

  // 对于仿射和射影变换，使用 Eigen::Affine3d 和 Eigen::Projective3d 即可，略

  // 四元数
  // 可以直接把AngleAxis赋值给四元数，反之亦然
  Quaterniond q = Quaterniond(rotation_vector);
  cout << "quaternion from rotation vector = " << q.coeffs().transpose()
       << endl;   // 请注意coeffs的顺序是(x,y,z,w),w为实部，前三者为虚部
  // 也可以把旋转矩阵赋给它
  q = Quaterniond(rotation_matrix);
  cout << "quaternion from rotation matrix = " << q.coeffs().transpose() << endl;
  // 使用四元数旋转一个向量，使用重载的乘法即可
  v_rotated = q * v; // 注意数学上是qvq^{-1}
  cout << "(1,0,0) after rotation = " << v_rotated.transpose() << endl;//(1,0,0) after rotation = 0.707 0.707 0
  // 用常规向量乘法表示，则应该如下计算
  cout << "should be equal to " << (q * Quaterniond(0, 1, 0, 0) * q.inverse()).coeffs().transpose() << endl;
  //should be equal to 0.707 0.707  0  0

  return 0;
}

CmakeLists文件：

​
cmake_minimum_required( VERSION 2.8 )
project( geometry )

# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )

add_executable(eigenGeometry eigenGeometry.cpp)

​

coordinateTransform.cpp

#include 
#include 
#include 
#include //Eigen核心模块
#include //Eigen几何模块

using namespace std;
using namespace Eigen;

//坐标变换 
//已知q1，t1，p1以及q2，t2，求解q2
int main(int argc, char** argv) {
  Quaterniond q1(0.35, 0.2, 0.3, 0.1), q2(-0.5, 0.4, -0.1, 0.2); //位姿，以Tcw形式存储
  q1.normalize();//将q1归一化
  q2.normalize();//将q2归一化
  Vector3d t1(0.3, 0.1, 0.1), t2(-0.1, 0.5, 0.3);//平移向量
  Vector3d p1(0.5, 0, 0.2);

  Isometry3d T1w(q1), T2w(q2);
  T1w.pretranslate(t1);
  T2w.pretranslate(t2);

  Vector3d p2 = T2w * T1w.inverse() * p1;
  cout << endl << p2.transpose() << endl;
  return 0;
}

plotTrajectory.cpp

#include 
#include //Eigen核心模块
#include 

// 本例演示了如何画出一个预先存储的轨迹

using namespace std;
using namespace Eigen;
//以Twr格式存储位姿
//该txt文件中每行的格式为：time, tx, ty, tx, qx, qy, qz, qw
// path to trajectory file
string trajectory_file = "/home/liqiang/slambook2/ch3/examples/trajectory.txt";//相机的轨迹文件
//string trajectory_file = "../trajectory.txt";//或者使用下面这种表达方式
void DrawTrajectory(vector>);
//Eigen::aligned_allocator表示内存管理方法
//向量类容器中的元素是Isometry3d，内存管理方法是Eigen::aligned_allocator

int main(int argc, char **argv) {

  vector> poses;
  ifstream fin(trajectory_file);
  if (!fin)//如果不能打开文件
  {
    cout << "cannot find trajectory file at " << trajectory_file << endl;//输出不能读取文件
    return 1;
  }

  while (!fin.eof()) //如果此时fin并不是end of file，那么执行以下内容
  {
    double time, tx, ty, tz, qx, qy, qz, qw;//后面四个为四元数，最后一个为实部
    fin >> time >> tx >> ty >> tz >> qx >> qy >> qz >> qw;
    Isometry3d Twr(Quaterniond(qw, qx, qy, qz));//Quaterniond 四元数
    Twr.pretranslate(Vector3d(tx, ty, tz));
    poses.push_back(Twr);
  }
  cout << "read total " << poses.size() << " pose entries" << endl;//输出读取到多少个位姿

  // draw trajectory in pangolin
  DrawTrajectory(poses);  //调用DrawTrajectory()函数进行绘图
  return 0;
}

/*******************************************************************************************/
void DrawTrajectory(vector> poses) {
  // create pangolin window and plot the trajectory（创建pangolin窗口和绘制轨迹）
  pangolin::CreateWindowAndBind("Trajectory Viewer", 1024, 768);//分别表示窗口名、窗口宽度和窗口高度
  glEnable(GL_DEPTH_TEST);//启用深度渲染，当需要显示3D模型时需要打开，根据目标的远近自动隐藏被遮挡的模型
  glEnable(GL_BLEND); //表示窗口使用颜色混合模式，让物体显示半透明效果
  glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);//GL_SRC_ALPHA表示使用源颜色的alpha值作为权重因子，GL_ONE_MINUS_SRC_ALPHA表示用1.0-源颜色的alpha值作为权重因子

//创建一个观察相机视图
  pangolin::OpenGlRenderState s_cam(
    pangolin::ProjectionMatrix(1024, 768, 500, 500, 512, 389, 0.1, 1000),
    pangolin::ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)
  );
//ProjectionMatrix中各参数依次为图像宽度=1024、图像高度=768、fx=500、fy=500、cx=512、cy=389、最近距离=0.1、最远距离=1000
//ModelViewLookAt中各参数依次为相机的三维位置（0，-0.1，-1.8），观看视点的三维位置（0，0，0）和设置相机各轴的正方向（0，-1，0），右下前为（0，0，0），右上前为（0，-1，0）
//比如，ModelViewLookAt(0, -0.1, -1.8, 0, 0, 0, 0.0, -1.0, 0.0)表示相机在(0, -0.1, -1.8)位置处观看视点(0, 0, 0)，并设置相机XYZ轴正方向为（0，-1，0），即右上前


//创建交互视图，用于显示上一步相机所观测到的内容
  pangolin::View &d_cam = pangolin::CreateDisplay()
    .SetBounds(0.0, 1.0, 0.0, 1.0, -1024.0f / 768.0f)
    .SetHandler(new pangolin::Handler3D(s_cam));
//SetBounds()内的前4个参数分别表示交互视图的大小，均为相对值，范围在0.0至1.0之间
    //第1个参数表示bottom，即为视图最下面在整个窗口中的位置
    //第2个参数为top，即为视图最上面在整个窗口中的位置
    //第3个参数为left，即视图最左边在整个窗口中的位置
    //第4个参数为right，即为视图最右边在整个窗口中的位置
    //第5个参数为aspect，表示横纵比
    
  while (pangolin::ShouldQuit() == false) //ShouldQuit()检测是否关闭OpenGL窗口，如果没有关闭则执行
  {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);//清空颜色和深度缓存，这样每次都会刷新显示，不至于前后帧的颜色信息相互干扰
    d_cam.Activate(s_cam);//激活显示，并设置状态矩阵
    glClearColor(1.0f, 1.0f, 1.0f, 1.0f);//将背景显示为白色
    glLineWidth(1);//设置线宽
    for (size_t i = 0; i < poses.size(); i++) {
      // 画每个位姿的三个坐标轴
      Vector3d Ow = poses[i].translation();//相机坐标系的坐标原点(0, 0, 0)在世界系下的坐标
      Vector3d Xw = poses[i] * (0.1 * Vector3d(1, 0, 0)); //相机坐标系中的点(0.1, 0, 0)在世界坐标系下的坐标
      Vector3d Yw = poses[i] * (0.1 * Vector3d(0, 1, 0)); //相机坐标系中的点(0, 0.1, 0)在世界坐标系下的坐标
      Vector3d Zw = poses[i] * (0.1 * Vector3d(0, 0, 1)); //相机坐标系中的点(0, 0, 0.1)在世界坐标系下的坐标
      //绘制直线OA、OB和OC分别表示该时刻相机坐标系的X轴、Y轴和Z轴
      glBegin(GL_LINES);
      glColor3f(1.0, 0.0, 0.0);//X轴用红色表示
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Xw[0], Xw[1], Xw[2]);
      glColor3f(0.0, 1.0, 0.0);//Y轴用绿色表示
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Yw[0], Yw[1], Yw[2]);
      glColor3f(0.0, 0.0, 1.0);//Z轴用蓝色表示
      glVertex3d(Ow[0], Ow[1], Ow[2]);
      glVertex3d(Zw[0], Zw[1], Zw[2]);
      glEnd();//对应于glBegin()
    }
    // 画出连线p1p2
    for (size_t i = 0; i < poses.size(); i++) {
      glColor3f(0.0, 0.0, 0.0);//设置直线颜色为黑色
      glBegin(GL_LINES);//绘制直线p1p2
      glLineWidth(2); //线宽设置为2
      auto p1 = poses[i], p2 = poses[i + 1];
      glVertex3d(p1.translation()[0], p1.translation()[1], p1.translation()[2]);
      glVertex3d(p2.translation()[0], p2.translation()[1], p2.translation()[2]);
      glEnd();
    }
    pangolin::FinishFrame();//执行后期渲染、事件处理和帧交换，按照前面的设置进行最终的显示
    usleep(5000);   // sleep 5 ms
  }
}

include_directories("/usr/include/eigen3")
add_executable(coordinateTransform coordinateTransform.cpp)

find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})
add_executable(plotTrajectory plotTrajectory.cpp)
target_link_libraries(plotTrajectory ${Pangolin_LIBRARIES})

执行效果：

visualizeGeometry.cpp

#include 
#include 

using namespace std;

#include //Eigen核心模块
#include //Eigen几何模块

using namespace Eigen;

#include 

struct RotationMatrix 
{
  Matrix3d matrix = Matrix3d::Identity();//Matrix3d::Identity()表示3*3单位阵
};

//重载结构体RotationMatrix的输出流运算符<<
ostream &operator<<(ostream &out, const RotationMatrix &r) {
  out.setf(ios::fixed); //fixed表示用正常的记数方法显示浮点数
  Matrix3d matrix = r.matrix;
  out << '=';
  //先out.setf(ios::fixed)，后setprecision(2)，效果为保留小数点后两位
  out << "[" << setprecision(2) << matrix(0, 0) << "," << matrix(0, 1) << "," << matrix(0, 2) << "],"
      << "[" << matrix(1, 0) << "," << matrix(1, 1) << "," << matrix(1, 2) << "],"
      << "[" << matrix(2, 0) << "," << matrix(2, 1) << "," << matrix(2, 2) << "]";
  return out;
}
//重载结构体RotationMatrix的输入流运算符>>
istream &operator>>(istream &in, RotationMatrix &r) {
  return in;
}

struct TranslationVector {
  Vector3d trans = Vector3d(0, 0, 0);
};

//重载结构体TranslationVector的输出流运算符<<
ostream &operator<<(ostream &out, const TranslationVector &t) {
  out << "=[" << t.trans(0) << ',' << t.trans(1) << ',' << t.trans(2) << "]";
  return out;
}

//重载结构体TranslationVector的输入流运算符>>
istream &operator>>(istream &in, TranslationVector &t) {
  return in;
}

struct QuaternionDraw {
  Quaterniond q;
};

//重载结构体QuaternionDraw的输出流运算符<<
ostream &operator<<(ostream &out, const QuaternionDraw quat) {
  auto c = quat.q.coeffs();
  out << "=[" << c[0] << "," << c[1] << "," << c[2] << "," << c[3] << "]";
  return out;
}

//重载结构体QuaternionDraw的输出流运算符<<
istream &operator>>(istream &in, const QuaternionDraw quat) {
  return in;
}

int main(int argc, char **argv) 
{
  //创建pangolin窗口
  pangolin::CreateWindowAndBind("visualize geometry", 1000, 600);//分别表示窗口名visualize geometry、窗口宽度=1000和窗口高度=600
  glEnable(GL_DEPTH_TEST); //启用深度渲染，当需要显示3D模型时需要打开，根据目标的远近自动隐藏被遮挡的模型
  //创建一个观察相机视图，包括投影矩阵和相机视角
  pangolin::OpenGlRenderState s_cam(
    pangolin::ProjectionMatrix(1000, 600, 420, 420, 500, 300, 0.1, 1000),
    pangolin::ModelViewLookAt(3, 3, 3, 0, 0, 0, pangolin::AxisY)
  );
  //ProjectionMatrix()中各参数依次为图像宽度=1000、图像高度=600、fx=420、fy=420、cx=500、cy=300、最近距离=0.1和最远距离=1000
  //ModelViewLookAt()中各参数为相机位置，被观察点位置和相机哪个轴朝上
  //比如，ModelViewLookAt(3, 3, 3, 0, 0, 0, pangolin::AxisY)表示相机在(3, 3, 3)位置处观看视点(0, 0, 0)
  
  const int UI_WIDTH = 500;//用户界面所占宽度，从左边算起
  //创建交互视图，用于显示上一步相机所观测到的内容
  pangolin::View &d_cam = pangolin::CreateDisplay().
    SetBounds(0.0, 1.0, pangolin::Attach::Pix(UI_WIDTH), 1.0, -1000.0f / 600.0f).
    SetHandler(new pangolin::Handler3D(s_cam));
  //SetBounds()内的前4个参数分别表示交互视图的大小，均为相对值，范围在0.0至1.0之间
  //第1个参数表示bottom，即为视图最下面在整个窗口中的位置
  //第2个参数为top，即为视图最上面在整个窗口中的位置
  //第3个参数为left，即视图最左边在整个窗口中的位置
  //第4个参数为right，即为视图最右边在整个窗口中的位置
  //第5个参数为aspect，表示横纵比
  
  //设置UI界面
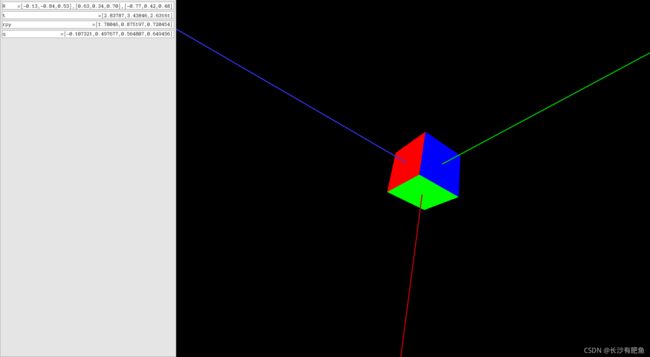
  pangolin::Var rotation_matrix("ui.R", RotationMatrix());//显示旋转矩阵
  pangolin::Var translation_vector("ui.t", TranslationVector());//显示平移向量
  pangolin::Var euler_angles("ui.rpy", TranslationVector());//显示欧拉角
  pangolin::Var quaternion("ui.q", QuaternionDraw());//显示四元数
  pangolin::CreatePanel("ui").SetBounds(0.0, 1.0, 0.0, pangolin::Attach::Pix(UI_WIDTH));//设置用户界面的大小

  while (!pangolin::ShouldQuit()) //如果没有关闭OpenGL窗口，则执行
  {
    glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); //清空颜色和深度缓存，使每一帧之间互不干扰

    d_cam.Activate(s_cam);//激活显示，设置相机状态

    pangolin::OpenGlMatrix matrix = s_cam.GetModelViewMatrix(); //将模型可视化矩阵赋值给matrix
    Matrix m = matrix;
    
    //赋值旋转矩阵
    RotationMatrix R;
    for (int i = 0; i < 3; i++)
      for (int j = 0; j < 3; j++)
        R.matrix(i, j) = m(j, i);
    rotation_matrix = R;

    //赋值平移向量
    TranslationVector t;
    t.trans = Vector3d(m(0, 3), m(1, 3), m(2, 3));
    t.trans = -R.matrix * t.trans;
    translation_vector = t;
    
    //赋值欧拉角向量
    TranslationVector euler;
    euler.trans = R.matrix.eulerAngles(2, 1, 0);
    euler_angles = euler;
    
    //赋值四元数
    QuaternionDraw quat;
    quat.q = Quaterniond(R.matrix);
    quaternion = quat;

    glColor3f(1.0, 1.0, 1.0);//设置背景颜色为白色
   
    //绘制立方体
    pangolin::glDrawColouredCube();
    // draw the original axis (绘制坐标系)
    glLineWidth(3);
    glColor3f(0.8f, 0.f, 0.f); //设置X轴为红色
    glBegin(GL_LINES);
    glVertex3f(0, 0, 0);
    glVertex3f(10, 0, 0);
    glColor3f(0.f, 0.8f, 0.f);//设置Y轴为绿色
    glVertex3f(0, 0, 0);
    glVertex3f(0, 10, 0);
    glColor3f(0.2f, 0.2f, 1.f); //设置Z轴颜色
    glVertex3f(0, 0, 0);
    glVertex3f(0, 0, 10);
    glEnd();

    pangolin::FinishFrame();//执行后期渲染、事件处理和帧交换，按照前面的设置进行最终的显示
  }
}

CmakeLists文件：

cmake_minimum_required( VERSION 2.8 )
project( visualizeGeometry )

set(CMAKE_CXX_FLAGS "-std=c++11")

# 添加Eigen头文件
include_directories( "/usr/include/eigen3" )

# 添加Pangolin依赖
find_package( Pangolin )
include_directories( ${Pangolin_INCLUDE_DIRS} )

add_executable( visualizeGeometry visualizeGeometry.cpp )
target_link_libraries( visualizeGeometry ${Pangolin_LIBRARIES} )

执行效果：

课后习题

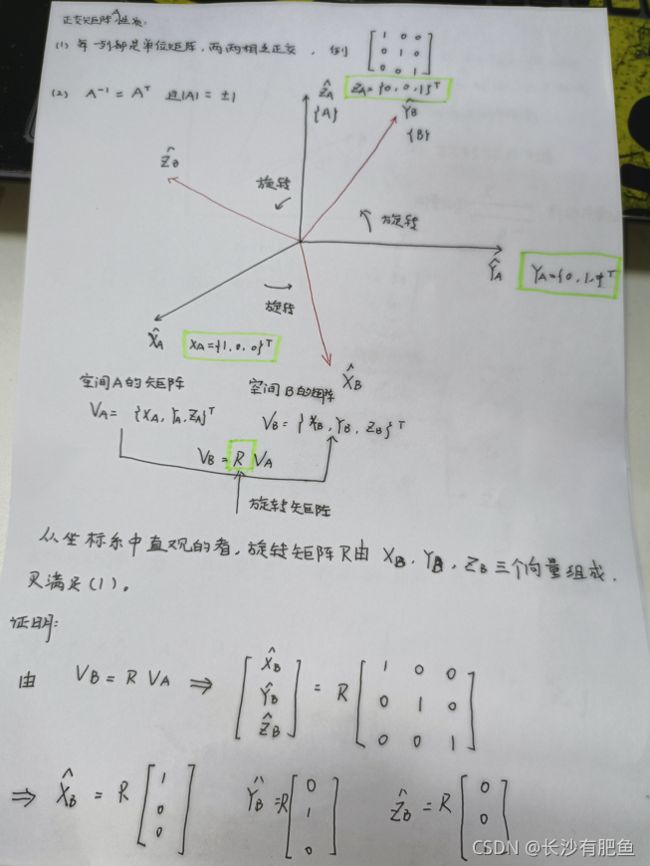
1. 验证旋转矩阵是正交矩阵。

参考链接：
旋转矩阵(Rotate Matrix)的性质分析 - caster99 - 博客园

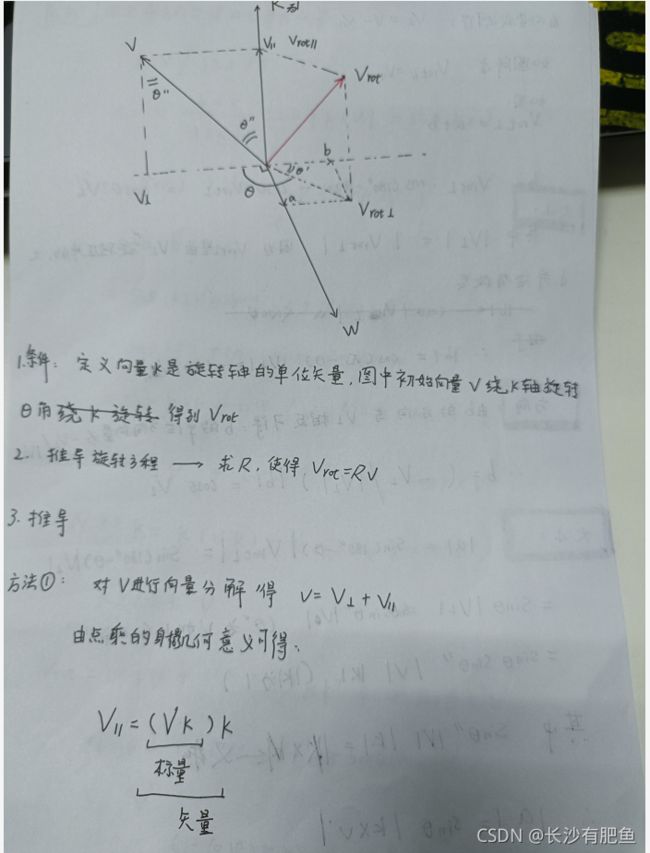
2. * 寻找罗德里格斯公式的推导过程并理解它。

 参考链接：

https://blog.csdn.net/qq_41665685/article/details/106139331

3. 验证四元数旋转某个点后,结果是一个虚四元数(实部为零),所以仍然对应到一个三维空间点(式 3.34)

参考链接： 四元数旋转运算过程_gxsHeeN的博客-CSDN博客_四元数旋转公式

4. 画表总结旋转矩阵、轴角、欧拉角、四元数的转换关系。

这里不画了。。

5. 假设我有一个大的 Eigen 矩阵,我想把它的左上角 3 × 3 的块取出来,然后赋值为I3×3 。请编程实现。

matrix_extraction.cpp

#include

//包含Eigen头文件
#include//Eigen核心模块
#include//Eigen几何模块

#define MATRIX_SIZE 30//定义矩阵的大小
using namespace std;

int main(int argc,char **argv)
{
    //设置输出小数点后3位
    cout.precision(3);
    Eigen::Matrix matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE);//生成随机数矩阵
    Eigen::Matrixmatrix_3d1 = Eigen::MatrixXd::Random(3,3);//3x3矩阵变量
    Eigen::Matrix3d matrix_3d = Eigen::Matrix3d::Random();//两种方式都可以
/*方法1：循环遍历矩阵的三行三列   */
    for(int i = 0;i < 3; i ++)
    {
        for(int j = 0 ;j < 3;j++)
        {
            matrix_3d(i,j) = matrix_NN(i,j);
            cout<

cmake_minimum_required(VERSION 2.8)
project(homework)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")

# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(matrix_extraction matrix_extraction.cpp)

执行结果：
 

x_extraction 
0.68 0.0259 -0.523 
-0.211 0.678 0.941 
0.566 0.225 0.804 
赋值后的矩阵为:
1 0 0
0 1 0
0 0 1
提取出来的矩阵块为:
  0.68 0.0259 -0.523
-0.211  0.678  0.941
 0.566  0.225  0.804
赋值后的矩阵为:
1 0 0
0 1 0
0 0 1

转载于：灰色的石头 - 博客园

6. * 一般线程方程 Ax = b 有哪几种做法?你能在 Eigen 中实现吗?

axb.cpp

#include
#include
#include 
#include 
/*线性方程组Ax = b的解法(直接法（1,2,3,4,5）+迭代法(6))其中只有2 3方法不要求方程组个数与变量个数相等*/

//包含Eigen头文件
//#include 
#include
#include
#include 

//下面这两个宏的数值一样的时候 方法1 4 5 6才能正常工作
#define MATRIX_SIZE 3   //方程组个数
#define MATRIX_SIZE_ 3  //变量个数
//using namespace std;
typedef  Eigen::Matrix  Mat_A;
typedef  Eigen::Matrix            Mat_B;

//Jacobi迭代法的一步求和计算
double Jacobi_sum(Mat_A   &A,Mat_B   &x_k,int i);

//迭代不收敛的话 解向量是0
Mat_B Jacobi(Mat_A   &A,Mat_B   &b,  int &iteration_num, double &accuracy );

int main(int argc,char **argv)
{
    //设置输出小数点后3位
    std::cout.precision(3);
    //设置变量
    Eigen::Matrix matrix_NN = Eigen::MatrixXd::Random(MATRIX_SIZE,MATRIX_SIZE_);//随机数矩阵
    Eigen::Matrix v_Nd = Eigen::MatrixXd::Random(MATRIX_SIZE,1);//解向量

    //测试用例
    matrix_NN << 10,3,1,2,-10,3,1,3,10;//测试所用矩阵
    v_Nd <<14,-5,14;//解向量

    //设置解变量
    Eigen::Matrixx;//Ax=b中的b

    //时间变量
    clock_t tim_stt = clock();

/*1、求逆法	很可能没有解 仅仅针对方阵才能计算*/
#if (MATRIX_SIZE == MATRIX_SIZE_)
    x = matrix_NN.inverse() * v_Nd;//x=A(T)*b
    std::cout<<"直接法所用时间和解为："<< 1000*(clock() - tim_stt)/(double)CLOCKS_PER_SEC
        <<"MS"<< std::endl << x.transpose() << std::endl;
#else
    std::cout<<"直接法不能解!(提示:直接法中方程组的个数必须与变量个数相同，需要设置MATRIX_SIZE == MATRIX_SIZE_)"<es(B);
    EV = es.eigenvalues();
//    cout<<"迭代矩阵特征值为:"< __complex_abs(EV(index)) )?maxev:(__complex_abs(EV(index)));
    }
    std::cout<< "Jacobi迭代矩阵的谱半径为："<< maxev<= 1){
        std::cout<<"Jacobi迭代算法不收敛！"< R )
                    R = temp;
            }

            //判断进度是否达到精度要求 达到进度要求后 自动退出
            if( R < accuracy ){
                std::cout <<"Jacobi迭代算法迭代"<< k << "次达到精度要求."<< std::endl;
                isFlag = 1;
                break;
            }

            //清零R，交换迭代解
            R = 0;
            x_k = x_k1;
        }
        if( !isFlag )
            std::cout << std::endl <<"迭代"<

cmake_minimum_required(VERSION 2.8)
project(homework1)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")

# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(axb axb.cpp)

执行结果:

直接法所用时间和解为：0.022MS
1 1 1
QR分解所用时间和解为：0.005MS
1 1 1
最小二乘法所用时间和解为:0.001MS
1 1 1
LU分解方法所用时间和解为:0.003MS
1 1 1
Cholesky 分解方法所用时间和解为:0.001MS
    1.4 -0.0472   0.103

欢迎进入Jacobi迭代算法！
Jacobi迭代矩阵的谱半径为：0.387
Jacobi迭代算法谱半径小于1,该算法收敛
Jacobi迭代法迭代次数和精度： 
10 0.01
Jacobi迭代算法迭代6次达到精度要求.
Jacobi 迭代法所用时间和解为:0.035MS
0.998     1 0.998

转载于：视觉slam十四讲课后习题ch3-6 - 灰色的石头 - 博客园