数字图像处理_05_(图像锐化与边缘检测——Premittt算子、Roberts算子、Sobel算子、Scharr算子、Laplacian算子、LoG算子、Canny算子)
本章将介绍在图像处理中常用到的几个卷积核(算子)实现图像的边缘检测和锐化操作,有Premittt算子、Roberts算子、Sobel算子、Scharr算子、Laplacian算子、LoG算子、Canny算子。
1.Premittt算子
介绍:Prewitt算子是一种一阶微分算子的边缘检测,利用像素点上下、左右邻点的灰度差,在边缘处达到极值检测边缘,去掉部分伪边缘,对噪声具有平滑作用 。
原理:其原理是在图像空间利用两个方向模板与图像进行邻域卷积来完成的,这两个方向模板一个检测水平边缘,一个检测垂直边缘。
水平梯度方向的卷积核3 * 3模板:
K x = [ − 1 0 1 − 1 0 1 − 1 0 1 ] K_x= \left[ \begin{array}{ccc} -1&0&1\\ - 1&0&1\\ -1&0&1\\ \end{array} \right] Kx=⎣⎡−1−1−1000111⎦⎤
竖直梯度方向的卷积核3 * 3模板:
K y = [ − 1 − 1 − 1 0 0 0 1 1 1 ] K_y= \left[ \begin{array}{ccc} -1&-1&-1\\ 0&0&0\\ 1&1&1\\ \end{array} \right] Ky=⎣⎡−101−101−101⎦⎤
水平梯度方向代码:
kx = np.array([
[-1,0,1],
[-1,0,1],
[-1,0,1],
],dtype=np.float64)
img_x = cv.filter2D(img,cv.CV_64F,kx)
show(np.abs(img_x))
ky = np.array([
[-1,-1,-1],
[0,0,0],
[1,1,1]
],dtype=np.float64)
img_y = cv.filter2D(img,cv.CV_64F,ky)
show(np.abs(img_y))
输出图像为:

两者融合则为边缘的检测:
融合有两种方式:
1: K x y = ∣ K x ∣ + ∣ K y ∣ K_{xy}=|K_x|+|K_y| Kxy=∣Kx∣+∣Ky∣
2: K x y = K x 2 + K y 2 K_{xy}=\sqrt{K_x^2+K_y^2} Kxy=Kx2+Ky2
img_xy1= np.abs(img_x)+np.abs(img_y)
img_xy2 = np.power(img_x**2+img_y**2,0.5)
show(np.hstack([img_xy1,img_xy2]))
cv.imwrite('test/kxy.jpg',np.hstack([img_xy1,img_xy2]))
2.Roberts算子
介绍:Roberts算子,又称罗伯茨算子,是一种最简单的算子,是一种利用局部差分算子寻找边缘的算子。检测垂直边缘的效果好于斜向边缘,定位精度高,对噪声敏感,无法抑制噪声的影响。
原理:他采用对角线方向相邻两象素之差近似梯度幅值检测边缘。
卷积核2 * 2模板1:
K 1 = [ − 1 0 0 1 ] K_1= \left[ \begin{array}{ccc} -1&0\\ 0&1\\ \end{array} \right] K1=[−1001]
卷积核2 * 2模板2:
K 2 = [ 0 − 1 1 0 ] K_2= \left[ \begin{array}{ccc} 0&-1\\ 1&0\\ \end{array} \right] K2=[01−10]
代码实现如下:
k_rob1 = np.array([
[-1,0],
[0,1]
],dtype=np.float64)
img_rob1 = cv.filter2D(img,cv.CV_64F,k_rob1)
k_rob2 = np.array([
[0,-1],
[1,0]
],dtype=np.float64)
img_rob2 = cv.filter2D(img,cv.CV_64F,k_rob2)
img_xy=np.abs(img_rob1)+np.abs(img_rob2)
img_xy2=np.sqrt(img_rob1**2+img_rob2**2)
show(np.hstack([img_xy,img_xy2]))
3.Sobel算子
介绍:在边缘检测中,常用的一种模板是Sobel 算子。Sobel 算子有两个,一个是检测水平边缘的 ;另一个是检测垂直边缘的 。与Prewitt算子相比,Sobel算子对于象素的位置的影响做了加权,可以降低边缘模糊程度,因此效果更好。
原理:Sobel算子是把图像中每个像素的上下左右四领域的灰度值加权差,在边缘处达到极值从而检测边缘。
水平梯度方向的卷积核3 * 3模板:
K x = [ − 1 0 1 − 2 0 2 − 1 0 1 ] K_x= \left[ \begin{array}{ccc} -1&0&1\\ - 2&0&2\\ -1&0&1\\ \end{array} \right] Kx=⎣⎡−1−2−1000121⎦⎤
竖直梯度方向的卷积核3 * 3模板:
K y = [ − 1 − 2 − 1 0 0 0 1 2 1 ] K_y= \left[ \begin{array}{ccc} -1&-2&-1\\ 0&0&0\\ 1&2&1\\ \end{array} \right] Ky=⎣⎡−101−202−101⎦⎤
自己实现代码:
kx = np.array([
[-1,0,1],
[-2,0,2],
[-1,0,1],
],dtype=np.float64)
img_x = cv.filter2D(img,cv.CV_64F,kx)
ky=np.array([
[-1,-2,-1],
[0,0,0],
[1,2,1]
])
img_y =cv.filter2D(img,cv.CV_64F,ky)
img_xy1=np.abs(img_x)+np.abs(img_y)
img_xy2=np.sqrt(img_x**2+img_y**2)
show(np.hstack([img_xy1,img_xy2]))
cv.imwrite('test/Sobel1.jpg',np.hstack([img_xy1,img_xy2]))
输出图像为: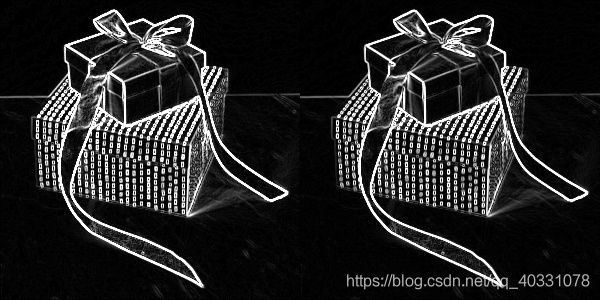
OpenCV自带有Sobel(原图像,数据类型,x梯度方向,y梯度方向),代码实现为:
img_sobel_x = cv.Sobel(img,cv.CV_16S,1,0)
img_sobel_y = cv.Sobel(img,cv.CV_16S,0,1)
img_sobel1=np.abs(img_sobel_x)+np.abs(img_sobel_y)
img_sobel2=np.sqrt(img_sobel_x**2+img_sobel_y**2)
show(img_sobel1)
#show(np.stack([img_sobel1,img_sobel2]))
cv.imwrite('test/Sobel2.jpg',img_sobel1)
4.Scharr算子
介绍:Sobel算子可以有效的提取图像边缘,但是对图像中较弱的边缘提取效果较差。因此为了能够有效的提取出较弱的边缘,需要将像素值间的差距增大,因此引入Scharr算子。
原理:Scharr算子是把图像中每个像素的上下左右四领域的灰度值加权差,在边缘处达到极值从而检测边缘。
水平梯度方向的卷积核3 * 3模板:
K x = [ − 3 0 3 − 10 0 10 − 3 0 3 ] K_x= \left[ \begin{array}{ccc} -3&0&3\\ - 10&0&10\\ -3&0&3\\ \end{array} \right] Kx=⎣⎡−3−10−30003103⎦⎤
竖直梯度方向的卷积核3 * 3模板:
K y = [ − 3 − 10 − 3 0 0 0 3 10 3 ] K_y= \left[ \begin{array}{ccc} -3&-10&-3\\ 0&0&0\\ 3&10&3\\ \end{array} \right] Ky=⎣⎡−303−10010−303⎦⎤
OpenCV自带有Scharr(原图像,数据类型,x梯度方向,y梯度方向),代码实现为
img_x = cv.Scharr(img,cv.CV_64F,1,0)
img_y = cv.Scharr(img,cv.CV_64F,0,1)
img_Scharr = np.power(img_x**2+img_y**2,0.5)
img_Scharr = img_Scharr.clip(0,255)
show(img_Scharr)
cv.imwrite('test/img_Scharr.jpg',img_Scharr)
5.Laplacian算子
介绍:Laplacian 算子是n维欧几里德空间中的一个二阶微分算子,定义为梯度grad的散度div。可使用运算模板来运算这定理定律。
原理:函数的Laplacian 算子也是该函数的黑塞矩阵的迹,可以证明,它具有各向同性,即与坐标轴方向无关,坐标轴旋转后梯度结果不变。
卷积核3 * 3模板1:
K 1 = [ 0 1 0 1 − 4 1 0 1 0 ] K_1= \left[ \begin{array}{ccc} 0&1&0\\ 1&-4&1\\ 0&1&0\\ \end{array} \right] K1=⎣⎡0101−41010⎦⎤
卷积核3 * 3模板2:
K 2 = [ 1 1 1 1 − 8 1 1 1 1 ] K_2= \left[ \begin{array}{ccc} 1&1&1\\ 1&-8&1\\ 1&1&1\\ \end{array} \right] K2=⎣⎡1111−81111⎦⎤
OpenCV提供了Laplacian(原图像,数据类型)
img_lap=cv.Laplacian(img,cv.CV_64F)
show(np.hstack([img,np.abs(img_lap)]))
cv.imwrite('test/img_Lap.jpg',np.hstack([img,np.abs(img_lap)]))
6.LoG算子
介绍:也就是 Laplace of Gaussian function(高斯拉普拉斯函数)。常用于数字图像的边缘提取和二值化。LoG 算子源于D.Marr计算视觉理论中提出的边缘提取思想, 即首先对原始图像进行最佳平滑处理, 最大程度地抑制噪声, 再对平滑后的图像求取边缘。
原理:在Laplacian 算子基础之上增加了高斯模糊。
img_GBlur=cv.GaussianBlur(img,(3,3),1)
img_LoG = cv.Laplacian(img_GBlur,cv.CV_64F)
show(np.hstack([img,np.abs(img_lap),np.abs(img_LoG )]))
cv.imwrite('test/img_Lap.jpg',np.hstack([img,np.abs(img_lap),np.abs(img_LoG )]))
6.Canny算子(了解)
Canny的目标是找到一个最优的边缘检测算法,最优边缘检测的含义是:
- 好的检测- 算法能够尽可能多地标识出图像中的实际边缘。
- 好的定位- 标识出的边缘要与实际图像中的实际边缘尽可能接近。
- 最小响应-
图像中的边缘只能标识一次,并且可能存在的图像噪声不应标识为边缘。
OpenCV提供了Canny(原图像,阈值1,阈值2)
img_Canny=cv.Canny(img,2,200)
show(img_Canny)
cv.imwrite('test/img_Canny.jpg',img_Canny)







