pytorch深度学习实践3——多分类问题,卷积神经网络CNN
多分类问题Softmax Classifier分类器
全连接网络:用线性层将网络连接在一起

softmax数学原理:

loss函数实现方法:
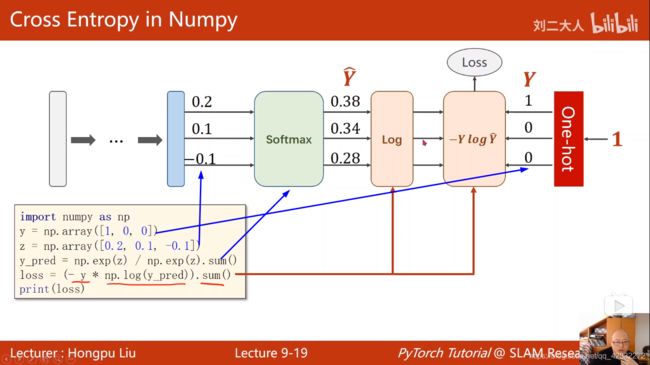
import numpy as np
y = np.array([1,0,0])
z = np.array([0.2,0.1,-0.1])
y_pred = np.exp(z)/np.exp(z).sum()
loss = (-y*np.log(y_pred)).sum()
print(loss)
import torch
y = torch.LongTensor([0])
z = torch.Tensor([[0.2,0.1,-0.1]])
criterion = torch.nn.CrossEntropyLoss()
loss = criterion(z,y)
print(loss)
import torch
criterion = torch.nn.CrossEntropyLoss()
Y = torch.LongTensor([2,0,1])
Y_pred1 = torch.Tensor([[0.1,0.2,0.9],
[1.1,0.1,0.2],
[0.2,2.1,0.1]])
Y_pred2 = torch.Tensor([[0.8,0.2,0.3],
[0.2,0.3,0.5],
[0.2,0.2,0.5]])
l1 = criterion(Y_pred1,Y)
l2 = criterion(Y_pred2,Y)
print("Batch Loss1=",l1.data,"\nBatch Loss2",l2.data)
手写数字识别分类案例代码:
引入的包和库:


将图像转换为pytorch的tensor
将图像归一化为0-1分布

将transforms运用到dataset中:

构建模型:


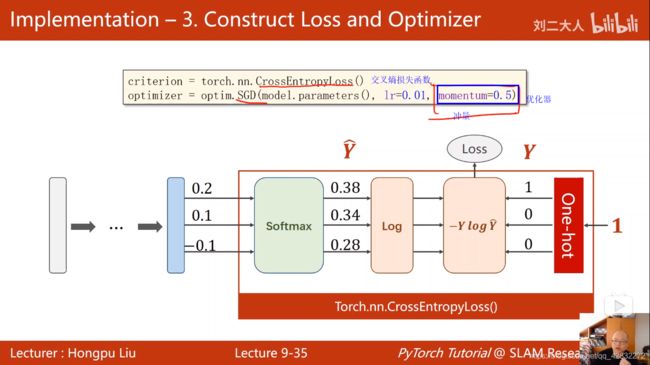
定义损失函数和优化器:
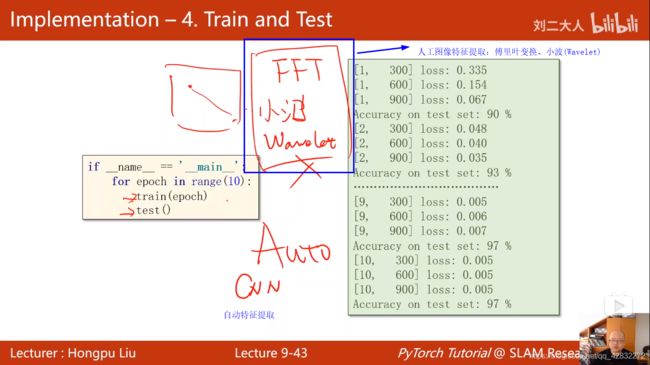
训练:


import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F #导入relu函数
import torch.optim as optim #优化器
batch_size = 64
#Normalize 归一化 0.1307 均值 0.3081 标准差
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.1307),(0.3081,))])
train_dataset = datasets.MNIST(root='../dataset/mnist/',
train=True,
download=True,
transform=transform)
train_loader = DataLoader(train_dataset,
shuffle=True,
batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/',
train = False,
download=True,
transform=transform)
test_loader = DataLoader(test_dataset,
shuffle=False,
batch_size=batch_size)
class Net(torch.nn.Module):
def __init__(self):
super(Net,self).__init__()
#线性变换,缩小维度,减少计算量
self.l1 = torch.nn.Linear(784,512)
self.l2 = torch.nn.Linear(512,256)
self.l3 = torch.nn.Linear(256,128)
self.l4 = torch.nn.Linear(128,64)
self.l5 = torch.nn.Linear(64,10) #最后变换为10个分类
def forward(self,x):
#-1 自动计算N的值 784 将图像转换为1维的长向量
x = x.view(-1,784)
#激活函数relu
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) #最后一层不做激活
model = Net()
#交叉熵损失函数
criterion = torch.nn.CrossEntropyLoss()
#momentum 冲量
optimizer = optim.SGD(model.parameters(),lr=0.01,momentum=0.5)
def train(epoch):
running_loss = 0.0
for batch_idx,data in enumerate(train_loader,0):
inputs,target = data
optimizer.zero_grad() #梯度值清零
outputs = model(inputs) #前向传播
loss = criterion(outputs,target)
loss.backward() #反向传播
optimizer.step() #更新权重
running_loss+=loss.item()
if batch_idx %300==299:
print('[%d,%5d] loss:%.3f' %(epoch+1,batch_idx+1,running_loss/300))
running_loss=0.0
def test():
correct = 0
total = 0
with torch.no_grad(): #使得以下代码执行过程中不用求梯度
for data in test_loader:
images,labels = data
outputs = model(images)
# 在每一行中求最大值的下标,返回两个参数,第一个为最大值,第二个为坐标
#dim=1 数值方向的维度为0,水平方向的维度为1
_,predicted = torch.max(outputs.data,dim=1)
total+=labels.size(0)
#当预测值与标签相同时取出并求和
correct+=(predicted==labels).sum().item()
print('Accuracy on test set:%d %%' % (100*correct/total))
if __name__=='__main__':
for epoch in range(10):
train(epoch)
test()
卷积神经网络CNN(基础篇)
卷积神经网络结构:

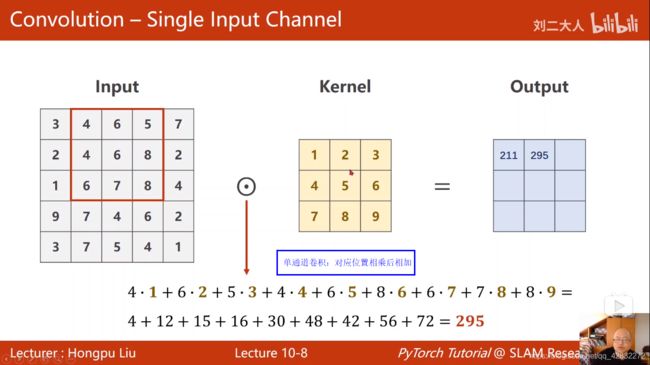
彩色图像做卷积:
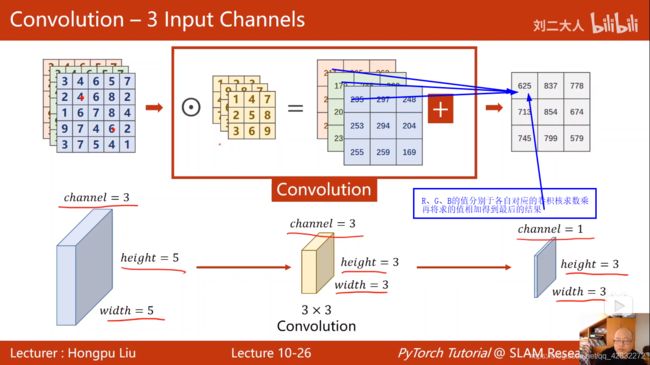
卷积核的张量有四个维度:
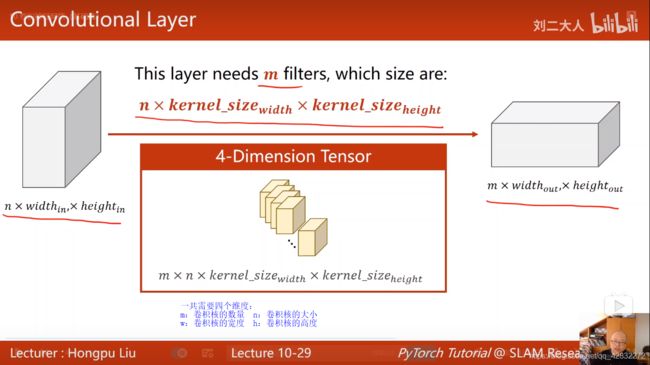

实例:

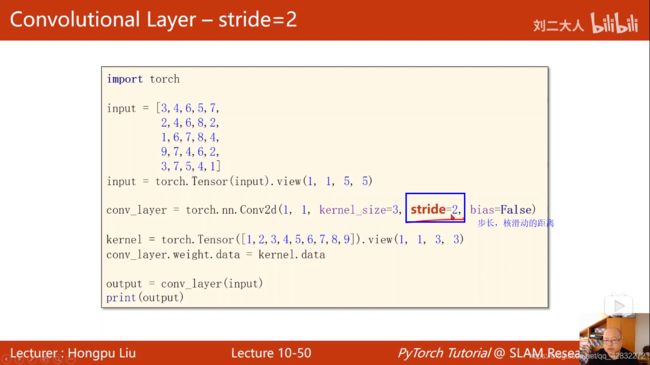
最大池化:


基本过程:
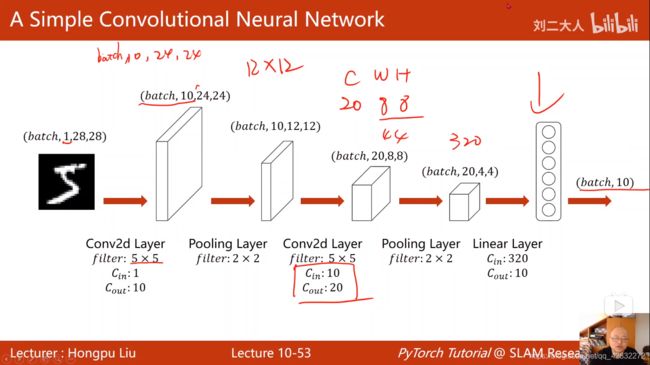

实现代码:

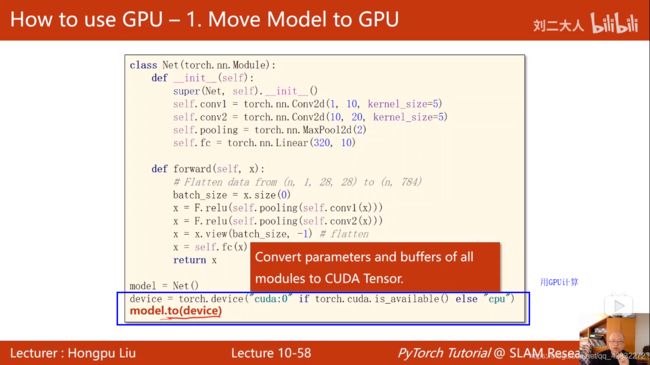

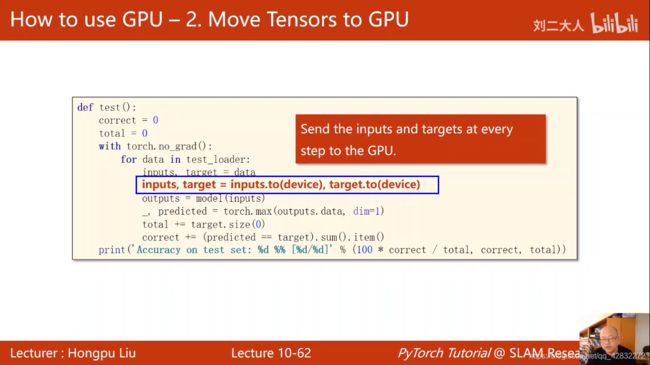
结果达到98%

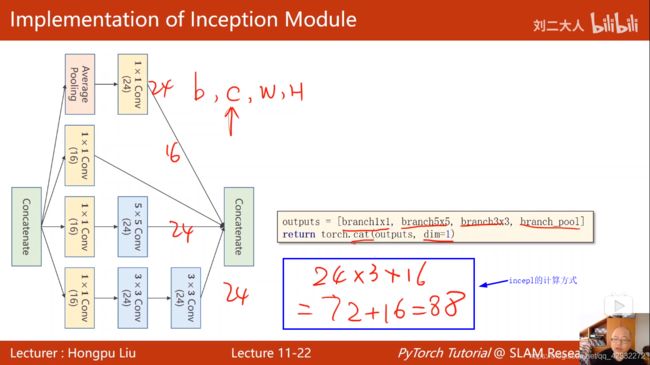
卷积神经网络CNN(高级篇)
1*1的卷积核的作用:
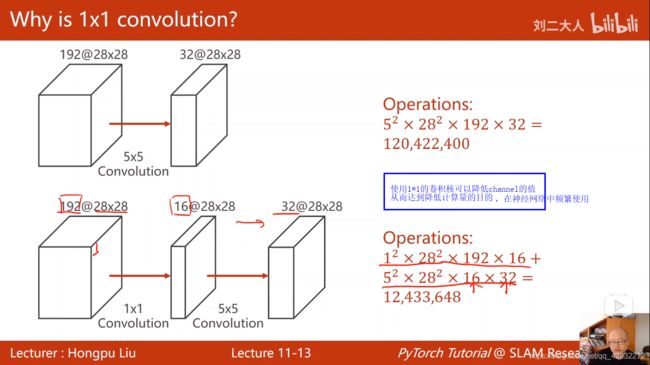


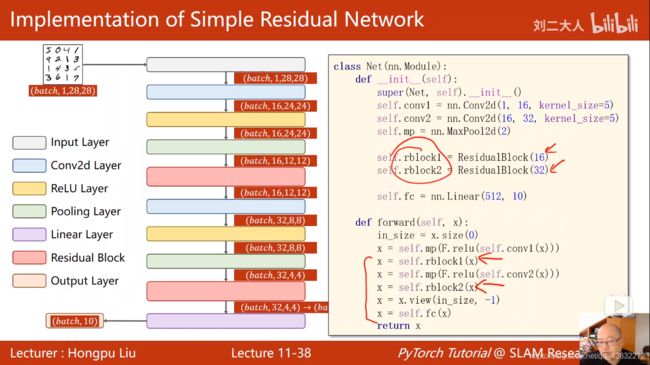
梯度消失:指在反向传播过程中,梯度始终小于1,在累乘的过程中,会逐渐趋于0,由于w=w-ag g(梯度)等于0时,w就不再改变。利用残差网络可以有效的抑制梯度消失的出现。利用残差网络要保证输出层和输入层的维度保持一致。
残差网络的实现: