排序——冒泡、选择、插入、希尔、快速、计数
目录
- 创建随机数列
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 快速排序
- 计数排序
- 归并排序
- 结果
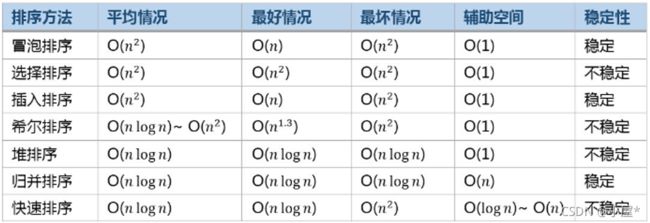
- 常见排序算法比较
创建随机数列
import random
import timeit
#创建随机的数列,n为数列个数,数列元素在0-1000之间
def randomList(n):
iList=[]
for i in range(n):
iList.append(random.randrange(1000))
return iList冒泡排序
原理:比较相邻两个数的大小,将两个数中大的交换到后一位,不断交换下去即可将最大的数放到最后一位,依次类推进行排序。
最优时间复杂度:O(n) (表示遍历一次发现没有任何可以交换的元素,排序结束。)
最坏时间复杂度:O(n2)
稳定性:稳定

#冒泡排序
def bubbleSort(iList):
if len(iList)<=1:
return iList
for i in range(1,len(iList)):
for j in range(0,len(iList)-i):
if iList[j]>=iList[j+1]:
iList[j],iList[j+1]=iList[j+1],iList[j]
return iList选择排序
原理:从数列中将最大(或最小)的数放到合适的位置,然后抛开这个数继续找下一个最大的数继续放到合适的位置。与冒泡相比,他比较的不是相邻两个数,而是该数与其他所有数的比较。但是在python中,有min(list[:])函数,所以比较适合用该方法,python下时间复杂度为O(n)
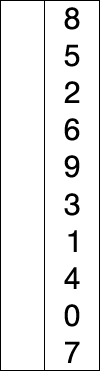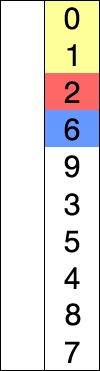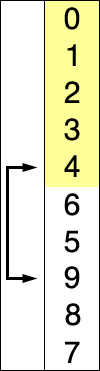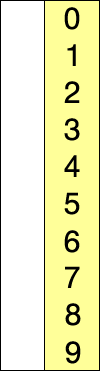
红色表示当前最小值,黄色表示已排序序列,蓝色表示当前位置。
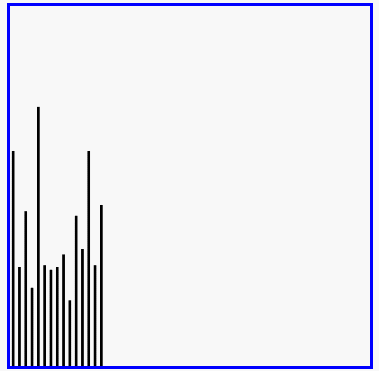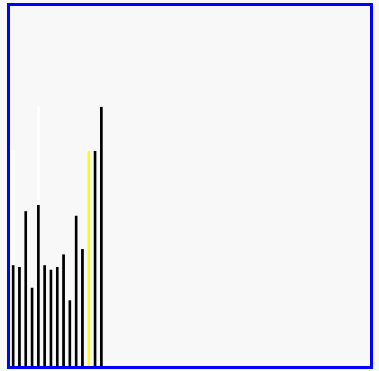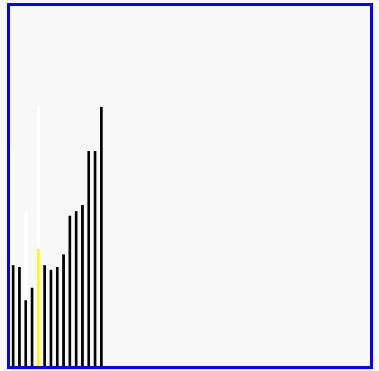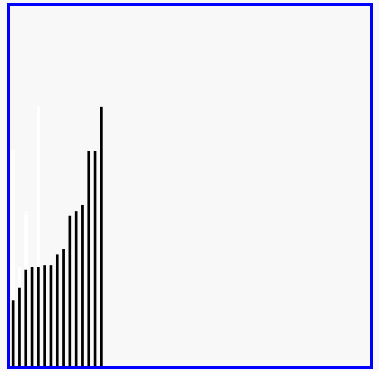
def selectSort(iList):
if len(iList)<=1:
return iList
for i in range(0,len(iList)-1):
minIdex = i
if iList[i]!=min(iList[i:]):
minIdex=iList.index(min(iList[i:]))
iList[i],iList[minIdex]=iList[minIdex],iList[i]
return iList插入排序
原理:将数列分为两部分,数列的一个数为left,其余为right。将right中的数逐一插入到left中合适的位置,直到right为空,则排序完成。时间复杂度为O(n²)
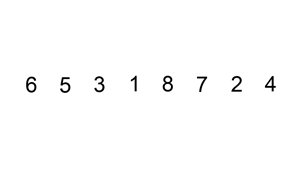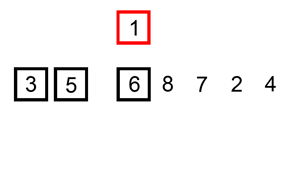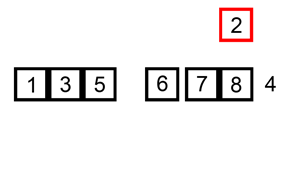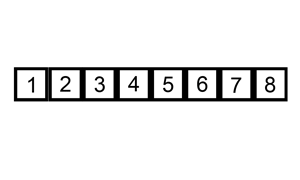

def insertionSort(iList):
if len(iList)<=1:
return iList
for right in range(1,len(iList)):
target=iList[right]
for left in range(0,right):
if target<=iList[left]:
iList[left+1:right+1]=iList[left:right]
iList[left]=target
break
return iList希尔排序
原理:又叫缩小增量排序,是种特殊的插入排序。先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。
最优时间复杂度:根据步长序列的不同而不同
最坏时间复杂度:O(n2)
稳定性:不稳定
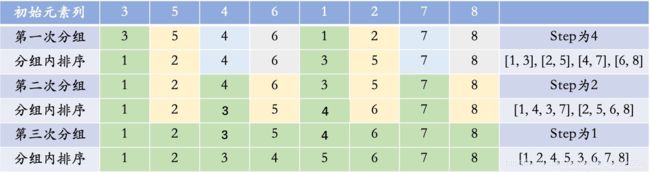
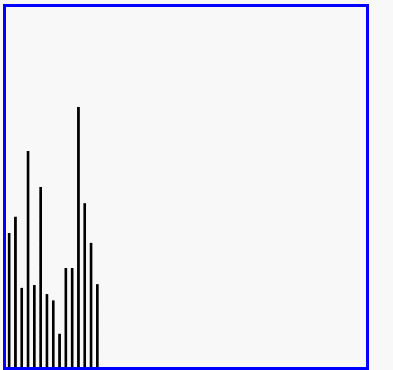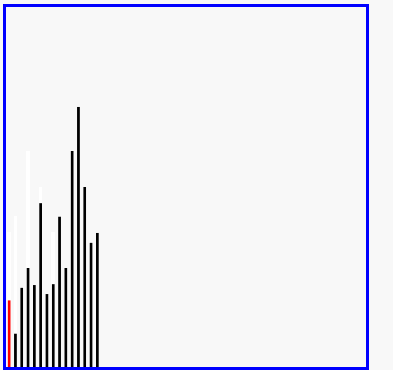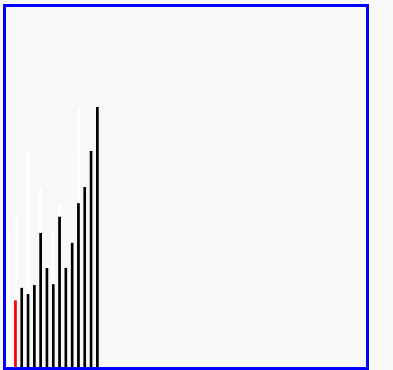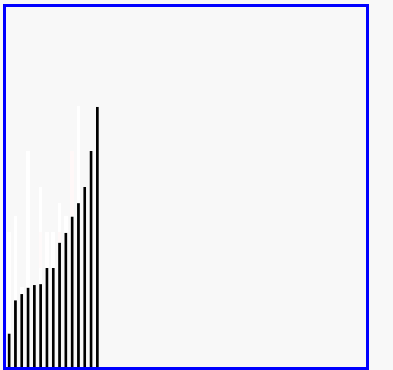
def shellSort(iList):
n = len(iList)
gap = int(n / 2)
while gap > 0:
for i in range(gap, n):
temp = iList[i]
j = i
while j >= gap and iList[j - gap] > temp:
iList[j] = iList[j - gap]
j -= gap
iList[j] = temp
gap = int(gap / 2)快速排序
原理:以数列中的某个数为基准(一般为第一个数),将列表分为左右两个子列表:左边的子列表要比基数小,右边的比基数大。然后继续分解左右两个子列表,直到无可划分。然后按照左子列表+基数+右子列表方式连接起来。
最优时间复杂度:O(nlogn)
最坏时间复杂度:O(n2)
稳定性:不稳定
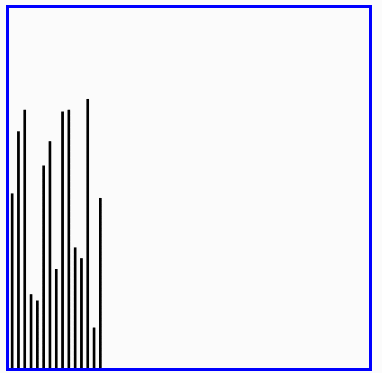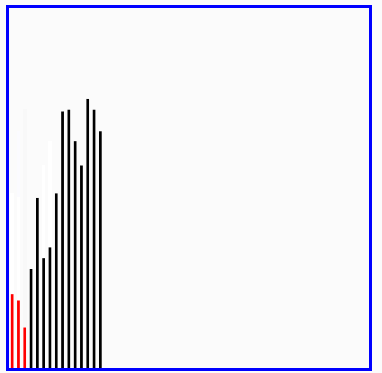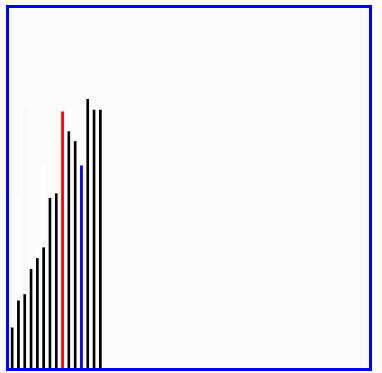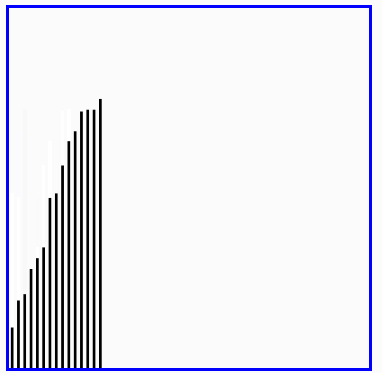
def quickSort(iList):
if len(iList)<=1:
return iList
left=[]
right=[]
for i in iList[1:]:
if i<=iList[0]:
left.append(i)
else:
right.append(i)
return quickSort(left)+[iList[0]]+quickSort(right)计数排序
原理:选择一个数为基数,然后统计数列中比其小的数的个数,如果个数为n则这个基数就放在新的数列中的第n+1的位置,也就是list[n]。相当于创建一个新的同样大小的空数列,然后按照他们的大小顺序放进去。时间复杂度O(n+k)
def countingSort(iList):
if len(iList)<=1:
return iList
ilen=len(iList)
rList=[None]*ilen
for i in range(ilen):
small=0 #用于记录比i位置小的个数
same=0 #记录相同的个数
for j in range(ilen):
if iList[j]<iList[i]:
small+=1
elif iList[j]==iList[i]:
same+=1
for k in range(small,small+same):
rList[k]=iList[i]
return rList归并排序
原理:将数组分解最小之后,然后合并两个有序数组,基本思路是比较两个数组的最前面的数,谁小就先取谁,取了后相应的指针就往后移一位。然后再比较,直至一个数组为空,最后把另一个数组的剩余部分复制过来即可。
最优时间复杂度:O(nlogn)
最坏时间复杂度:O(nlogn)
稳定性:稳定

def merge_sort(alist):
'''归并排序'''
n=len(alist)
if n<=1:
return alist
mid=n//2
#left采用归并排序后形成的有序的新列表
left_li=merge_sort(alist[:mid])
#right采用归并排序后形成的有序的新列表
right_li=merge_sort(alist[mid:])
#将两个有序子序列合并为一个新的整体
left_pointer,right_pointer=0,0
result=[]
while left_pointer<len(left_li) and right_pointer<len(right_li):
if left_li[left_pointer]<right_li[right_pointer]:
result.append(left_li[left_pointer])
left_pointer+=1
else:
result.append(right_li[right_pointer])
right_pointer+=1
result+=left_li[left_pointer:]
result+=right_li[right_pointer:]
return result
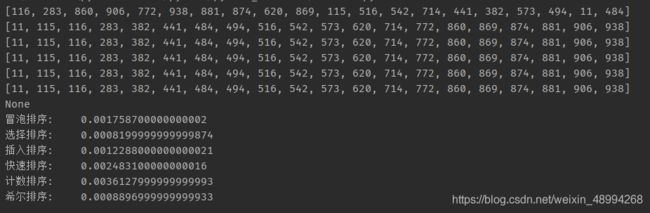
结果
if __name__=="__main__":
iList = randomList(20)
print(iList)
print(bubbleSort(iList))
print(selectSort(iList))
print(insertionSort(iList))
print(quickSort(iList))
print(countingSort(iList))
print(shellSort(iList))
print("冒泡排序:\t"+str(timeit.timeit("bubbleSort(iList)","from __main__ import bubbleSort,iList",number=100)))
print("选择排序:\t" + str(timeit.timeit("selectSort(iList)", "from __main__ import selectSort,iList", number=100)))
print("插入排序:\t" + str(timeit.timeit("insertionSort(iList)", "from __main__ import insertionSort,iList", number=100)))
print("快速排序:\t" + str(timeit.timeit("quickSort(iList)", "from __main__ import quickSort,iList", number=100)))
print("计数排序:\t" + str(timeit.timeit("countingSort(iList)", "from __main__ import countingSort,iList", number=100)))
print("希尔排序:\t" + str(timeit.timeit("shellSort(iList)", "from __main__ import shellSort,iList", number=100)))