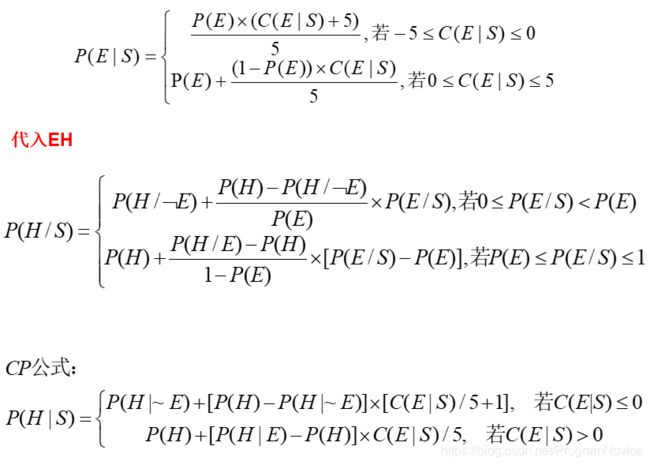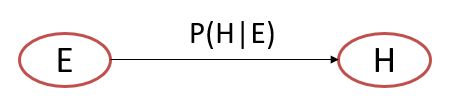《人工智能》之《非经典推理》
教材：《人工智能及其应用》，蔡自兴等，2016m清华大学出版社（第5版）
参考书：
《人工智能》之《非经典推理》
- 1 经典推理与非经典推理
- 2 不确定性推理
-
- 2.1 不确定性推理模型
- 3 概率推理
-
- 3.1 概率的基本性质和计算公式
-
- 样本空间
- 随机事件
- 频率
- 统计概率的性质
- 条件概率
- 全概率公式
- 贝叶斯公式
- 3.2 概率推理方法
- 4 主观贝叶斯方法
-
- 4.1 知识不确定性的表示
- 4.2 证据不确定性的表示
- 4.3 主观贝叶斯方法的推理过程
- 4.4 主观贝叶斯方法的优缺点
- 5 证据理论
-
- 5.1 证据理论的形式化描述
- 6.2 证据理论的不确定性推理模型
- 7 贝叶斯网络
-
- 7.1 概率图模型
- 7.2 贝叶斯网络的基本概念
- 7.3 贝叶斯网络的构造
- 7.4 贝叶斯网络的推理模式
-
- 因果推理
- 诊断推理
- 辩解推理
- 7.5 贝叶斯网络的总结
现实世界中的大多数问题是不确定、非完备的。对于这些问题，若采用前面所讨论的确定性推理方法显然是无法解决的。为此，人工智能需要研究不确定性的推理方法，以满足客观问题的需求。
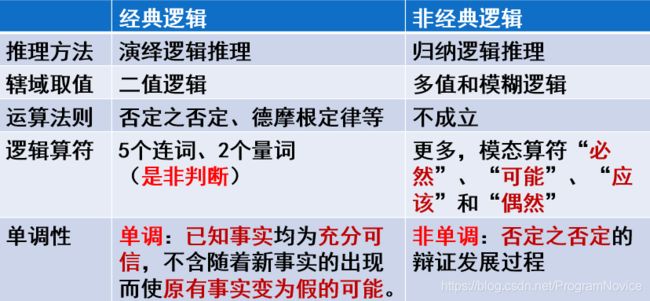
1 经典推理与非经典推理
经典推理指的是传统的命题逻辑、谓词逻辑，而非经典推理一般泛指与经典命题逻辑不同的那些逻辑。现代非经典逻辑的研究始于1910年，最早提出和创立的是美国逻辑学家刘易斯（C.I.Lewis）——建立了模态命题逻辑，波兰的J.卢卡西维茨和美国的E.L.波斯特分别于1920和1921年建立了多值逻辑。
非经典逻辑大体上分为两类：
- 与经典逻辑平行的逻辑，如多值逻辑和模糊逻辑
- 对经典逻辑进行扩充的逻辑，如模态逻辑、时态逻辑、动态逻辑
2 不确定性推理
不确定性推理，也称不精确推理，泛指除确定性推理以外的其它各种推理问题，包括不完备、不确定性知识的推理，模糊知识的推理，非单调性推理等。不确定性推理从不确定性的初始证据出发，通过运用不确定性的知识，最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。
不确定性推理存在三种不确定性，即关于知识的不确定性、关于证据的不确定性和关于结论的不确定性。
不确定性推理的基本问题
知识和证据都具有某种程度的不确定性，这就为推理机的设计与实现增加了复杂性和难度。
要解决推理方向、推理方法、控制策略等基本问题，还要解决以下问题：
- 不确定性的表示和量度
- 不确定性匹配
- 组合证据不确定性的计算
- 不确定性的传递
- 不确定性的合成
1.不确定性的表示与量度
-
知识不确定性的表示
-
证据不确定性的表示——证据的动态强度
-
不确定性的量度
2.不确定性匹配
含义：不确定的前提条件与不确定的事实匹配。
不确定性匹配算法及阈值的选择：
- 不确定性匹配算法：用来计算匹配双方相似程度的算法。
- 阈值：用来指出相似的“限度”。
3.组合证据不确定性的计算
含义: 前提条件是多个证据的组合
方法: (确定性：Certainty; 证据: Evidence; 结论: Hypothesis）
- 最大最小方法，如合取取最小、析取取最大
C(E1∧E2)=min[C(E1),C(E2)]
C(E1∨E2)=max[C(E1),C(E2)] - 概率方法，按概率公式
C(E1∧E2)=C(E1)C(E2) （Ei 彼此独立）
C(E1∨E2)=C(E1)+C(E2)-C(E1)C(E2) - 有界法
C(E1∧E2)=max[0, C(E1)+C(E2)-1]
C(E1∨E2)=min[1, C(E1)+C(E2)]
4.不确定性的传递
含义：
- 在每一步推理中，如何把证据及知识的不确定性 传递给结论。
即：C(H)=g1[C(E),f(H,E)]
表示：由规则前提E的不确定性C(E)，规则强度f(H,E)，求结论H的不确定性C(H)。（g1是一函数，该函数是根据不同的情况来定义的） - 在多步推理中，如何把初始证据的不确定性传递给最终结论
5.结论不确定性的合成
多个不同知识推出同一结论，且每条知识的前提条件是相互独立的证据，即：C(H)=g2[C1(H), C2 (H)]
表示：根据分别由独立的证据E1，E2求出的结论H的不确定性C1(H)，C2(H)，求出证据E1和E2的组合所导致的结论H的不确定性C(H)（g2是一函数，该函数是根据不同的情况来定义的）。
2.1 不确定性推理模型
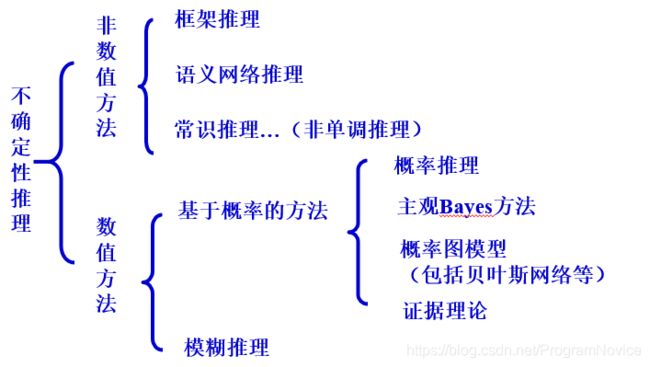
不确定性推理模型无统一的模型，种类多，比较著名的有：
- Shortliffe在1975年结合医疗专家系统MYCIN建立的可信度方法（确定性理论+概率论）
- Duda在1976年结合探矿专家系统PROSPECTOR建立的主观Bayes推理
- Dempster Shafer在1976年提出的证据理论
- Zadeh在1978年提出的可能性理论，1983年提出的模糊逻辑和逻辑推理
- Nilsson在1986年提出的概率逻辑
- Judea Pearl在1986年提出的信任网络
- Bayes提出的Bayes网络
不确定性推理的分类：
3 概率推理
3.1 概率的基本性质和计算公式
样本空间
概念：在概率论中，把试验中每一个可能出现的结果称为试验的一个样本点，由全体样本点构成的集合称为样本空间。
表示：通常，用D表示样本空间，d表示样本点。
例子：在掷币试验中，若用d1表示硬币的正面向上，用d2表示硬币的反面向上，则该试验的样本空间为：D={d1, d2}。
随机事件
概念：由样本点构成的集合称为随机事件。
例子： 在掷币试验中，若用A表示硬币正面向上这一事件，则有A={d1}
运算：
- 并事件
事件A与事件B至少有一个发生 记为A∪B - 交事件
事件A与事件B同时发生 记为A∩B - 互斥事件
事件A与B之间满足“A∩B=Φ, A∪B=D ”
频率
统计概率的性质
条件概率
全概率公式
贝叶斯公式
3.2 概率推理方法
假设有产生式规则：if E then H，证据(或前提条件) E不确定性的概率为P(E)，概率方法不确定性推理的目的就是求出在证据 E 下结论 H 发生的概率P(H|E)。
这也叫做逆概率方法。
逆概率方法的优缺点：
4 主观贝叶斯方法
1976年，杜达（R.O.Duda）、哈特（P.E.Hart）等人提出主观Bayes方法，建立了不确定性推理模型，并在地矿勘探专家系统PROSPECTOR中得到了成功的应用。
4.1 知识不确定性的表示
主观贝叶斯方法的不精确推理过程就是根据前提E的概率P(E)，利用规则的LS和LN，把结论H的先验概率P(H)更新为后验概率P(H|E)的过程。
这样，就可把取值为[0,1]的P(X)放大为取值[0,+∞)的O(X)。
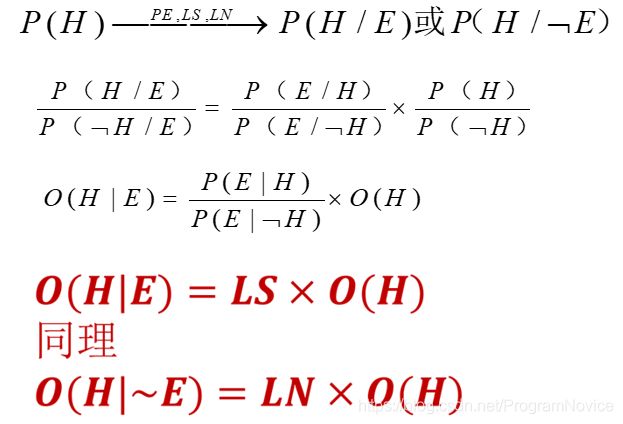
红色的两个公式就是修改的贝叶斯公式。
LS的性质
LN的性质
LS与LN的关系
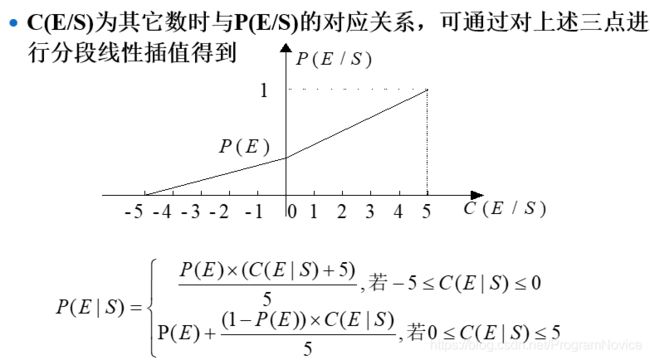
4.2 证据不确定性的表示
主观贝叶斯方法中证据的不确定性也是用概率表示的。
4.3 主观贝叶斯方法的推理过程
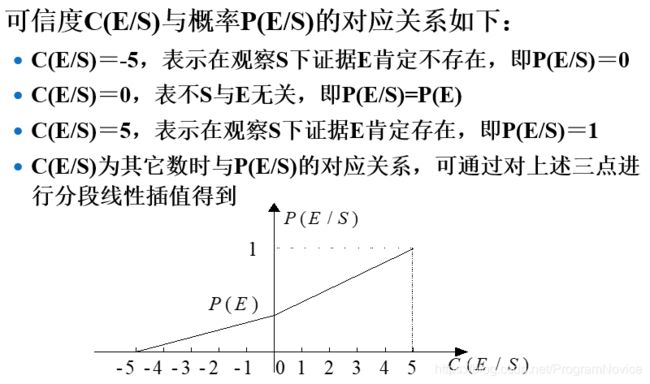
- 若采用初始证据进行推理，则通过用户得到C(E|S)，从而根据CP公式可求得 P(H|S)
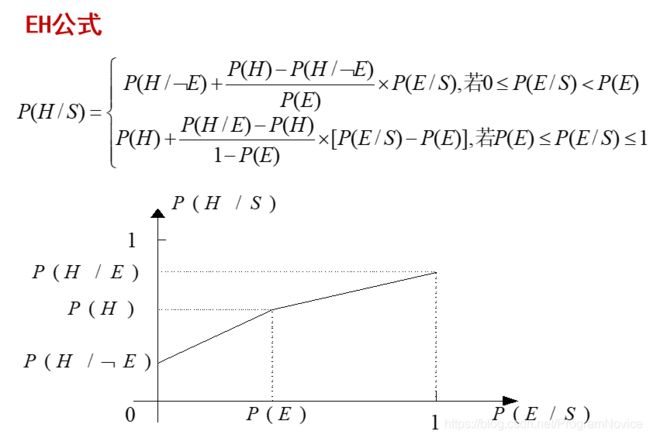
- 若采用推理过程中得到的中间结论作为证据进行推理，则通过 EH 公式可求得 P(H|S)
4.4 主观贝叶斯方法的优缺点
优点：
- 具有较坚实的理论基础。
- 知识的静态强度 LS 及LN 是由领域专家根据实践经验给出的，推出的结论有较准确的确定性。
- 主观Bayes方法是一种比较实用且较灵活的不确定性推理方法。
缺点：
- 要求领域专家在给出知识时，同时给出H的先验概率。
- Bayes定理中关于事件独立性的要求使主观Bayes方法的应用受到了限制。
5 证据理论
证据理论(theory of evidence)：又称D-S理论，是德普斯特(A.P.Dempster)首先提出，沙佛(G.Shafer) 进一步发展起来的一种处理不确定性的理论。它将概率论中的单点赋值扩展为集合赋值，比主观Bayes方法有着更大的灵活性。1981年巴纳特(J. A. Barnett)把该理论引入专家系统，同年卡威(J. Garvey)等人用它实现不确定性推理。
5.1 证据理论的形式化描述
设 D 是变量 x 所有可能取值的集合，且 D 中的元素是互斥的，在任一时刻 x 都取且只能取 D 中的某一个元素为值，则称 D 为 x 的样本空间。
在证据理论中，D 的任何一个子集 A 都对应于一个关于 x 的命题，称该命题为“ x 的值是在 A 中”。设 x ：所看到的颜色，D={红，黄，蓝}，则 A={红}表示“ x 是红色”；A={红，蓝}表示“x 或者是红色，或者是蓝色”。
1.概率分配函数
2.信任函数
3.似然函数
似然函数的另一种计算方法：
4.信任函数与似然函数的关系
5.概率分配函数的正交和
6.2 证据理论的不确定性推理模型
信任函数Bel(A)和似然函数Pl(A)分别表示命题A的信任度的下限和上限，同时也可用来表示知识强度的下限和上限。从信任函数和似然函数的定义看，它们都是建立在概率分配函数之上的，可见不同的概率分配函数将得到不同的推理模型。
下面就给出一个特殊的概率分配函数，并在其上建立推理模型。
1.概率分配函数与类概率函数
2.知识不确定性的表示
3.证据不确定性的表示
4.组合证据的不确定性的表示
5.不确定性的更新
7 贝叶斯网络
7.1 概率图模型
概率图模型是一种用图结构来描述多元随机变量之间条件独立关系的概率模型。图中的每个节点都对应一个随机变量，可以是观察变量，隐变量或是未知参数等；每个连接表示两个 随机变量之间具有依赖关系。
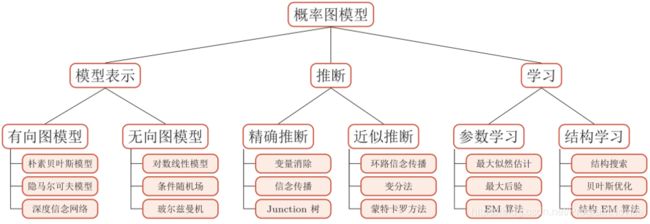
7.2 贝叶斯网络的基本概念
贝叶斯网络是表示变量间概率依赖关系的有向无环图，每个节点表示领域变量，每条边表示变量间的概率依赖关系。
贝叶斯网络用有向无环图表示：
- 结点代表证据或结论，权代表证据或结论的可信度
- 弧代表证据与结论之间的因果关系（即规则），权代表规则的可信度
局部马尔可夫性质
什么样的图是一个贝叶斯网络？
条件概率表（Condition Probability Table，CPT）
- 每个节点都对应着一个CPT，指明了该变量与父节点之间概率依赖的数量关系。
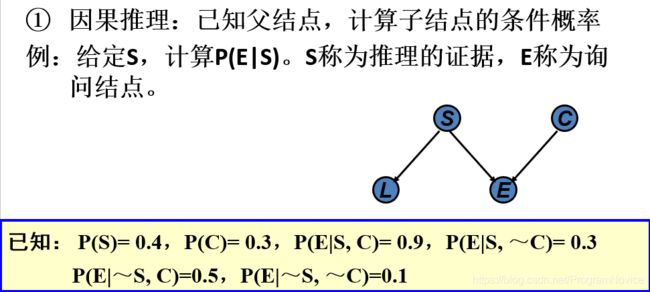
- 对所有父结点的一种指派，确定子结点的发生概率。
条件独立性
在贝叶斯网络中，如果两个节点是直接连接的，它们肯定是非条件独立的，是直接因果关系。父节点是“因”，子节点是“果”。如果两个节点不是直接连接的，但可以由一条经过其他节点的路径来连接，那么这两个节点之间的条件独立性就比较复杂。
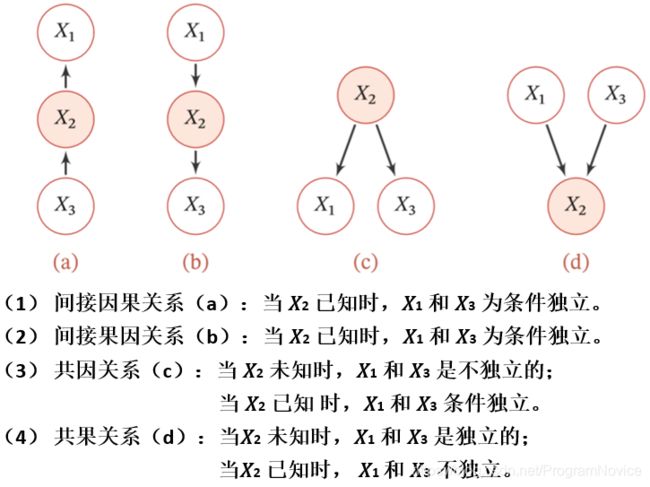
7.3 贝叶斯网络的构造
贝叶斯网络的构造方法：
- 确定变量及其解释
- 建立符合条件独立的有向无环图
- 确定局部的概率分布（CPT）
当贝叶斯网络提供了足够的条件概率，足以计算出任何联合概率，则称此贝叶斯网络是可计算的，即可推理的。
7.4 贝叶斯网络的推理模式
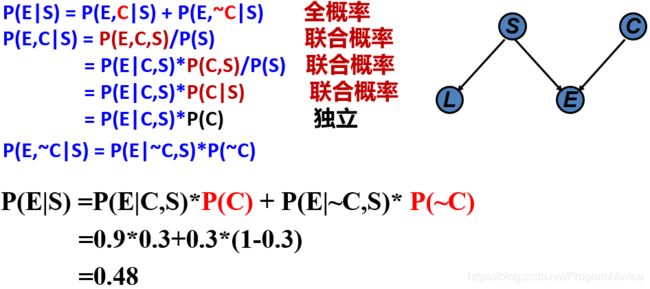
因果推理
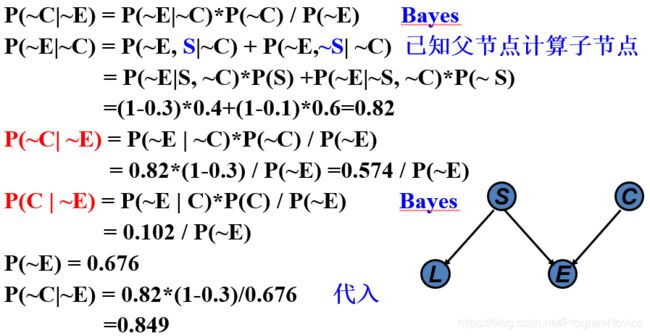
诊断推理
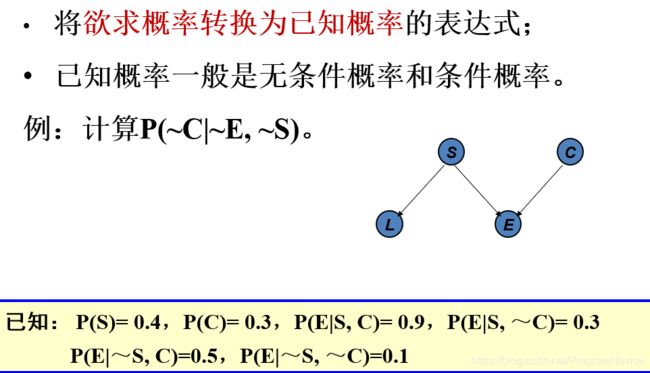
辩解推理
7.5 贝叶斯网络的总结
贝叶斯网络所依赖的一个核心概念是：条件独立（Conditional Independence）。
- 贝叶斯网络是表示不确定性知识的一种有效方法
- 贝叶斯网络的参数学习与结构学习是比较活跃的研究领域
- 贝叶斯网络的推理能够计算出任何给定事件在给定条件下发生的可能性
- 贝叶斯网络具有广阔的应用前景