线性判别分析（LDA）与Fisher判别分析（FDA）降维原理

在故障诊断中，我们常常会面对大量的且维数很高的数组，通过我们需要先对数据集进行划分及预处理，而预处理阶段极为重要的一步就是对数据进行降维特征提取，通过某种数学变换将原始高维空间转变成一个低维的子空间。

然鹅，我们常用到的基本就只有两个，一个是主成分分析（PCA），另一个则是今天所要介绍的Fisher判别分析（Fisher Discriminant Analysis，FDA）。

1. 主成分分析的基本思想：设法将原来众多具有一定相关性（比如P个指标，即主成分），重新组合成一组新的互相无关的综合指标来代替原来的指标。通过寻找在最小均方误差（Mean Square Error，MSE）下的最具代表性的投影向量，再用这些向量来表示数据。
2. Fisher判别分析的基本思想：利用已知类别的样本建立判别模型，对未知类别的样本进行分类。在最小均方误差（也就是最小二乘法MSE）意义下，寻找最能分开各个类别的最佳方向。

最先的是提出的线性判别法（Linear Discriminant Analysis，LDA），这还是一种经典的线性学习方法。在降维方面LDA是最著名的监督学习降维方法。但是，在二分类问题上，因为最早是有（Fisher，1936）提出的，因此也被称为是“Fisher判别分析（Fisher Discriminant Analysis，FDA）”。

其实LDA和FDA两种判别分析方法，是略有不同的。其中LDA则假设了各类样本数据的协方差矩阵相同，且满秩。

线性判别分析（LDA）及Fisher判别分析（FDA）

LDA的思想：由所给定的数据集，设法将样例数据投影在一条直线上，使得同类数据的投影点尽可能的接近、而异类数据的投影点之间将可能间隔更远。在我们做新样本数据的分类时，将其投影到同样的直线上，再根据投影点的位置来确定新样本的类别。如下图（源自周志华《机器学习》）所示：

这里的投影直线也用到了最小二乘的思想，所有数据样本垂直投影在直线上，只是我们的约束条件表为了不同数据样本之间的投影在直线上的距离度量。
我们需要寻找到在投影方向$w$上，使得数据样本满足两个条件：1) 相同数据之间投影距离最小；2）不同数据之间投影点位置最大（可通过求其不同数据的投影中心点来判别）

LDA二维示意图

图中，“+”和“-”代表的是两种不同的数据簇，而椭圆表示数据簇的外轮廓线，虚线表示其投影，红色实心圆●和红色实心三角形△分别代表的两类数据簇投影到$w$方向上的中心点。

对于上面投影方向$y={\mathbf{w}}^{\mathbf{T}}\mathbf{x}$，有博主认为描述的不够准确，书中并未提及关于$y$的解释，但是对于$y$其实是有所提及的。

但我认为，这里的$y$，仅仅是为了体现投影的一个方向，将数据$x$投影在方向为$w$的直线上，而不是代表的这根投影直线为 $y={\mathbf{w}}^{\mathbf{T}}\mathbf{x}$，或许会被人误认为是投影后的值0。
—菜鸡理解（如有不对，请批评指正）

已知给定的数据集为
$$D=\{(x_i,y_i){\}}_{i=1}^m，y_i\in \{0,1\}$$
假设$X_i、{\mu }_i、{\Sigma }_i$分别表示第$i\in \{0,1\}$类（注意：这里的 $i$ 指代有多少个不同的类别数据集，图中只有两类，故为0和1）示例的集合、均值向量、协方差矩阵。

假如将所有的样本数据点都投影到直线$w$上来，那么两类不同的样本数据的中心点在直线上的投影可表示为$w^T{\mu }_0、w^T{\mu }_1$；同样，所有样本投影到直线上后，我们得到的两类样本的协方差分别为$w^T{\Sigma }_{0}w$和$w^T{\Sigma }_{1}w$.

由于我们只是在一维平面上的直线，故为一维空间，由此$w^T{\mu }_0、w^T{\mu }_1、w^T{\Sigma }_{0}w、w^T{\Sigma }_{1}w$都是实数。

为什么说这里是一维空间呢？可以看上图，假设每个样本都是d维向量（上图为二维$x_1、x_2$坐标系）。现在就简单一点，想用一条直线$w$表示这些样本，称之为样本集合的一维表达。所以这里说的一维讲的是投影到一条直线上以后的数据，在直线上是属于一维空间表达的。

下面思考另一个问题，如何让同类的数据样本投影点尽可能的靠近，而使得不同样本投影点离得更远呢？

这里需要引入协方差的概念，小小复习一下协方差及样本方差的知识（因为本菜鸡数学基础差）

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。
上面的${\Sigma }_0、{\Sigma }_1$因为是自协方差也就是代表方差（也即为样本方差）。

方差：当数据分布比较分散（即数据在平均数附近波动较大）时，各个数据与平均数的差的平方和较大，方差就较大；当数据分布比较集中时，各个数据与平均数的差的平方和较小。
总的说来：方差越大，数据的波动越大；方差越小，数据的波动就越小。

---

协方差表示的是两个变量的总体的误差，这与只表示一个变量误差的方差不同。 如果两个变量的变化趋势一致，也就是说如果其中一个大于自身的期望值，另外一个也大于自身的期望值，那么两个变量之间的协方差就是正值。 如果两个变量的变化趋势相反，即其中一个大于自身的期望值，另外一个却小于自身的期望值，那么两个变量之间的协方差就是负值。
简而言之：两个变量之间差距越大，协方差就越小；相反，两个变量越相似变化趋势一致，则协方差越大。

复习完协方差、样本方差的知识后，解决上面的问题应该不难。

按照我们的需求，让同类的样本投影点尽可能的靠近，换句话说就是让同类样本投影的协方差尽可能的小（注意：这里由于是自协方差==样本方差，也就满足上面大字第一条），即$w^T{\Sigma }_{0}w+w^T{\Sigma }_{1}w$尽可能的小，这样数据的波动就小，之间的距离就更小更靠近。

关于不同数据样本投影点之间的操作，使其更加的远离。我们可以通过不同数据集投影的中心点来判别，不同中心点之间的距离越大，那么表示他们之间离得更远，则$||w^T{\mu }_0+w^T{\mu }_1|{|}_2^2$（欧式距离）更大。

好！现在我们同时考虑两者的情况，则可以使得得到最大化的目标，建立我们的模型：
$$\begin{array}{rl}J& =\frac{{\Vert {\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_0-{\mathbf{w}}^{\mathrm{T}}{\mathbf{\mu }}_1\Vert }_2^2}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_0\mathbf{w}+{\mathbf{w}}^{\mathrm{T}}{\mathbf{\Sigma }}_1\mathbf{w}}\\ & =\frac{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}\left({\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\right)\mathbf{w}}\end{array}$$
观察上式目标函数，当我们的$J\to Max$则是我们想要的结果。式子太复杂，那我们再优化一下吧。

引入一下类内和间散度矩阵的知识：

1. 类间散度矩阵用于表示各样本点围绕均值的散布情况。
2. 类内散度矩阵用于表示样本点围绕均值的散步情况，关于特征选择和提取的结果，类内散布矩阵的积越小越好。
   具体可参考这里，还有这里。

首先，我们来定义“类内散度矩阵”（within-class scatter matrix）
$$\begin{array}{rl}{\mathbf{S}}_w& ={\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1\\ & =\sum _{\mathbf{x}\in X_0}\left(\mathbf{x}-{\mathbf{\mu }}_0\right){\left(\mathbf{x}-{\mathbf{\mu }}_0\right)}^{\mathrm{T}}+\sum _{\mathbf{x}\in X_1}\left(\mathbf{x}-{\mathbf{\mu }}_1\right){\left(\mathbf{x}-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}\end{array}$$
“类间散度矩阵”（between-class scatter matrix）：
$${\mathbf{S}}_b=\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right){\left({\mathbf{\mu }}_0-{\mathbf{\mu }}_1\right)}^{\mathrm{T}}$$
然后我们的$J$可以表示为
$$J=\frac{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}}{{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}}$$
这样看起来简单多了，这就是我们的LDA想要最大化的目标函数，比较专业的说法为，$S_b$和$S_w$的“广义瑞利商”（generalizad Rayleigh quotient）。

关于“广义瑞利商”（generalizad Rayleigh quotient）的解释，可以参考这里和这里。
瑞利商经常出现在降维和聚类任务中，因为降维聚类任务往往能导出最大化最小化瑞利熵的式子，进而通过特征值分解的方式找到降维空间。
大体内容如下：

下面开始构建我们的函数及约束条件。

首先得确定我们的$w$，由于$J$的分母分子都是关于$w$的二项式子，则与$w$的长度无关，且只与方向有关。故我们令${\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1$，则：
$$\begin{array}{ll}{\min }_{\mathbf{w}}& -{\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{w}\\ \text{ s.t. }& {\mathbf{w}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{w}=1\end{array}$$
由拉格朗日乘数法（具体可参考CCA中Lagrange的应用）可得，
$${\mathbf{S}}_{\mathbf{b}}\mathbf{w}=\mathbf{\lambda }{\mathbf{S}}_{\mathbf{w}}\mathbf{w}\text{\hspace{1em}(*)}$$

其中，$\lambda$为拉格朗日乘子。

由上“类间散度矩阵”可知，${\mathbf{S}}_{\mathbf{b}}\mathbf{w}$为${\mu }_0-{\mu }_1$的平方，故${\mathbf{S}}_{\mathbf{b}}\mathbf{w}$的方向则恒为${\mu }_0-{\mu }_1$，向量的方向可以确定了，我们再令
$${\mathbf{S}}_{\mathbf{b}}\mathbf{w}=\mathbf{\lambda }({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$$

向量方向确定，$\lambda$只是代表方向向量的长度，所以${\mathbf{S}}_{\mathbf{b}}\mathbf{w}$可由上式表达。可能会有人疑惑了，这里的$\lambda$和（*）式的$\lambda$是一个$\lambda$吗？
答案是肯定的。

将上式代入(*)式，可得关于${\mathbf{S}}_{\mathbf{w}}$的式子：
$$\mathbf{w}={\mathbf{S}}_{\mathbf{w}}^{-1}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$$
这里需要对${\mathbf{S}}_{\mathbf{w}}$求逆，考虑到数值解的稳定性，常规实践操作中，需要对${\mathbf{S}}_{\mathbf{w}}$进行奇异值分解（也就是我们在矩阵理论中学到的SVD方法），原理很简单，此处，即为${\mathbf{S}}_{\mathbf{w}}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\mathbf{T}}$，其中$\Sigma$是一个实对角矩阵，对角线上的元素也就是所谓的“迹”是${\mathbf{S}}_{\mathbf{w}}$的奇异值。我们需要求解的是${\mathbf{S}}_{\mathbf{w}}$的逆，故式子变为了这样，
$${\mathbf{S}}_{\mathbf{w}}^{-1}=\mathbf{V}{\mathbf{\Sigma }}^{-1}{\mathbf{U}}^{\mathbf{T}}$$
至此，我们得到了${\mathbf{S}}_{\mathbf{w}}^{-1}$，从而可求得直线向量 $w$，找到使得 $J$ 最大的 $w$.

LDA还可从贝叶斯决策理论的角度来描述（关于贝叶斯可参考这里），可证明，当两类数据同先验、满足高斯分布（正态分布）且协方差相等时，LDA可以达到最优的分类效果。

上述讲了这么多都是二分类问题，那么关于多分类任务。

LDA推广(多分类任务)

将LDA推广到多维多分类任务，起初我们只有两类，现在我们假设有$N$类，其中第$i$类则表示为$m_i，i\in (1,N)$。

我们定义“全局散度矩阵”：
$$\begin{array}{rl}{\mathbf{S}}_t& ={\mathbf{S}}_b+{\mathbf{S}}_w\\ & =\sum _{i=1}^m\left({\mathbf{x}}_i-\mathbf{\mu }\right){\left({\mathbf{x}}_i-\mathbf{\mu }\right)}^{\mathrm{T}}\end{array}$$

其中，$\mu$代表所有示例的均值向量。

将二分类的类内散度矩阵${\mathbf{S}}_{\mathbf{w}}$重新定义为每个类别的散度矩阵之和，因为现在是对多分类任务操作，也就是将每一类的${\mathbf{S}}_{\mathbf{w}\mathbf{i}}$加起来变为一个${\mathbf{S}}_{\mathbf{w}}$，
$${\mathbf{S}}_w=\sum _{i=1}^N{\mathbf{S}}_{w_i}$$
其中，
$${\mathbf{S}}_{w_i}=\sum _{\mathbf{x}\in X_i}\left(\mathbf{x}-{\mathbf{\mu }}_i\right){\left(\mathbf{x}-{\mathbf{\mu }}_i\right)}^{\mathrm{T}}$$

同理，这里的${\mu }_i$也代表每一类的均值向量。

由上式可得到，
$$\begin{array}{rl}{\mathbf{S}}_b& ={\mathbf{S}}_t-{\mathbf{S}}_w\\ & =\sum _{i=1}^N{m}_i\left({\mathbf{\mu }}_i-\mathbf{\mu }\right){\left({\mathbf{\mu }}_i-\mathbf{\mu }\right)}^{\mathrm{T}}\end{array}$$
由此，多分类LDA可有多种实现方法，使用${\mathbf{S}}_{\mathbf{b}}、{\mathbf{S}}_{\mathbf{t}}、{\mathbf{S}}_{\mathbf{w}}$其中的任意两个即可实现目标优化。

常规采用${\mathbf{S}}_{\mathbf{b}}、{\mathbf{S}}_{\mathbf{w}}$来实现，将我们的目标进行优化，
$$\underset{\mathbf{W}}{\max }\frac{\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_b\mathbf{W}\right)}{\mathrm{tr}\left({\mathbf{W}}^{\mathrm{T}}{\mathbf{S}}_w\mathbf{W}\right)}$$

其中，$\mathbf{W}\in {\mathbb{R}}^{d\times (N-1)}$，tr(·)则表示的是矩阵的“迹”。

上式可由如下的广义特征值问题求解：
$${\mathbf{S}}_{\mathbf{b}}\mathbf{W}=\mathbf{\lambda }{\mathbf{S}}_{\mathbf{w}}\mathbf{W}$$

注意：这里的$W$和上面二分类问题时的$w$相同，$W$则是多类问题下的投影直线。故我们需要找到这样在多个类下使得满足第一部分的约束条件的直线$W$。

和二分类一样通过奇异值分解来需求解${\mathbf{S}}_{\mathbf{b}}\mathbf{w}$的值，从而得到使得优化的目标函数实现最大的 $W$，在多维中，我们可将$W$视为一个投影矩阵。

$W$的闭式解为$S_w^{-1}{S}_b$的 $d^{\prime }$个最大非零广义特征值所对应的特征向量组成的矩阵，$d^{\prime }\le N-1$.

在故障诊断中LDA也多用于对原始数据进行预处理----降维，多分类LDA将数据样本投影到$d^{\prime }$维空间中，而$d^{\prime }$往往远小于$d$维。

故可通过LDA的投影方式来降低数据的维度达到降维效果。

有一个LDA和PCA很好区分的图，附上一下：

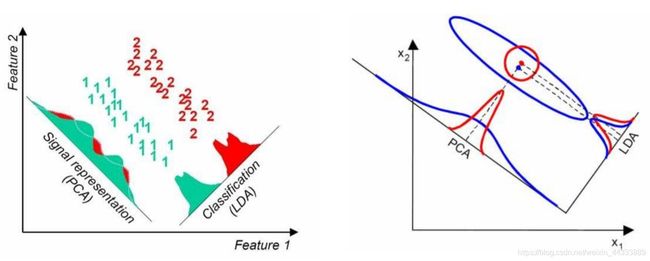
从上图中可容易理解PCA和LDA。可看出PCA多满足高斯分布，投影了最具代表性的主成分分量；而LDA如上所述，投影下来使其更容易区分出各类别之间的最佳方向。

References

1. 《机器学习》-周志华著
2. https://hyper.ai/wiki/3654
3. https://hyper.ai/wiki/9942
4. https://baike.baidu.com/item/%E6%96%B9%E5%B7%AE/3108412
5. https://baike.baidu.com/item/%E5%8D%8F%E6%96%B9%E5%B7%AE
6. https://zhuanlan.zhihu.com/p/78077834
7. https://zhuanlan.zhihu.com/p/301277905
8. https://www.zhihu.com/topic/20687704/hot
9. https://www.zhihu.com/question/27670909

❤坚持读Paper，坚持做笔记，坚持学习❤！！！
⚡To Be No.1

⚡⚡哈哈哈哈

---

⚡创作不易⚡，过路能❤关注、收藏、点个赞❤三连就最好不过了

ღ( ´･ᴗ･` )

❤

『
To the time to life, rather than to life in time to the time to life, rather than to life in time.
』