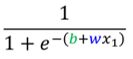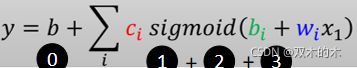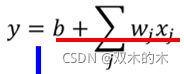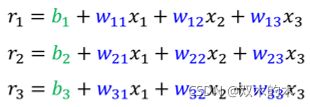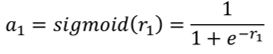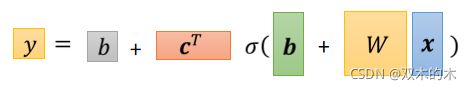1-2 李宏毅2021春季机器学习教程-第一节(下)-深度学习基本概念简介
上篇文章1-1 李宏毅2021春季机器学习教程-第一节(上)-机器学习基本概念简介介绍了回归的一些知识,重点介绍了机器学习寻找函式的三个步骤。接着我们继续学习第一节Introduction的内容。
目录
Regression
Piecewise Linear Curves
Back to ML_Step 1 :function with unknown
Back to ML_Step 2 :define loss from training data
Back to ML_Step 3: Optimization
模型变型
多做几次
好名字
Regression
Piecewise Linear Curves
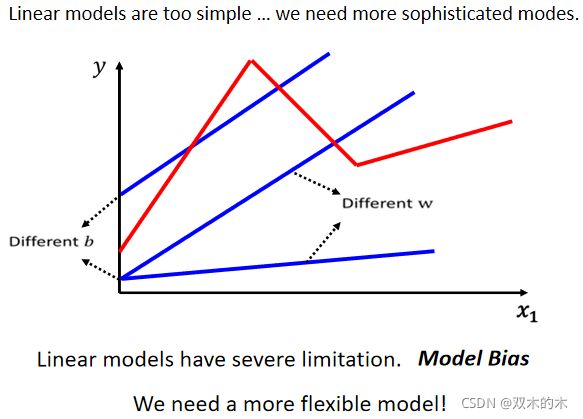
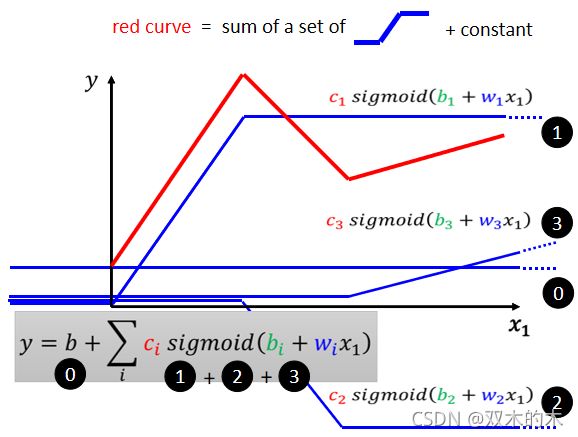
上一节讲过Linear Model,也许太过简单了,我们可以想象 x1 跟 y有比较复杂的关系,对 Linear 的 Model 来说,x1 跟 y 的关系就是一条直线,随着 x1 越来越高,y 就应该越来越大。你可以设定不同的 w,改变这条线的斜率,你可以设定不同的 b,改变这一条蓝色的直线跟 y 轴的交叉点,但是无论你怎么改 w 跟 b,它永远都是一条直线。
但也许现实并不是这个样子(如上图红线)
- 也许在 x1 小于某一个数值的时候,前一天的观看人数跟隔天的观看人数是成正比;
- 也许当 x1 大于一个数值的时候,这个物极必反,前天观看的人数太高,那隔天观看人数就会变少,也说不定;
- 也许 x1 跟 y 中间,有一个比较复杂的,像这个红色线一样的关系;
但你永远无法用 Linear 的 Model,制造红色这一条线,显然 Linear 的 Model 有很大的限制,这一种来自于 Model 的限制,叫做 Model 的 Bias。跟上一节课的 b 叫做 Bias不太一样。Model 的 Bias的意思是说,模型没有办法模拟真实的状况,所以我们需要写一个更复杂的,更有弹性的,有未知参数的 Function。
下面是精彩部分,李宏毅老师从图像的角度细分Function,引出曲线、sigmiod函数等,很绝!有种醍醐灌顶的感觉!!接着往下看吧!!!
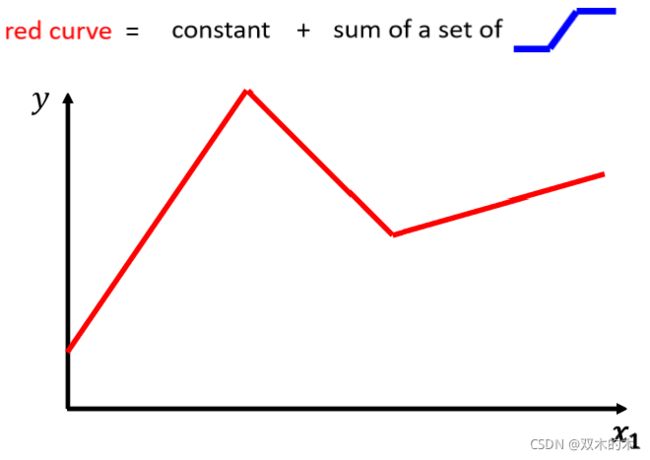
如上图,仔细观察红色的这一条曲线,它可以看作是一个常数,再加上一群蓝色的这样子的 Function。
这个蓝色 Function的特性是:
- 当输入的值小于某一个这个 Flash Hold 的时候,它是某一个定值;
- 大于另外一个 Flash Hold 的时候,又是另外一个定值;
- 中间有一个斜坡。
所以它是先水平的,然后再斜坡,然后再水平的。这边我们就先叫它蓝方吧 。 那怎么加上这个蓝色的 Function 以后,变成红色的这一条线?
①蓝线“1”Function 斜坡的起点,设在红色 Function 的起始的地方,②然后第二个,斜坡的终点设在第一个转角处,你刻意让这边这个蓝色 Function 的斜坡,跟这个红色 Function 的斜坡,它们的斜率是一样的,这个时候如果你把 0 加上 1,你就可以得到红色曲线。
③然后接下来,再加第二个蓝色的 Function,你就看红色这个线,第二个转折点出现在哪里,所以第二个蓝色 Function,它的斜坡就在红色 Function 的第一个转折点,到第二个转折点之间,你刻意让这边的斜率跟这边的斜率一样,这个时候你把 0加 1+2,你就可以得到两个转折点这边的线段,就可以得到红色的这一条线这边的部分;④然后接下来第三个部分,第二个转折点之后的部分,你就加第三个蓝色的Function,第三个蓝色的 Function,它这个坡度的起始点,故意设的跟这个转折点一样,这边的斜率,故意设的跟这边的斜率一样,接下来你把 0+1+2+3 全部加起来,你就得到红色的这个线。所以红色这个线,可以看作是一个常数,再加上一堆蓝色的 Function。
你现在这个Curves是有很多线段组成的,它是有很多锯齿状的线段所组成的,这个叫做 Piecewise Linear 的 Curves(上图红色图形)。那如果你今天 Piecewise Linear 的 Curves 越复杂,转折的点越多,那你需要的这个蓝色的 Function 就越多。
讲到这边有人可能会说,那也许我们今天要考虑的 x 跟 y 的关系不是 Piecewise Linear 的 Curves ,也许它是这样子的曲线。该怎么拟合呢?我们可以在这样的曲线上面,先取一些点,再把这些点连接起来,变成一个 Piecewise Linear 的 Curves,而这个 Piecewise Linear 的 Curves 跟原来的曲线非常接近,如果你今天点取的够多或取的位置适当的话,这个 Piecewise Linear 的 Curves,就可以逼近这一个连续的这一个曲线。
所以我们今天知道一件事情,你可以用 Piecewise Linear 的 Curves,去逼近任何的连续的曲线,而每一个 Piecewise Linear 的 Curves,又都可以用一大堆蓝色的 Function 组合起来,因此,我只要有足够的蓝色 Function 把它加起来,我也许就可以变成任何连续的曲线。
今天,假设我们的 x 跟 y 的关系非常复杂,也没关系,我们想办法写一个带有未知数的Function,这个带有未知数的 Function 表示的就是一堆蓝色的 Function,加上一个 Constant。那我们接下来的问题就是,蓝色 Function的式子应该要怎么把它写出来呢?
Back to ML_Step 1 :function with unknown
也许你要直接写出它没有那么容易,但是你可以用一条曲线来理解它,用一个Sigmoid 的 Function来逼近这个蓝色的Function,Sigmoid Function表达式为:
解释:输入的 x1,我们先乘上一个 w,再加上一个b,再取一个负号,再取 Exponential,再加 1,这一串被放在分母的地方。当然,前面可以乘上一个 Constant 叫做 c。
- 如果你今天输入的这个 x1 的值,趋近于无穷大的时候,那 e^{-(b+wx_1)}这一项就会消失,那当 x1 非常大的时候,这一条这边就会收敛在这个高度是 c 的地方。
- 那如果今天 x1 负的非常大的时候,分母的地方就会非常大,那 y 的值就会趋近于 0。
如上图所示,我们再回到这个蓝色的 Function,比较常见的名字就叫做Hard Sigmoid。我们要组出各种不同的曲线,就需要各式各样合适的蓝色的 Function,而这个合适的蓝色的 Function 怎么制造出来呢?
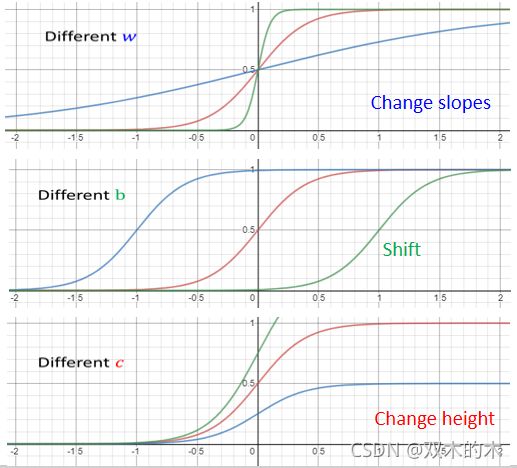
如上图所示,修改不同的参数会得到不同的效果:
- 如果你改 w ,会改变斜率(斜坡的坡度)
- 如果你改 b ,Sigmoid Function 可以左右移动
- 如果你改 c ,可以改变它的高度(曲线和y轴的交点)
因此,你只要有不同的 w 、b 和 c,你就可以制造出不同的Sigmoid Function,把不同的 Sigmoid Function 叠起来以后,你就可以去逼近各种不同的Piecewise Linear 的 Function,然后 Piecewise Linear 的 Function可以近似各种不同的 Continuous 的 Function。
如上图的红色的这条线,它的函数写出来的话,那可能长什么样子呢?
我们知道说红色这条线就是 0+1+2+3,它们都是蓝色的 Function,函式有一个固定的样子(b+wx_1),去做 Sigmoid 再乘上 c1。只是 1 跟 2 跟 3的 w 不一样,它们的 b 不一样,它们的c 不一样。如果是第一个蓝色 Function,它就是 w1、b1、c1,第二个蓝色 Function是 w2、b2、 c2,第三个蓝色 Function是 w3、b3、c3。加起来以后,我们得到的函式为 :
这个 Function里面的 b 跟 w 跟 c是未知的,都是我们未知的参数。
回忆一下,Linear Model是y = b+w x1,它有非常大的限制,这个限制叫做 Model 的 Bias,那我们要如何减少 Model 的 Bias呢?
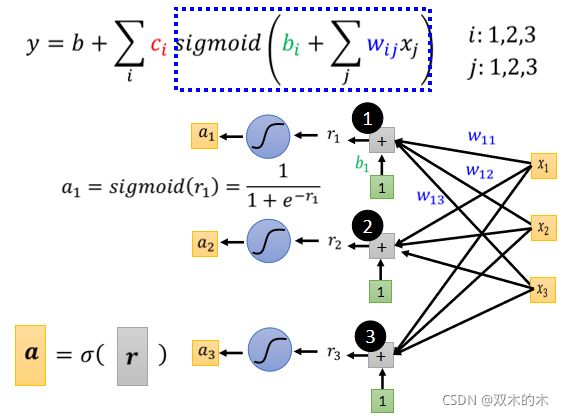
我们可以写一个更有弹性的,有未知参数的 Function,然后我们有很多不同的 bi,有很多不同的 wi,它们都通过Sigmoid 都乘上 ci,把它统统加起来再加 b 等于 y。我们只要带入不同的 c 不同的 b和不同的 w,我们就可以变出各式各样,就可以组合出各式各样不同的Function。
如果讲到这边觉得有点抽象的话,下面用直观的方式把这个式子实际上做的事情画出来。
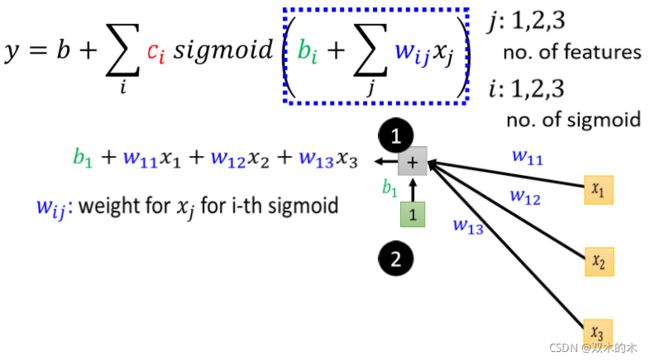
如上图,我们不是只用一个 Feature X_1,我们可以用多个 Feature。这边用j来代表 Feature 的编号。
举例来说,之前预测youtube的观看次数,如果要考虑前 28 天的话,j = 1, ... , 28;考虑前 56 天的话,j = 1, ... , 56;那如果把这个 Function再扩展成我们刚才讲的比较有弹性的 Function 的话,那也很简单,我们就把 Sigmoid 里面的东西换掉,本来这边是
那这边呢,就把这一项放到这个括号里面,改成
把本来放在这边的东西放到 Sigmoid 里面,然后呢这个每一个 Sigmoid 的 Function 里面呢,都有不同的 bi 不同的 w_ij,然后取 Sigmoid 以后乘上 ci 就全部加起来,再加上 b 就得到 y,我们只要这边 ci 、bi 跟 w_ij 在放不同的值,就可以变成不同的Function。
那如果讲到这边你还是觉得有点抽象的话,如果你看这个式子觉得有点头痛的话,那我们用比较直观的方式,把这个式子实际上做的事把它画出来,我们先考虑一下 j 就是 1 2 3 的状况,就是我们只考虑三个 Feature。
现在我们只考虑前一天前两天和前三天的 Case,所以 j 等于 1 2 3,那所以输入就是:
- x1 :前一天的观看人数,x2:两天前观看人数,x3:三天前的观看人数
- 每一个i 就代表了一个蓝色的 Function,只是我们现在每一个蓝色的 Function,都用一个 Sigmoid Function 来比近似它
那我们先来看一下,这个括号里面(下图的蓝色方框)做的事情是什么?
每一个 Sigmoid 都有一个括号,①第一个 Sigmoid 1 的Case ,就是把
- x1 乘上一个 Weight叫 w_11
- x2 乘上另外一个Weight 叫 w_12
- x3 再乘上一个Weight 叫做 w_13
- 全部把它加起来,不要忘了再加一个 b
说明:我们用 w_ij ,来代表在第 i 个 Sigmoid 里面乘给第j 个 Feature 的 Weight。对于Sigmoid1,第一个 Feature 它就是 w11,第二个Feature就是乘 w12,第三个 Feature 都是乘 w13,所以三个 Features1 2 3,这个 w 的第二个下标就是 123,w 的第一个下标代表是现我们有三个 Sigmoid Function。
同理,②第二个 Sigmoid Function,它在括号里面做的事情就是把 x1 乘上 w21,把 x2 乘上 w22,把 x3 乘上 w23,统统加起来再加 b2
③第三个 Sigmoid 呢,第三个 Sigmoid 在括号里面做的事情,就是把 x1 x2 x3,分别乘上 w31 w32 跟 w33 再加上b3。
我们现在为了简化起见,把括号里面的数字,用一个比较简单的符号r来表示。分别简记为: r1, r2,r3。
这个 x1 x2 跟 x3 和 r1 r2 r3中间的关系是什么呢?如果你熟悉线性代数的话,你可以用矩阵跟向量相乘的方法,写一个简洁的写法。它们中间的关系就是这样,把 x1 x2 x3 乘上不同的 Weight,加上不同的 Bias,也就是不同的 b 会得到不同的 r。
如上图公式,把 x1 x2 x3 拼在一起变成一个向量,把这边所有的 w 统统放在一起变成一个矩阵,把 b1 b2 b3 拼起来变成一个向量,把 r1 r2 r3 拼起来变成一个向量。
如上图最后一行,最后简写成,向量 x 乘以矩阵W(9 个数值就是9 个 权重Weight),再加上 b 就得到 r 这个向量。那这边做的事情跟上边做的事情是一模一样的,只是表示的方式不一样。
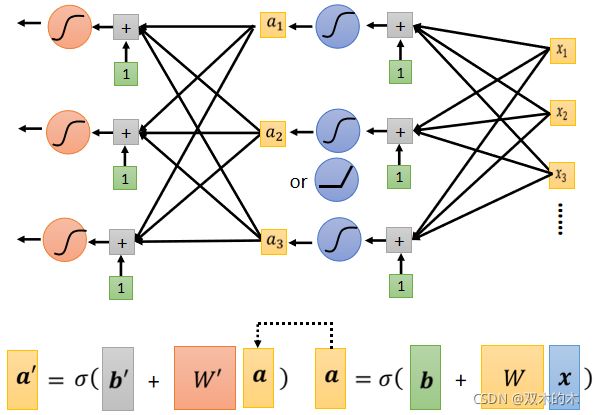
上面描述的是括号里的运算,把 x 乘上 W 加上 b 等于 r。那接下来 r 要分别通过 Sigmoid Function得到a。以r1为例:
然后同样的方法由 r2 去得到 a2,把 r3 透过 Sigmoid Function 得到 a3。
因此,上图蓝色的虚线框完成了x到a。首先通过虚线框中的括号运算从 x1 x2 x3 得到了 r1 r2 r3。接下来通过Sigmoid Function,然后得到 a1 a2 a3。
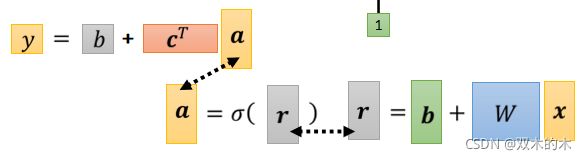
接下来我们这个Sigmoid 的输出a,还要乘上 ci 然后还要再加上 b。用向量来表示的话,a1 a2 a3 拼起来叫这个向量 a,c1 c2 c3 拼起来叫一个向量 c( 这里c 作 Transpose),那 a 乘上 c 的 Transpose 再加上 b,就得到了 y。
如上面公式,总结一下,它整体而言做的事情是输入Feature x 这个向量,x 乘上矩阵 w 加上向量 b 得到向量 r,向量 r 通过 Sigmoid Function得到向量 a,再把向量 a 跟乘上 c 的 Transpose 加上 b 就得到 y。
如果你要线性代数来表示它的话,就是下面这个式子:
继续讲怎么把这些未知的参数找出来之前,我们先再稍微重新定义一下我们的符号。
如上图所示,x 是Feature,这边的 W、b、c 跟 b(这两个 b 是不一样的,绿色是向量,灰色是数值,显示它们是不一样的东西)是我们的 Unknow Parameters(未知的参数)。
那我们把这些未知参数通通拉直,拼成一个很长的向量。我们把w 的每一个 Row,或者是每一个 Column 拿出来,今天不管你是拿过 Row 或拿 Column 都可以,你就把 w 的每一个 Column 或每一个Row 拿出来,拼成一个长的向量,把 b 拼上来,把 c 拼上来,这个长的向量,我们直接用一个符号叫做 θ来表示它。θ是一个很长的向量,里面的第一个数值我们叫 θ1,第二个叫 θ2......,它统称我们所有的未知的参数。
Q&A
- 我试着回答看看,我猜他的问题是说,我们其实要做 Optimization 这件事,找一个可以让 Loss 最小的参数,有一个最暴力的方法,就是爆收所有可能的未知参数的值,像我们刚才在只有 w 跟 b 两个参数的前提之下,我根本就可以爆收所有可能的 w 跟 b 的值嘛,所以在很少的情况下,甚至你有可能不用 Gradient Descent,不需要什么 Optimization 的技巧,但是我们今天参数很快就会变得非常多,像在这个例子里面参数有一大把,有 w b 有 c 跟 b 串起来,变成一个很长的向量叫θ,那这个时候你就不能够用爆收的方法了,你需要 Gradient Descent 这样的方法,来找出可以让 Loss 最低的参数。
- 这位同学的问题是说,刚才的例子里面有三个 Sigmoid,那为什么是三个呢,能不能够四个、 五个、六个呢,可以。Sigmoid 的数目是你自己决定的,而且 Sigmoid 的数目越多,可以产生出来的Piecewise Linear 的 Function 就越复杂。假设你只有三个 Sigmoid,意味着你只能产生三个线段,你有越多 Sigmoid,你就可以产生有越多段线的Piecewise Linear 的 Function,就可以逼近越复杂的 Function。但是至于要几个 Sigmoid,这个又是另外一个 Hyper Parameter,这个你要自己决定。我们在刚才例子里面举三个,那只是一个例子。
- Hard 的 Sigmoid,首先它的 Function 你写出来可能会比较复杂,你一下子写不出它的Function,但如果你可以写得出它的 Function 的话,你其实也可以用 Hard Sigmoid,你想要用也可以,所以不是一定只能够用刚才那个Sigmoid 去逼近那个 Hard Sigmoid,完全有别的做法,等一下我们就会讲别的做法。
Back to ML_Step 2 :define loss from training data
那接下来进入第二步:从训练数据定义loss函数。有了新的这个 Model 以后,我们 Loss 没有什么不同,定义的方法是一样的。只是我们的符号改了一下,之前是 L ( w , b ),因为 w 跟 b 是未知的,那我们现在接下来的未知的参数很多了,我们直接用 θ 来统设所有的参数,所以我们现在的 Loss Function 就变成 L( θ )。
如上图所示,这个 Loss Function 要问的就是,这个 θ 如果它是某一组数值的话,会有多不好或有多好,那计算的方法,跟只有两个参数的时候,其实是一模一样的。
- 先给定某一组 W、b、c^T跟 b的初始值
- 然后把一种 Feature x 带进去,然后看看你估测出来的 y 是多少
- 再计算一下跟真实的 Label 之间的差距,你得到一个 e
- 把所有的误差通通加起来,你就得到你的 Loss
Back to ML_Step 3: Optimization
接下来下一步就是优化(Optimization),Optimization跟前面讲的没有什么不同,就算我们换了一个新的模型,下面是这个 Optimization 的步骤。
现在的 θ 它是一个很长的向量,要找一组 θ让我们的 Loss 越小越好,可以让 Loss 最小的那一组 θ,我们叫做 θ Star,θ^*,具体步骤如下:
- (1)我们一开始要随机选一个初始的数值θ_0。你可以随机选,之后也会讲到更好的找初始值的方法,我们现在先随机选就好。
- (2)接下来要计算微分,你要对每一个未知的参数,这边用θ1 θ2 θ3 来表示,都去计算它对 L 的微分,那把每一个参数都拿去计算对 L 的微分以后,集合起来它就是一个向量,那个向量我们用 g 来表示它。这边假设有 1000 个参数,这个向量的长度就是 1000,这个向量里面就有 1000 个数字,这个向量名字叫做Gradient。Gradient 的表示方法是 L 前面放了一个倒三角形,这是一个简写的方法,意思就是把所有的参数 θ1 θ2 θ3,通通拿去对 L 作微分。那后面放 θ0 的意思是说,我们这个算微分的位置,是在 θ 等于 θ_0 的地方,我们算出这个 Gradient。
- (3)算出这个 g 以后,接下来呢我们Update参数。更新的方法跟刚才只有两个参数的状况是一模一样的,只是从更新两个参数,可能换成更新成 1000 个参数,但更新的方法是一样的。本来有一个参数叫 θ1,上标 0代表它是一个起始的值,它是一个随机选的起始的值,把这个θ_1^0减掉η 乘上微分的值,得到 θ_1^1,代表 θ1 更新过一次的结果,θ_2^0 减掉微分乘以,减掉 η 乘上微分的值,得到θ_2^1,以此类推,你就可以把那 1000 个参数统统都更新了。
把这边所有的 θ 合起来当做一个向量,用 θ^0 来表示,把 η 提出来,那剩下每一个参数对 L 微分的部分,叫做 Gradient 叫做 g,所以 θ^0 减掉 η 乘上 g,就得到 θ^1 ← θ^0-ηg 。
如上面公式,θ0 减掉 η 乘上 g(一个向量)会得到 θ1。那假设你这边参数有 1000 个,那 θ0 就是 1000个数值,1000 维向量,g 是1000 维的向量,θ1 也是 1000维的向量。那整个操作就是①由 θ0 算 Gradient,根据 Gradient 去把 θ0 更新成 θ1,②然后呢再算一次Gradient,然后根据 Gradient 把 θ1 再更新成 θ2,③再算一次 Gradient 把θ2 更新成 θ3,以此类推直到你不想做或者是你算出来的这个Gradient是 0 向量(Zero Vector),导致你没有办法再更新参数为止,不过在实作上你几乎不太可能,通常你会停下来就是你不想做了。
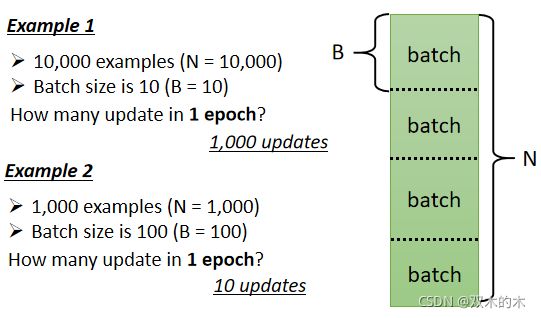
再提一个概念Batch。如上图,但是实际上我们在做 Gradient的时会这么做:我们这边有大 N 笔资料,我们会把这大 N 笔资料分成一个一个的 Batch(一包一包的东西,一组一组的),随机分就好,所以每个 Batch 里面有大B 笔资料,所以本来全部有大 N 笔资料,现在大B笔资料一组,一组叫做 Batch。
那本来我们是把所有的 Data 拿出来算一个 Loss,那现在我们只拿一个 Batch 里面的 Data出来算一个 Loss,我们这边把它叫 L1,那跟这个 L 以示区别,因为你把全部的资料拿出来算 Loss,跟只拿一个 Batch 拿出来的资料拿出来算 Loss,它不会一样嘛,所以这边用 L1 来表示它。
假设这个 B 够大,也许 L 跟 L1 会很接近,所以实作上(如上图),每次我们会先选一个 Batch,用这个 Batch 来算L,根据这个 L1 来算 Gradient,用这个 Gradient 来更新参数,接下来再选下一个 Batch 算出 L2,根据 L2 算出Gradient,然后再更新参数,再取下一个 Batch 算出L3,根据 L3 算出 Gradient,再用 L3 算出来的 Gradient 来更新参数。所以我们并不是拿大 L 来算Gradient,实际上我们是拿一个 Batch 算出来的L1 L2 L3,来计算 Gradient,那把所有的 Batch 都看过一次,叫做一个 Epoch,每一次更新参数叫做一次 Update, Update 跟 Epoch 是不一样的东西(每次更新一次参数叫做一次 Update,把所有的 Batch 都看过一遍,叫做一个 Epoch)。
那至于为什么要分一个一个 Batch,那这个我们下周再讲,但是为了让大家更清楚认识,Update 跟 Epoch 的差别,这边就举一个例子。
(1)第一个例子,假设我们有 10000 笔 Data,也就是N = 10000,假设我们的 Batch 的大小是设 10,也就B = 10。 接下来问,我们在一个 Epoch 中,总共 Update 了几次参数?
10000 笔 Example总共形成了 10000 除以 10,也就是 1000个 Batch,所以在一个 Epoch 里面,你其实已经更新了参数 1000 次,所以一个 Epoch 并不是更新参数一次,在这个例子里面一个 Epoch,已经更新了参数 1000 次。
(2)第二个例子,假设有 1000 个资料,Batch Size=100,那其实 Batch Size 的大小也是你自己决定的(也是一个 HyperParameter),1000 个 Example,Batch Size 设 100,那1个 Epoch 总共更新几次参数呢,是1000/100 = 10 次。
所以做了一个 Epoch 的训练,你其实不知道它更新了几次参数,有可能 1000 次,也有可能 10 次,取决于它的 Batch Size 有多大。
补充:所谓 HyperParameter 就是你自己决定的东西,人所设的东西不是机器自己找出来的,叫做 HyperParameter,我们今天已经听到了,几个 Sigmoid 也是一个 HyperParameters,Batch Size 也是一个 HyperParameter。
模型变型
那我们其实还可以对模型做更多的变形.这个 Hard Sigmoid 不好吗,为什么我们一定要把它换成 Soft 的Sigmoid?
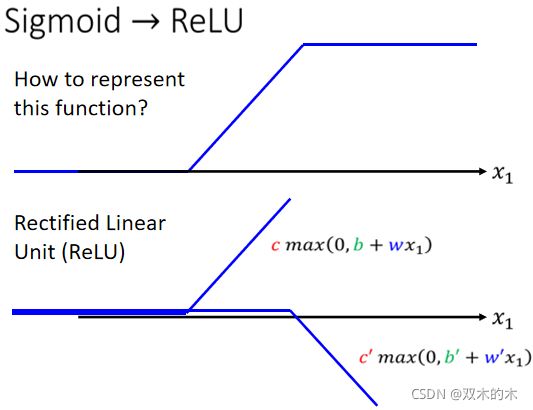
你确实可以不一定要换成 Soft 的 Sigmoid,有其他的做法。举例来说这个 Hard 的 Sigmoid,我刚才说它的函式有点难写出来,其实也没有那么难写出来,它可以看作是两个 Rectified Linear Unit 的加总,所谓 Rectified Linear Unit (ReLU)它就是长这个样。
如上图,它有一个水平的线,走到某个地方有一个转折的点,然后变成一个斜坡,那这种Function 它的式子,写成 c* max(0, b+ wx_1) ,这个max(0, b + wx_1)的意思就是比较大的那个当做输出。
那总之这一条线,可以写成c* max(0, b + wx_1),每条不同的 w 不同的 b 不同的 c,你就可以挪动它的位置,你就可以改变这条线的斜率,在机器学习里面,这条线我们叫做 Rectified Linear Unit,它的缩写叫做ReLU。
把两个 ReLU 叠起来就可以变成 Hard 的 Sigmoid。
那本来这边只有 i 个Sigmoid,你要 2 个ReLU,才能够合成一个 Hard Sigmoid ,所以这边有 i 个 Sigmoid,那如果ReLU 要做到一样的事情,那你可能需要 2 倍的 ReLU,所以我们把 Sigmoid 换成 ReLU。这边就是把一个式子换了,因为要表示一个 Hard 的 Sigmoid,表示那个蓝色的 Function 不是只有一种做法,你完全可以用其他的做法。那这个 Sigmoid或是 ReLU,他们在机器学习里面,我们就叫Activation Function。
当然还有其他常见的 Activation Function,但 Sigmoid 跟 ReLU,应该是今天最常见的 Activation Function,那哪一种比较好呢,这个我们下次再讲,哪一种比较好呢,我接下来的实验都选择用了 ReLU,显然 ReLU 比较好,至于它为什么比较好,那就是下周的事情了。
接下来就真的做了这个实验,这个都是真实的数据。
- 如果是 Linear 的 Model,我们现在考虑 56 天,训练资料上面的 Loss 是 0.32k,没看过的资料 2021 年资料是 0.46k。
- 如果用 10 个 ReLU,好像没有进步太多(0.45k),这边跟用 Linear 是差不多的,所以看起来 10 个 ReLU 不太够。100 个 ReLU 就有显着的差别了,在训练资料上的 Loss就可以从 0.32k 降到 0.28k,我们就可以制造比较复杂的曲线,在测试资料上也好了一些(0.43k)。
- 接下来换 1000 个 ReLU,在训练资料上 Loss 更低了一些(0.27k),但是在没看过的资料上,看起来也没有太大的进步(0.43k)。
多做几次
接下来还可以做什么呢,我们还可以继续改我们的模型。
举例来说,刚才我们说从 x 到a 做的事情,是把 x 乘上 w 加 b,再通过 Sigmoid Function,不过我们现在已经知道不一定要通过 Sigmoid Function,ReLU 也可以,然后得到 a。
我们可以把这个同样的事情,再反复地多做几次。刚才我们把 x 乘上 w 加 b,通过 Sigmoid Function 得到 a,我们可以把 a 再乘上另外一个 w’,再加上另外一个 b’,再通过Sigmoid Function,或 RuLU Function,得到 a’,所以我们可以把 x,做这一连串的运算产生 a,接下来把 a 做这一连串的运算产生a’,那我们可以反复地多做几次,要做几次,这个又是另外一个 Hyper Parameter,你要做两次吗?三次吗?四次吗?一百次吗?这个你自己决定,不过这边的 w 跟这边的 w’,它们不是同一个参数喔,这个 b 跟这边的 b’,它们不是同一个参数,是增加了更多的未知的参数。
那就是接下来就真的做实验,我们就是每次都加 100 个 ReLU,那我们就是 Input Features,就是 56 天前的资料。
- 如果是只做一次,就x乘上 w 再加 b,再通过ReLU 或 Sigmoid,这件事只做一次的话,这是我们刚才看到的结果。两次的话,这个 Loss 降低很多,0.28k 降到 0.18k,没看过的资料上也好了一些三层,又有进步,从 0.18k 降到 0.14k,所以一层就是乘一次 w,到通过一次 ReLU,到通过三次 ReLU,我们可以从 0.28k 到 0.14k,在训练资料上,在没看过的资料上,从 0.43k 降到了 0.38k,看起来也是有一点进步的。
那这个是那个真实的实验结果啦,就我们来看一下,今天有做通过三次 ReLU 的时候,做出来的结果怎么样。
- 横轴就是时间
- 纵轴是观看的人次(千人)
- 红色的线代表的是真实的数据
- 蓝色的线是预测出来的数据
那你会发现说,在这种低点的地方啊,你看红色的数据是每隔一段时间,就会有两天的低点,在低点的地方,机器的预测还算是蛮准确的。那这边有一个神奇的事情,这个机器高估了真实的观看人次,尤其是在这一天(上图红色圆圈),这一天有一个很明显的低谷,但是机器没有预测到这一天有明显的低谷,它是晚一天才预测出低谷。
这天最低点就是除夕啊,谁除夕还学机器学习。所以当然对机器来说,你不能怪它,它根本不知道除夕是什么,它只知道看前 56 天的值,来预测下一天会发生什么事,所以它不知道那一天是除夕,所以你不能怪它预测地不准,这一天就是除夕。
好名字
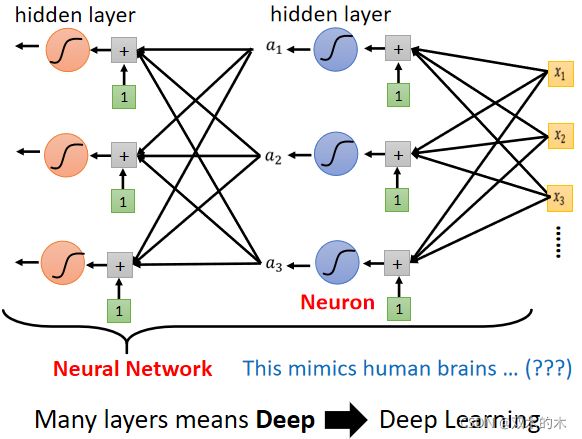
到目前为止,我们讲了很多各式各样的模型,那我们现在还缺了一个东西,缺一个好名字。这些 Sigmoid 或 ReLU叫做 Neuron,很多的 Neuron 就叫做 Neural Network。Neuron 就是神经元,人脑中就是有很多神经元,很多神经元串起来就是一个神经网路,跟你的脑是一样的,接下来你就可以说,这个模型就是在模拟人们脑,这个就是人工智能。
但是在 80 90 年代的时候,Neural Network 不是什么新的技术,当时已经把这个技术的名字搞到臭掉了,因为之前吹捧得太过浮夸,所以后来大家对 Neural Network 这个名字都非常地感冒,写在 Paper 上面都注定害你的 Paper 被拒绝, 所以后来为了要重振 Neural Network 的雄风,需要新的名字。这边有很多的 Neural,每一排 Neural 我们就叫它一个 Layer,它们叫 Hidden Layer,有很多的 Hidden Layer 就叫做 Deep,这整套技术就叫做 Deep Learning。
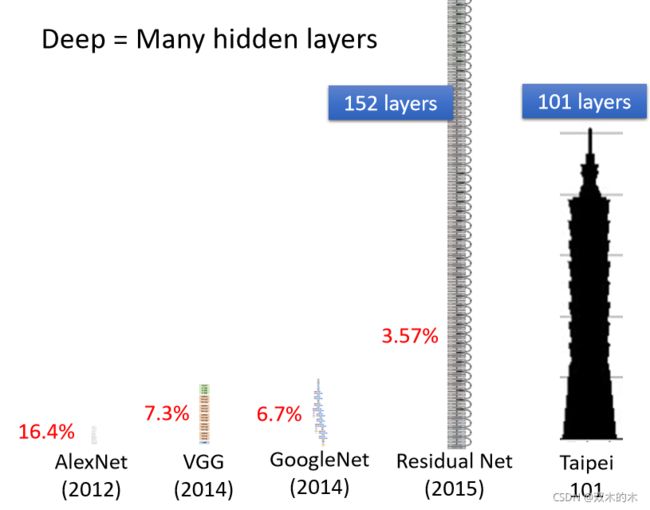
Deep就是这样来的,所以人们就开始,把类神经网路越叠越多、越叠越深,12 年的时候有一个 AlexNet,它有 8 层,它的错误率是 16.4%,两年之后 VGG 19层,错误率在影像辨识上进步到 7.3 %,这个都是在影像辨识上一个,这个基准的资料库上面的结果,后来GoogleNet 有错误率降到 6.7%,有 22 层,但这些都不算是什么。
Residual Net 有 152 层啊,它比 101 还要高啊,但是这个 Residual Net 啊,其实要训练这么深的 Network 是有诀窍的,这个我们之后再讲。
如果你仔细思考一下,我们一路的讲法的话,你有没有发现一个奇妙的违和的地方,我们一开始说,我们想要用 ReLU 或者是 Sigmoid,去逼近一个复杂的 Function,实际上只要够多的 ReLU 够多的 Sigmoid,就可以逼近任何的连续的 Function ,我们只要有够多的 Sigmoid,就可以知道够复杂的线段,就可以逼近任何的 Continuous 的 Function,所以我们只要一排 ReLU 一排 Sigmoid,够多就足够了,那深的意义到底何在呢?
把 ReLU Sigmoid Function 反复用,到底有什么好处呢,为什么不把它们直接排一排呢,直接排一排也可以表示任何 Function 。ReLU Sigmoid 排成一排,你只可以制造一个肥胖的 Network,Fat Neural Network,跟 Deep Neural Network 听起来,量级就不太一样,Deep 听起来就比较厉害啦,Fat Neural Network 还以为是死肥宅 Network,就不厉害这样子,那到底 Deep 的理由,为什么我们不把 Network 变胖,只把 Network 变深呢,这个是我们日后要再讲的话题。
那有人就说,那怎么不变得更深呢,刚才只做到 3 层,应该要做得更深嘛,现在 Network 都是叠几百层的啊,没几百层都不好意思说,你在叫做 Deep Learning,所以要做更深。
在实际的数据中,4 层在训练资料上,它的Loss 是 0.1k,在没有看过 2021 年的资料上,是如何呢? 是 0.44k,惨掉了。在训练资料上,3 层比 4 层差,4 层比 3 层好,但是在没看过的资料上,4 层比较差,3 层比较好,在训练资料上,跟没看过的资料上,它的结果是不一致的。这种训练资料跟测试资料,它的结果是不一致的状况叫做 Overfitting,机器学习会发生 Overfitting 的问题,指的就是在训练资料上有变好,但是在没看过的资料上没有变好这件事情。
但是做到目前为止,我们都还没有真的发挥这个模型的力量。
所以我们要真正做的事情是预测未知的资料,但是如果我们要预测未知的资料,我们应该选 3 层的 Network,还是 4 层的 Network 呢。举例来说今天是 2 月 26 号,今天的观看人数我们还不知道,如果我们要用一个 Neural Network,用我们已经训练出来的 Neural Network,去预测今天的观看人数。
至于怎么选模型,这个是下周会讲的问题,但是大家都非常有 Sense,知道我们要选 3 层的,多数人都决定要选 3 层的,你可能会说我怎么不选 4 层呢,4 层在训练资料上的结果比较好啊,可是我们并不在意训练资料的结果啊,我们在意的是没有看过的资料,而 2 月 26 号是没有看过的资料,我们应该选一个在训练的时候,没有看过的资料上表现会好的模型,所以我们应该选 3 层的 Network。
那你可能以为这门课就到这边结束了,其实不是,我们真的来预测一下,2 月 26 号应该要有的观看次数是多少,但是因为其实 YouTube 的统计,它没有那么及时,所以它现在只统计到 2 月 24 号,没关系,我们先计算一下 2 月 25 号的观看人数,这个 3 层的 Network 告诉我说,2月 25 号这个频道的总观看人次,应该是 5250 人,那我们先假设 2 月 25 号是对的,但实际上我还不知道 2 月 25 号对不对,因为YouTube 后台统计的数据还没有出来啊,但我们先假设这一天都是对的,然后再给我们的模型去预测 2 月 26 号的数字,得到的结果是 3.96k 有 3960 次,那它为什么这边特别低,因为模型知道说,这个礼拜五观看的人数,就是比较少啊,所以它预测特别低,听起来也是合理的。
好,那今天其实就讲了深度学习,那今天讲的不是一般的介绍方式,如果你想要听一般的介绍方式,过去的课程影片也是有的,我就把链接(上图)附在这边,然后深度学习的训练,会用到一个东西叫Backpropagation,其实它就是比较有效率,算 Gradients 的方法,跟我们今天讲的东西没有什么不同,但如果你真的很想知道,Backpropagation 是什么的话,影片链接也附在这边。
说明:记录学习笔记,如果错误欢迎指正!写文章不易,转载请联系我。