（有监督）Python实现Logistic回归算法(学习笔记)

一、前言

数据挖掘十大算法–logistic算法。广义的线性回归分析模型，常用于数据挖掘，疾病自动诊断，经济预测等领域，实际上是一种分类方法，主要用于两分问题。逻辑回归主要解决的问题是：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

logistic算法虽然简单，但是很经典，对于后续有监督学习算法的学习理解会有很大的帮助。
FLAG：以后相关的机器学习算法都要自己编程实现，然后和相关的库函数实现做一个对比。

二、实验环境

• python3.6.4
• IDE：Pycharm 2018
• 操作系统：windows10
• 吴恩达逻辑回归数据集
• 依赖库：scipy，matplotlib， numpy，pandas，sklearn

三、Logistic回归的基本原理

---

###3.1、算法简介
logistic回归算法原理：面对一个回归或者分类问题，建立代价函数，然后通过优化方法迭代求解出最优的模型参数，然后测试验证我们这个求解的模型的好坏。

logistic回归算法的关键之处在于：

• 寻找决策面函数
• 构造代价函数
• 利用数值寻优算法来迭代代价函数，从而得到优化参数值

###3.2、数学推导过程

具体的推导过程过程如下：

---

---

---

###3.3、行业应用

• 1、预测
• 2、找关键影响因素
• 3、二分类问题

---

###3.3、算法迭代步骤

• step1：数据预处理，划分训练集和测试集，并根据需求标准化或者归一化数据集（预处理）
• step2：根据特征分布来确定决策面方程形式（一般为多项式）
• step3：根据代价函数，利用相应优化算法（梯度法等）迭代出方程参数
• step4：根据决策面函数来进行预测或者是分类
• step5：计算分类的准确率（模型评估）

四、logistic回归算法的编程实现（python）

本实例用到得到实验数据为吴恩达机器学习课程上关于logitic回归的数据集（数据集为1003的形式，包括1002的特征以及100*1的二分类结果），并且对数据进行分割，从而形成训练集和测试集。

我们下面的实现，主要是分为三个部分：

• 1、利用梯度下降法，纯编程实现（帮助理解算法实现过程）
• 2、利用python的scipy.optimize模块，使用共轭梯度法来迭代实现
• 3、利用python的sklearn.linear_model.LogisticRegression模块来实现（最简单实用）

---

利用梯度下降法，纯编程实现的脚本如下：

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

# 这两句代码用来正确显示图中的中文字体，后续都要加上
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

data = pd.read_csv('https://myblog-wss.oss-cn-hongkong.aliyuncs.com/logistic/ex2data1.txt',
                   names = ['exam1','exam2','adm'])
#利用pandas布尔索引的得到两类样本，并绘图
postive = data[data.adm == 1]
negetive = data[data.adm == 0]
#数据预处理，选出实际训练使用数据
data = data.values
X = data[:,:-1]
m = X.shape[0]
one = np.ones((m,1))
X = np.hstack((one,data[:,:-1]))
# print(X.shape)
Y = data[:,-1:]

def boundary(theta):
    x1 = np.arange(20,100,0.5)
    x2 = (theta[0,0]+theta[0,1]*x1)/(-theta[0,2])#直线方程为:theta[0] + theta[1]*x1 + theta[2]*x2 = 0
    plt.plot(x1, x2,c = 'r',linewidth = 2,label = '决策边界')
    plt.scatter(postive['exam1'],postive['exam2'],c = '#ff7500',label = '正样本')
    plt.scatter(negetive['exam1'],negetive['exam2'],c = '#725e82',label = '负样本')
    plt.legend()
    plt.show()


'''
使用自己编写的梯度下降(上升)法来处理，吴恩达课后作业数据集
'''

# print(np.mat(Y).shape)

def sigmoid(x):
    return 1.0/(1+np.exp(-x))
def gradascent(xtrain,ytrain,max = 50000,alpha=0.1):
    xtrain_m=np.mat(xtrain)
    ytrain_m=np.mat(ytrain)
    m,n = np.shape(xtrain_m)
    weights = np.ones((n,1))
    for k in range(max):
        h = sigmoid(xtrain_m*weights)
        error = -(ytrain_m-h)
        weights = weights - alpha*xtrain_m.transpose()*error
    return weights

def prediction(theta,x):
    h = sigmoid(np.mat(x)*theta)
    return np.where(h>=0.5,1,0)
def accuracy(pre,y):
    accu = np.mean(pre == y)
    # accu = np.mean([1 if a == b else 0 for (a,b) in zip(pre_y,y)])
    return accu

theta = gradascent(X,Y,max = 500000,alpha=0.001)

print(theta.ravel())
pre_y = prediction(theta,X)
accur = accuracy(pre_y,Y)
print('(梯度下降法迭代自编脚本)logistic分类识别率: ' + repr(accur) + '%')
boundary(theta.ravel())

• 脚本输出结果

(machine_learning) D:\CloudMusic\virtualenv\machine_learning\machine>python logistic_sklearn.py
[[-547.63901451    4.73006368    4.61109921]]
(梯度下降法迭代自编脚本)logistic分类识别率: 92.0%

• 脚本分类可视化（仅仅针对二维特征可实现）

---

上面的代码是自己编程实现的logistic回归算法，下面我们再来直接调用最优化库相关的代码来实现参数优化：

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import scipy.optimize as opt #引入最优化模块
# import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn import datasets

# 这两句代码用来正确显示图中的中文字体，后续都要加上
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
#
data = pd.read_csv('https://myblog-wss.oss-cn-hongkong.aliyuncs.com/logistic/ex2data1.txt',
                   names = ['exam1','exam2','adm'])
#利用pandas布尔索引的得到两类样本，并绘图
postive = data[data.adm == 1]
negetive = data[data.adm == 0]


data = data.values
X = data[:,:-1]
m = X.shape[0]
one = np.ones((m,1))
X = np.hstack((one,data[:,:-1]))
y = data[:,-1:].ravel()

##下面来实现logistic算法

def sigmoid(x):
    return 1./(1.+np.exp(-x))

# x = np.arange(-10,10,0.1)
# plt.plot(x,sigomoid(x),c='#725e82',linewidth = 3)
# plt.show()

#输出概率函数
def out(x,w):
    return sigmoid(np.dot(x,w))

#编写损失函数J（theta）函数,其中theta为优化参数，x是输入向量，y是输出向量
def cost(theta,X,y):
    # h = out(x,theta)
    # J = -1*np.mean(y*np.log(h)+(1-y)*np.log((1-h)))
    # return J
    return -(y.dot(np.log(sigmoid(X.dot(theta)))) + (1 - y).dot(1 - np.log(sigmoid(X.dot(theta))))) / len(y)

#编写梯度计算函数，这里有一个梯度函数向量化的推导要注意看

def grad(theta, x, y):
    # return ((sigomoid(x.dot(theta))-y).T).dot(x)
    g = x.T.dot((out(x, theta) - y)) / len(x)
    # g = grad.ravel()
    return g


#定义预测函数
def prediction(theta,x):
    h = out(x,theta)
    # return [1 if x>=0.5 else 0 for x in h]#返回一个列表
    return np.where(h>=0.5,1,0)

#定义预测准确度函数

def accuracy(pre_y,y):
    accu = np.mean(pre_y == y)
    # accu = np.mean([1 if a == b else 0 for (a,b) in zip(pre_y,y)])
    return accu

# 绘制决策边界
def boundary(theta):
    x1 = np.arange(20,100,0.5)
    x2 = (theta[0]+theta[1]*x1)/(-theta[2])#直线方程为:theta[0] + theta[1]*x1 + theta[2]*x2 = 0
    plt.plot(x1, x2,c = 'r',linewidth = 2,label = '决策边界')
    plt.scatter(postive['exam1'],postive['exam2'],c = '#ff7500',label = '正样本')
    plt.scatter(negetive['exam1'],negetive['exam2'],c = '#725e82',label = '负样本')
    plt.legend()
    plt.show()
# 测试函数编写是否正确
initial_theta = np.zeros(X.shape[1])


##使用最优化模块来学习theta参数，优化算法可选。有个大坑，算法选择为'TNC'牛顿截断法
# scipy’s fmin_tnc doesn’t work well with column or row vector. It expects the parameters to be in an array format.
res = opt.minimize(fun=cost,x0=initial_theta.flatten(),args=(X,y.flatten()),method='tnc',jac=grad)
# result = opt.fmin_tnc(func=cost, x0=theta.flatten(), fprime=grad, args=(X, y.flatten()))
'''
两者的功能是一致的，将多维数组降为一维，但是两者的区别是返回拷贝还是返回视图，np.flatten(0返回一份拷贝，对拷贝所做修改不会影响原始矩阵，
而np.ravel()返回的是视图，修改时会影响原始矩阵
'''
# print(theta.flatten().shape)#二维数组降为一维，因为opt.minimize()的一些参数不支持多维数组，比如向量形式
# print(res_theta.ravel().shape)
# print(res)#打印参数优化结果
res_theta = res.x[:,np.newaxis]#一维数组转化为二维数组
print(res_theta)
# print(cost(res_theta, X, y))
pre = prediction(res_theta,X)
# print(len(pre))
print('使用最优化模块opt.minimize来学习theta参数识别成功率: ' + repr(accuracy(pre.ravel(),y)*100) + '%')

boundary(res_theta)

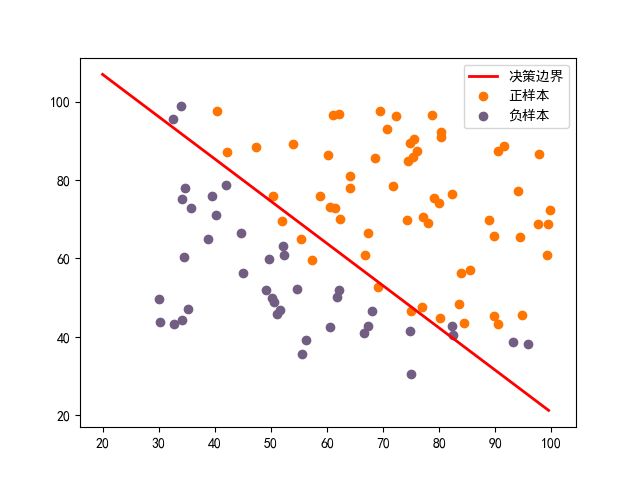
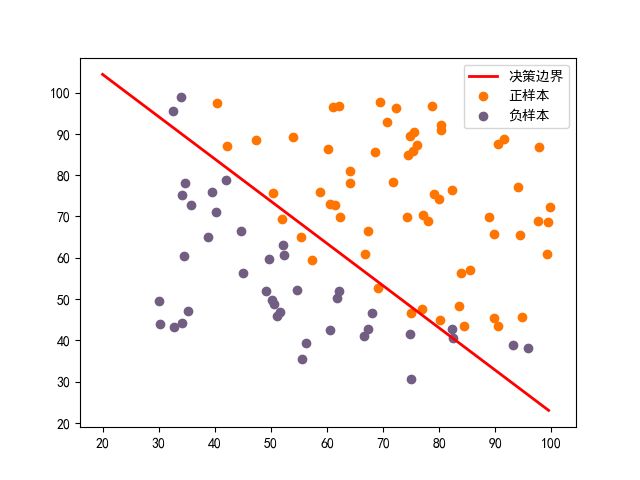
• 可视化决策面分类效果图

---

• 实验输出结果（决策面参数以及识别测试成功率）

(machine_learning) D:\CloudMusic\virtualenv\machine_learning\machine>python logistic_regression.py
[[-23.68500523]
 [  0.19862744]
 [  0.18435949]]
使用最优化模块opt.minimize来学习theta参数识别成功率: 89.0%

五、logistic回归算法的scikit-learn库实现

实现的脚本如下：

#!/usr/bin/env python 
# -*- coding:utf-8 -*-
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression


# 这两句代码用来正确显示图中的中文字体，后续都要加上
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

'''
首先研究sklearn包对于吴恩达课后习题的的二分类测试集
class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, tol=0.0001, C=1.0, 
fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’liblinear’, 
max_iter=100, multi_class=’ovr’, verbose=0, warm_start=False, n_jobs=1)
'''
data = pd.read_csv('https://myblog-wss.oss-cn-hongkong.aliyuncs.com/logistic/ex2data1.txt',
                   names = ['exam1','exam2','adm'])
#利用pandas布尔索引的得到两类样本，并绘图
postive = data[data.adm == 1]
negetive = data[data.adm == 0]
#数据预处理，选出实际训练使用数据
data = data.values
X = data[:,:-1]
m = X.shape[0]
one = np.ones((m,1))
# X = np.hstack((one,data[:,:-1]))
# print(X.shape)
Y = data[:,-1:]

x_train,x_test,y_train,y_test =train_test_split(X, Y, test_size=0.1)
log = LogisticRegression(penalty = 'l2',tol= 1e-8 ,solver ='lbfgs')#给定一个逻辑回归分类器
log.fit(X,Y.ravel())#根据给定的训练数据拟合模型。
score = log.score(x_test,y_test)#测试集与标签的预测准确率
theta = [log.intercept_[0],log.coef_.ravel()[0],log.coef_.ravel()[1]]#获取优化参数结果
print(theta)#打印优化参数
print('机器学习库sklearn.linear_model识别成功率: ' + repr(score*100) + '%')
print(log.n_iter_)#打印迭代次数
def boundary(theta):
    x1 = np.arange(20,100,0.5)
    x2 = (theta[0]+theta[1]*x1)/(-theta[2])#直线方程为:theta[0] + theta[1]*x1 + theta[2]*x2 = 0
    plt.plot(x1, x2,c = 'r',linewidth = 2,label = '决策边界')
    plt.scatter(postive['exam1'],postive['exam2'],c = '#ff7500',label = '正样本')
    plt.scatter(negetive['exam1'],negetive['exam2'],c = '#725e82',label = '负样本')
    plt.legend()
    plt.show()

boundary(theta)

---

• 使用scikit-learnj机器学习库实现逻辑回归分类的预测实际对比图

• 实验对比(自编脚本和scikit-learnj机器学习库实现的对比)

(machine_learning) D:\CloudMusic\virtualenv\machine_learning\machine>python logistic_sklearn.py
[-25.052193143127443, 0.2053549121857798, 0.20058380395530143]
(梯度下降法迭代自编脚本)logistic分类识别率: 92.0%
机器学习库sklearn.linear_model识别成功率: 90.0%
运行次数：32

根据上述的的实验结果可以看出，自编脚本与scikit-learnj第三方库实现的结果基本一致，存在微小的差异。自编脚本的实验准确度之所以高不是因为梯度下降法好，而是因为采用库实现自带正则化处理，防止过拟合现象的发生，因此准确的说，应该还是scikit-learnj第三方库实现的结果更加可靠。而且采用第三方库只迭代了32次就收敛，而使用梯度下降法则是迭代了50000此，方法好坏显而易见。应用上还是直接调用来的方便和准确。
但是自编也是为了更好的熟悉算法流程。

六、总结

6.1 、Logistic回归算法的主要优点：

• 1、速度快适合用于二分类问题，原理简单，算法迭代速度快，运行效率高；
• 2、容易更新模型，从而吸收新的数据，应用十分广泛，是传统有监督算法的经典。

6.2、Logistic回归算法的主要缺点：

• 1、对数据和场景的适应能力有局限性，不如决策树算法适应性那么强

适用条件与主要用途：

• 1、一般用于二分类问题较多；
• 2、寻找主要的影响因素：这一点和多元线性回归类似，不过因变量是二元变量数据；
• 3、预测：根据决策方程，从而预测某一事件发生的概率；
• 4、判别分类：常用二分类任务

###6.3、logistic回归与多元线性回归的区别

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。
这一家族中的模型形式基本上都差不多，不同的就是因变量不同。这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

• 因变量连续，就是多元线性回归问题
• 因变量为二项分布就是logistic回归
• 如果是poisson分布，就是poisson回归问题

七、参考文章链接和推荐的教程

• 机器学习算法–逻辑回归原理介绍
• 逻辑回归-理论篇
• 数据挖掘经典算法：Logistic(逻辑回归) python和sklearn实现
• 预处理数据的方法总结（使用sklearn-preprocessing）
• python之sklearn学习笔记
• sklearn.neighbors.KNeighborsRegressor 函数官方文档
• logistic回归算法-维基百科
• 机器学习算法的随机数据生成
• sklearn API
• sklearn官网