【神经网络与深度学习-TensorFlow实践】-中国大学MOOC课程（五）（NumPy科学计算库））

第5讲 NumPy科学计算库

5.1 多维数组

• Python拥有出色的第三方库生态系统
• 在机器学习中，需要把所有的输入数据，都转变为多为数组的形式。
• score[i, j]二维数组i,j都从0开始

score[5] = [85, 72, 61, 92, 80]
score[2,5] = [[85, 72, 61, 92, 80],[85, 72, 61, 92, 80]]
score[30,5] = [[85, 72, 61, 92, 80],
				...
			  [85, 72, 61, 92, 80]]

5.1.1 数组的形状（Shape）

描述数组的维度，以及各个唯独内部的元素个数。(n0,n1,...,ni,...nm)

shape:(30,5)#这是一个二维数组，形状是一个元组，使用一个小括号括起来，第一个数字30表示在第一个维度中有30个元素，第二个数字5表示在第二个维度中有5个元素，形状(30,5)表示这是一个30*5的二维矩阵

score[5] = [85, 72, 61, 92, 80]#对于这个一维数组，维度是1，形状中应该只有一个数字，数组中有5个数字，所以长度是5
shape:(5,)#形状是5，逗号','表示这是一个元组

• 数组的形状用一个元组来表示，它描述了数组的维数和长度
• 几维数组就有几个数字，每个数字对应一个维度，这个维度中有几个元素这个数字就是几，表示这个维度的长度

例子：对于一个10个班级，30个同学，10科成绩来说

score[i,j,k] = [...]
shape:(10,30,5)

5.2 创建NumPy数组

• 多维数组

1. 形状（Shape）：是一个元组，描述数组的维度，以及各个维度的长度
2. 长度（Length）：某个维度的元素个数

• Python中的数组的创建主要依赖于第三方库NumPy库，是一个专门用来处理多维数组的库

1. 提供了多维数组、矩阵的常用操作和一些高效的科学计算函数
2. 底层运算通过C语言实现，处理速度快、效率高，适用于大规模多维数组。
3. 可以直接完成数组和矩阵运算，无需循环。

5.2.1 安装NumPy库

• Anaconda：安装anaconda之后，NumPy库就已经被安装好了
• pip安装pip install numpy

5.2.2 导入NumPy库

• 方式一

常用方式

使用的时候必须加前缀

import numpy as np#会起一个别名np

• 方式二
  以这种方式使用的时候不用加前缀，但是为了同名函数的混淆，不建议这么做

from numpy import * 

5.2.3 创建数组

• NumPy要求数组中所有元素的数据类型都必须是一致的
• Python支持的数据类型仅有整型、浮点型和fushuxing（没听懂）
• 在使用Python列表或元组、创建NumPy数组时，所创建的数组类型，由原来的元素类型推导而来##### 5.2.3.1 创建一维数组

array([列表]/(元组))

例子：创建一维数组的例子

>>>a = np.array([0,1,2,3])

>>>a#直接输出数组名可以看到数组的定义
array([0, 1, 2, 3])

>>>print(a)#使用print()函数输出数组中的元素
[0,1,2,3]

>>>type(a)#使用type()函数可以得到a的类型
<class 'numpy.ndarray'>#是一个ndarry对象

>>>a[0]#使用索引访问numpy中的对象
0

>>>print(a[1],a[2],a[3])#使用print()函数输出指定的元素
1 2 3

>>>a[ 0:3 ]#和列表类似，也可以使用切片
array([0,1,2])
>>>a[ :3 ]
array([0,1,2])
>>>a[ 0: ]
array([0,1,2,3])

5.2.3.2 数组的属性

属性	描述
ndim	数组的维数
shape	数组的形状
size	数组元素的总个数
dtype	数组中元素的数据类型
itemsize	数组中每个元素的字节数

拿刚才建立的数组当例子：

>>>a = np.array([0,1,2,3])
>>>a#直接输出数组名可以看到数组的定义
array([0, 1, 2, 3])

>>>a.ndim
1
>>>a.shape
(4,)
>>>a.size
4

5.2.3.3 创建二维数组

>>>b = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])
>>>b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

>>> b[0]
array([0, 1, 2, 3])
>>> b[0][0]#和双下标有同样的效果
0
>>> b[0,1]
1

>>> b.ndim#维数
2
>>> b.shape#形状
(3, 4)
>>> b.size#大小
12

5.2.3.4 创建三维数组

>>> t = np.array([[[0,1,2,3],[4,5,6,7],[8,9,10,11]],[[12,13,14,15],[16,17,18,19],[20,21,22,23]]])
>>> t
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

#对三维数组的使用
>>> t[0]
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> t[0][0]
array([0, 1, 2, 3])
>>> t[0][0][0]
0
>>> t[0][0][0]
0

#三维数组中的信息
>>> t.ndim
3
>>> t.shape
(2, 3, 4)
>>> t.size
24

#三维数组中的二维数组的信息
>>> t[0].ndim
2
>>> t[0].shape
(3, 4)
>>> t[0].size
12

5.2.3.5 NumPy新增的数组元素的数据类型

5.2.3.6 指定数组的数据类型

• 在使用Python列表或元组、创建NumPy数组时，所创建的数组类型，由原来的元素类型推导而来

array([列表]/(元组),dtype = numpy.数据类型)

一维数组例子：

>>> a = np.array([0,1,2,3],dtype = np.int64)
>>> a
array([0, 1, 2, 3], dtype=int64)


>>> a.dtype#a的类型
dtype('int64')
>>> a.itemsize#a的每个元素中的字节数
8

二维数组浮点数例子：
直接创建浮点数数组

>>> c = np.array([1.2,3.5,5.1])
>>> c.dtype
dtype('float64')
>>> c.itemsize
8

5.2.3.7 创建特殊的数组

函数	功能描述
np.arange()	创建数字序列数组
np.ones()	创建全1数组
np.zeros()	创建全0数组
np.eye()	创建单位矩阵
np.linspace()	创建等差数列
np.logspace()	创建等比数列

• arrange()函数：创建一个由数字序列构成的数组。从起始数字开始到结束数字，生成一个连续增加的序列

1. 前闭后开：数字序列中不包括结束数字；
2. 起始数字省略时，默认从0开始；
3. 步长省略时，默认为1

np.arange(起始数字,结束数字,步长,dtyoe=数据类型)

>>> np.arange(4)
array([0, 1, 2, 3])
>>> d = np.arange(0, 2, 0.3)
>>> d
array([0. , 0.3, 0.6, 0.9, 1.2, 1.5, 1.8])

• ones()函数：创建一个元素全部为1的数组

np.ones(shape,dtype=数据类型)#数据类型可以省略


>>> np.ones((3,2),dtype=np.int16)
array([[1, 1],
       [1, 1],
       [1, 1]], dtype=int16)
>>> np.ones((3,2))
array([[1., 1.],
       [1., 1.],
       [1., 1.]])

• zeros()函数，创建一个元素全部为0的数组

np.zeros(shape,dtype=数据类型)#dtype可以省略

>>> np.zeros((2,3))
array([[0., 0., 0.],
       [0., 0., 0.]])

• eye()函数：创建一个单位矩阵这里shape只需要写内容，不需要再有一个()

np.eye(shape)#这里shape只需要写内容，不需要再有一个()


>>> np.eye(3)
array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
>>> np.eye(2,3)
array([[1., 0., 0.],
       [0., 1., 0.]])

• linspace()函数：创建等差数列；这里不是前闭后开；包括终止数字值

no.linspace(start,stop,num=50)
#开始数字
#结束数字
#元素个数

>>> np.linspace(1,10,10)
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

• logspace()函数：创建一个等比数列

np.logspace(start,stop,num=50,base=10)
#起始指数
#终止指数
#元素个数
#基

#生成数组的第一个值是 基的起始指数次方；
#生成数组的最后一个值是 基的终止指数次方

>>> np.logspace(1,5,5,base=2)
array([ 2.,  4.,  8., 16., 32.])
>>> np.logspace(1,5,5,2)
array([1.e+01, 1.e+02, 1.e+03, 1.e+04, 1.e+05])

• asarray()函数：将列表或元组转化为数组对象

1. 与array()函数类似，也可以将列表和元组转化为数组对象
2. 主要区别是：当数据元本身是数组对象时，array()仍会复制出一个新的数组对象，占用新的内存，而asarray()函数则不会
3. 当数据源本身已经是一个ndarray对象时；array()仍然会复制出一个副本；asarray()则直接引用了本来的数组
   例子1：修改列表时，不会影响数组中的值

>>> import numpy as np
>>> list1=[[1,1,1],[1,1,1],[1,1,1]]
>>> arr1=np.array(list1)
>>> arr2=np.asarray(list1)
>>>
>>> list1[0][0] = 3
>>> print('list1:\n',list1)
list1:
 [[3, 1, 1], [1, 1, 1], [1, 1, 1]]
>>> print('arr1:\n',arr1)
arr1:
 [[1 1 1]
 [1 1 1]
 [1 1 1]]
>>> print('arr2:\n',arr2)
arr2:
 [[1 1 1]
 [1 1 1]
 [1 1 1]]

例子2：修改列表时，不会影响数组中的值

import numpy as np
arr1=np.ones((3,3))
arr2=np.array(arr1)
arr3=np.asarray(arr1)

arr1[0][0] = 3

print('arr1:\n',arr1)
print('arr2:\n',arr2) 
print('arr3:\n',arr3)

例子2输出结果为：

arr1:
 [[3. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
arr2:
 [[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
arr3:
 [[3. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

5.3 数组运算

5.3.1 数据运算1

5.3.1.1 数据元素的切片

5.3.1.1.1 二维数组

使用数组记得导入numpy库
定义一个二维数组

>>> import NumPy as np
Traceback (most recent call last):
ModuleNotFoundError: No module named 'NumPy'
>>> b = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

对一个维度进行切片

>>> b[0]
array([0, 1, 2, 3])
>>> b[0:2]
array([[0, 1, 2, 3],
       [4, 5, 6, 7]])
>>> b[:2]
array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

对两个维度同时进行切片

>>> b[0:2,0:2]
array([[0, 1],
       [4, 5]])
>>> b[0:2,1:3]
array([[1, 2],
       [5, 6]])
>>> b[:,0]
array([0, 4, 8])#这里是一个向量，也就是一个一行三列的数组，而不是三行一列的数组

5.3.1.1.2 三维数组

>>> t = np.array([[[0,1,2,3],[4,5,6,7],[8,9,10,11]],[[12,13,14,15],[16,17,18,19],[20,21,22,23]]])
>>> t
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> t[:,:,0]
array([[ 0,  4,  8],
       [12, 16, 20]])
>>> t[:,:,1]
array([[ 1,  5,  9],
       [13, 17, 21]])

5.3.1.2 改变数组的形状

函数	功能描述
np.reshape(shape)	不改变当前数组，按照shape创建新的数组
np.resize(shape)	改变当前数组，按照shape创建数组

例子：

#定义一个十二个数的序列
>>> b = np.arange(12)
>>> b
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

#使用reshape()函数按照shape创建新的数组，没有改变当前数组b
>>> b.reshape(3,4)
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> b
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

#使用resize()函数按照shape改变了当前数组b
>>> b.resize(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

• 当改变形状时，应该考虑到数组中元素的个数，确保改变前后，元素总个数相等。
  例子：

>>> b = np.arange(12)
>>> b
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])
>>> b.reshape(2,5)#这里由于2*5等于10≠12，所以会出现错误提示
Traceback (most recent call last):
  File "", line 1, in <module>
ValueError: cannot reshape array of size 12 into shape (2,5)

5.3.1.3 创建数组并且改变数组的形状

>>> b = np.arange(12)
>>> b.reshape(3,4)
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> b
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

• 使用下面的方法可以快速创建指定形状的矩阵
  创建二维数组的例子

>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

创建三维数组的例子

>>> t = np.arange(24).reshape(2,3,4)
>>> t
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

5.3.1.4 reshape()函数中的参数为-1

• 可以把shape中某一个维度的值设置为-1
• 根据数组中元素总个数，以及其他维度的取值，来自动计算出这个维度的取值

np.reshape(shape)#可以把shape中某一个维度的值设置为-1

例如

>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> b.reshape(-1,1)#-1表示系统自动计算
array([[ 0],
       [ 1],
       [ 2],
       [ 3],
       [ 4],
       [ 5],
       [ 6],
       [ 7],
       [ 8],
       [ 9],
       [10],
       [11]])#这不是一维数组，而是一个12*1的二维数组

#使用reshape函数把上述12*1的二维数组改变为一维数组
>>> b.reshape(-1)
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

5.3.1.5 数组间的运算

5.3.1.5.1 数组的加法运算

• 将数组对应的数字相加
• 数组间的元素个数不相同，无法相加

>>> a = np.array([0,1,2,3])
>>> d = np.array([2,3,4,5])
>>> a+d
array([2, 4, 6, 8])

• 一维数组可以和多维数组相加，相加时会将一维数组扩展至多维。
  例如

>>> a = np.array([0,1,2,3])
>>> b = np.array([[0,1,2,3],[4,5,6,7],[8,9,10,11]])
>>> a+b
array([[ 0,  2,  4,  6],
       [ 4,  6,  8, 10],
       [ 8, 10, 12, 14]])

• 数组之间的减法、乘法、除法运算，和加法运算规则相同
• 当两个数组中元素的数据类型不同时，精度低的数据类型，会自动转换为精度更高的数据类型，然后再进行运算。

5.3.1.5.2 数组间的幂运算

幂运算：对数组中的每个元素求n次方

>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> b **2
array([[  0,   1,   4,   9],
       [ 16,  25,  36,  49],
       [ 64,  81, 100, 121]], dtype=int32)

二维数组就是矩阵，是一种非常常用的数据组织形式

5.3.1.6 矩阵运算

5.3.1.6.1 矩阵乘法

• 乘号运算符：矩阵中对应的元素分别相乘
  例如：

>>> A = np.array([[1,1],[0,1]])
>>> B = np.array([[2,0],[3,4]])
>>> C = A * B
>>> C
array([[2, 0],
       [0, 4]])

• 矩阵相乘：按照矩阵相乘的规则运算

使用NumPy库中的matmul()函数和dot()函数

>>> np.matmul(A,B)
array([[5, 4],
       [3, 4]])
>>> np.dot(A,B)
array([[5, 4],
       [3, 4]])

5.3.1.6.2 转置和求逆

• 矩阵转置：np.transpose()
• 矩阵求逆：np.linalg.inv()

>>> A = np.array([[1,1],[0,1]])
>>> B = np.array([[2,0],[3,4]])
>>> A
array([[1, 1],
       [0, 1]])
>>> B
array([[2, 0],
       [3, 4]])
#对A、B分别求转置
>>> np.transpose(A)
array([[1, 0],
       [1, 1]])
>>> np.transpose(B)
array([[2, 3],
       [0, 4]])
#对A、B分别求逆
>>> np.linalg.inv(A)
array([[ 1., -1.],
       [ 0.,  1.]])
>>> np.linalg.inv(B)
array([[ 0.5  ,  0.   ],
       [-0.375,  0.25 ]])

5.3.2 数组运算2（数组元素之间的运算）

5.3.2.1 数组间的运算

函数	功能描述
numpy.sum()	计算所有元素的和
numpy.prod()	计算所有元素的乘积
numpy.diff()	计算数组的相邻元素之间的差
np.sqrt()	计算各元素的平方根
np.exp()	计算各元素的指数值
np.abs()	取各元素的绝对值

5.3.2.1.1 求和函数：sum()

• 对数组中的所有的元素求和

#对一维数组求和
>>> a = np.arange(4)
>>> a
array([0, 1, 2, 3])
>>> np.sum(a)
6

#对二维数组求和
>>> b = np.arange(12).reshape(3,4)
>>> b
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> np.sum(b)
66

• 如何按行或者按列求和？

1. 需要用到sum()函数中的第二个参数轴；
2. 轴（axes）：数组中的每一个维度被称为一个轴，（高，列，行
   ）
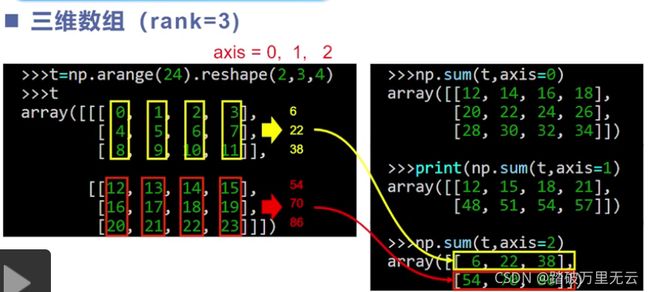
3. 秩（rank）：轴的个数，维度的个数
4. 对于第二个参数的选择sum(A,axis=v)函数，数字0代表着最高维，与reshaple()函数成(0，1，2)的对应关系
5. 求和结果就是把asix那个维数去掉之后的矩阵形状。

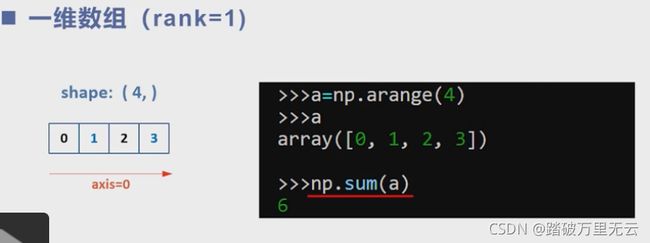
先来看一维数组，形状是shape:(4,)，轴等于0，对它使用sum()函数，就是把这个轴上的四个元素相加，相加后的结果中这个轴就消失了，收缩成了一个点，从一位数组变成了一个数字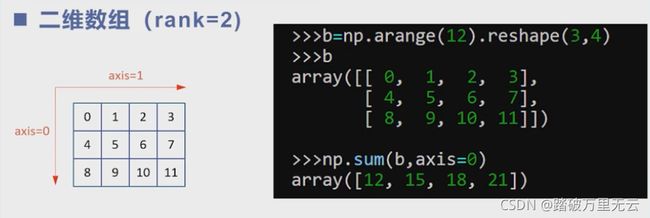

对于二维数组，第一个维度维度上轴等于0，第二个维度上轴等于1，当执行如下代码轴等于0时，应该是将这个轴上所有三个元素相加，相加后这个元素就消失了，得到的四个数字就是结果，是一个一维数组；当执行数字等于1时，将行上的数字相加；

对于三维数组，轴从小到大对应着高维到低维

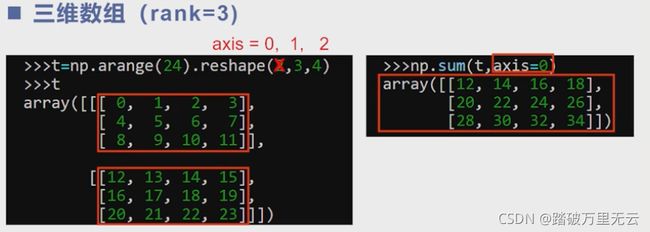
5.3.2.1.2 求积函数：prod()

用法和sum()函数一摸一样

5.3.2.1.3 等函数：一些例子

>>> d = np.logspace(1,4,4,base=2)
>>> d
array([ 2.,  4.,  8., 16.])
>>> np.sqrt(d)
array([1.41421356, 2.        , 2.82842712, 4.        ])

5.3.2.2 数组的”堆叠“

5.3.2.2.1 一维数组的”堆叠“

将一些低维组成高维数组，使用函数np.stack()
语法如下：

np.stack((数组1,数组2,...),axis)
#参数的第一部分是待堆叠的数组
#参数的第二部分是指定堆叠时使用的轴

• 对于两个一维数组x和y，要把它们堆叠为二维数组，有两种方式

1. 在axis=0轴0上堆叠，堆叠后新出现的轴是第一个轴，这两个数组本身的形状就是shape:(3,)，堆叠后形成的二维数组，形状是shape:(2,3)
2. 在axis=1轴1上堆叠，堆叠后新出现的轴是第二个轴，二维数组的形状应该是shape:(3,2)
   
   程序验证：

>>> x = np.array([1,2,3]) #创建一维数组x
>>> y = np.array([4,5,6]) #创建一维数组y
>>> x
array([1, 2, 3])
>>> y
array([4, 5, 6])
>>> np.stack((x,y),axis=0) #首先在轴=0上堆叠
array([[1, 2, 3],
       [4, 5, 6]])
>>> np.stack((x,y),axis=1) #首先在轴=1上堆叠
array([[1, 4],
       [2, 5],
       [3, 6]])

5.3.2.2.1 二维数组的”堆叠“

>>> m = np.array([[1,2,3],[4,5,6],[7,8,9]])
>>> n = np.array([[10,20,30],[40,50,60],[70,80,90]])
>>> m
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
>>> n
array([[10, 20, 30],
       [40, 50, 60],
       [70, 80, 90]])
>>> m.shape
(3, 3)
>>> n.shape
(3, 3)


>>> np.stack((m,n),axis=0).shape#在轴0上堆叠
(2, 3, 3)
>>> np.stack((m,n),axis=1).shape#在轴1上堆叠
(3, 2, 3)
>>> np.stack((m,n),axis=2).shape#在轴2上堆叠
(3, 3, 2)

5.4 矩阵和随机数

上节回顾：

• 每个数组都是一个ndarray对象
• 数组中的元素数据类型相同
• 数组中的元素下标从0开始
• 数组对象的常用属性：维数、形状、数据类型等。

5.4.1 矩阵–numpy.matrix

5.4.1.1 矩阵的创建

matrix(字符串/列表/元组/数组)
mat(字符串/列表/元组/数组)#简写

创建矩阵两种方式的例子

>>> a = np.mat('1 2 3;4 5 6')
>>> a
matrix([[1, 2, 3],
        [4, 5, 6]])


>>> b = np.mat([[1,2,3],[4,5,6]])
>>> b
matrix([[1, 2, 3],
        [4, 5, 6]])

借助NumPy二维数组创建矩阵

>>> a = np.array([[1,2,3],[4,5,6]])
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>> m = np.mat(a)
>>> m
matrix([[1, 2, 3],
        [4, 5, 6]])
>>> type(a)
<class 'numpy.ndarray'>
>>> type(m)
<class 'numpy.matrix'>

5.4.1.2 矩阵对象的属性

属性	说明
.ndim	矩阵的维数
.shape	矩阵的形状
.size	矩阵的元素个数
.dtype	元素的数据类型

>>> m
matrix([[1, 2, 3],
        [4, 5, 6]])
>>> m.ndim
2
>>> m.dtype
dtype('int32')
>>> m.shape
(2, 3)
>>> m.size
6

5.4.1.3 矩阵运算

5.4.1.3.1 矩阵相乘

>>> a1 = np.mat([[0,1],[2,3]])
>>> a2 = np.mat([[1,1],[2,0]])
>>> a1
matrix([[0, 1],
        [2, 3]])
>>> a2
matrix([[1, 1],
        [2, 0]])
>>> a3 = a1 * a2
>>> a3
matrix([[2, 0],
        [8, 2]])

5.4.1.3.2 矩阵转置、求逆

• 矩阵转置：.T
• 矩阵求逆：.I
• 注意，这里都是大写的

>>> n = np.mat([[1,2],[-1,-3]])
>>> n
matrix([[ 1,  2],
        [-1, -3]])
>>> n.T
matrix([[ 1, -1],
        [ 2, -3]])
>>> n.I
matrix([[ 3.,  2.],
        [-1., -1.]])
>>> n*n.I
matrix([[1., 0.],
        [0., 1.]])

5.4.1.3.3 非方阵的转置、求逆运算

也可以

>>> a = np.array([[1,2,3],[4,5,6]])
>>> m = np.mat(a)
>>> m
matrix([[1, 2, 3],
        [4, 5, 6]])
>>> m.T
matrix([[1, 4],
        [2, 5],
        [3, 6]])
>>> m.I
matrix([[-0.94444444,  0.44444444],
        [-0.11111111,  0.11111111],
        [ 0.72222222, -0.22222222]])
>>> m*m.I
matrix([[ 1.0000000e+00, -4.4408921e-16],
        [ 0.0000000e+00,  1.0000000e+00]])

5.4.1.3.4 数组和矩阵通用时，尽量数组

5.4.2 随机数

5.4.2.1 随机数模块-numpy.random

函数	功能描述	返回值
np.random.rand(d0,d1,…,dn)	元素在[0,1]区间均匀分布的数组；d0~dn是数组形状	浮点数；参数空返回一个数字；
np.random.uniform(low,hige,size)	元素在[low,hige)区间均匀分布的数组；size是数组的形状	浮点数
numpy.random.randint(low,hige,size)	元素在[low,hige)区间均匀分布的数组	整数
np.random.randn(d0,d1,…,dn)	产生标准正态分布的数组	浮点数
np.random.normal(loc,scale,size)	产生正态分布的数组；loc是均值；scale是标准差	浮点数

例如：
创建2*3的随机数组，取值是在[0,1]之间均匀分布的浮点数
参数为空，返回一个数字

# 创建2*3的随机数组，取值是在[0,1]之间均匀分布的浮点数
>>> np.random.rand(2,3)
array([[0.86141698, 0.6138186 , 0.06648614],
       [0.03880645, 0.13625046, 0.37195718]])

#参数为空，返回一个数字
>>> np.random.rand()
0.8324939573755401

再例如：
创建3*2的随机数组，取值是在1至5之间均匀分布的浮点数

#创建3*2的随机数组，取值是在1至5之间均匀分布的浮点数
>>> np.random.uniform(1,5,(3,2))
array([[2.6016163 , 2.12817905],
       [4.82779385, 4.04064114],
       [1.89608031, 4.7236666 ]])

再如
创建2*3的随机数组，取值是在1至5之间的均匀分布的整数

# 创建2*3的随机数组，取值是在1至5之间的均匀分布的整数
>>> np.random.randint(1,5,(3,2))
array([[3, 1],
       [4, 4],
       [1, 2]])

创建2*3的随机数组，符合标准正态分布

#创建2*3的随机数组，符合标准正态分布
>>> np.random.randn(2,3)
array([[ 0.47533113,  1.74033136, -0.92451441],
       [-0.7392184 ,  2.92768514, -0.1467677 ]])

创建3*2的随机数组，符合正态分布，均值为0，方差为1

#创建3*2的随机数组，符合正态分布，均值为0，方差为1
>>> np.random.normal(0,1,(3,2))
array([[-1.27922759, -0.49258568],
       [ 1.10361138,  0.44144055],
       [ 1.92877588, -0.38763335]])

对于随机数，同样的语句执行有不同的结果

5.4.2.2 伪随机数

• 伪随机数：由随机种子，根据一定的算法生成的
• 随机种子：指定随机数生成时所用算法开始的整数值。

1. 如果使用相同的seed()值，则每次生成的随机数都相同。
2. 如果不设置这个值，则系统根据时间来自己选择这个值，此时每次生成的随机数因时间差异而不同。随机种子来源于系统时钟。
3. 随机数产生的算法和系统有关
4. 采用seed()函数设置随机种子，仅一次有效

5.4.2.2.1 seed()函数

• 采用seed()函数设置的随即种子仅一次有效

>>> np.random.rand(2,3)
array([[0.14347163, 0.49589878, 0.95454587],
       [0.13751674, 0.85456667, 0.42853136]])


>>> np.random.seed(612)
>>> np.random.rand(2,3)# 这两次产生的随机数是一样的
array([[0.14347163, 0.49589878, 0.95454587],
       [0.13751674, 0.85456667, 0.42853136]])


>>> np.random.rand(2,3)
array([[0.36969445, 0.94758214, 0.09295099],
       [0.66035565, 0.84156851, 0.90694096]])

5.4.2.3 打乱顺序函数

• 在机器学习神经网络的编程中，防止过拟合，往往会打乱数据顺序
• 形象的称为洗牌函数
• 每次执行这个代码，都会重新打乱元素顺序，得到不同的运行结果

np.random.shuffle(序列/python列表/数组)

例如：

>>> arr = np.arange(10)
>>> print(arr)
[0 1 2 3 4 5 6 7 8 9]
>>> np.random.shuffle(arr)#每次执行这个代码，都会重新打乱数组元素，得到不同的运行结果
>>> print(arr)
[7 2 8 4 9 6 5 0 1 3]

• 对于多维数组，默认只打乱第一维的数组，只有行的位置变化

>>> b = np.arange(12).reshape(4,3)
>>> b
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])
>>> np.random.shuffle(b)
>>> b
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 9, 10, 11],
       [ 6,  7,  8]])