机器学习基础-最优化方法梯度下降

最优化方法-梯度下降

这是机器学习基础的第五篇，本文主要的学习内容为最优化方法即梯度下降：

• 梯度下降： 实现梯度下降、线性回归中的梯度下降
• 随机梯度下降：相关代码调用即可

1.前言： 机器学习方法论

之前已经学习了分类算法：KNN算法，回归算法：线性回归，从这些算法中可以知道：

机器学习就是需要找到一个函数f(x)并进行优化，且这种函数能够进行做预测、分类、生成等工作。

就如何找到函数f(x)的方法论可以得出机器学习的“三把斧”：

• First: 定义一个函数集合 define a function set
• Second: 判断函数的好坏 goodness of a function
• Third: 选择最好的函数 pick the best function
  梯度下降则是用来解决第三步，即如何找到最好的函数，让损失函数最小化。
  梯度下降（Gradient Descent, GD）并不是一个机器学习算法，而是一种基于搜索的最优化方法，其作用是用来对原始的损失函数进行优化，找到最优的参数使得损失函数值最小。通过导数告诉我们此时此刻某参数应该朝什么方向，以怎样的速度运动，能安全高效降低损失值，朝最小损失值靠拢。

2.什么是梯度

多元函数的导数(derivative)就是梯度(gradient)，分别对每个变量进行微分，然后用逗号分割开，梯度是用括号包括起来，说明梯度其实一个向量，我们说损失函数L的梯度为：
$$\Delta f=(\frac{\alpha L}{\alpha x_1},\frac{\alpha L}{\alpha x_2})$$
梯度就是向量，和参数维度一样。假设有一个二元函数$f(x1,x2)=x_1^2+x_1{x}_2-3x_2$, 它的梯度为：
$\Delta f=(\frac{\alpha L}{\alpha x_1},\frac{\alpha L}{\alpha x_2})$ =$(2x_1+x_2,x_1-3)$
在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向 。
梯度指向误差值增加最快的方向，导数为0（梯度为0向量）的点，就是优化问题的解。在上面的二元函数中，点(1,2)向着(4,2)的方向就是梯度方向 为了找到这个解，我们沿着梯度的反方向进行线性搜索，从而减少误差值。每次搜索的步长为某个特定的数值，直到梯度与0向量非常接近为止。更新的点是所有点的x梯度，所有点的y梯度

3.理解梯度下降计算

梯度下降就可以理解为下山的过程，即从山顶找到一条最短的路到达山谷最低的地方

假设只移动一步的话，我们可以根据求导的公式得到下一步的落脚点的迭代公式：

为什么要梯度要乘以一个负号？

我们已经知道：梯度的方向就是损失函数值在此点上升最快的方向，是损失增大的区域，而我们要使损失最小，因此就要逆着梯度方向走，自然就是负的梯度的方向，所以此处需要加上负号

关于参数$\eta$ :

我们已经知道，梯度对应的是下山的方向，而参数 $\eta$对应的是步伐的长度。在学术上，我们称之为“学习率”(learning rate)，是模型训练时的一个很重要的超参数，能直接影响算法的正确性和效率：
首先，学习率$\eta$不能太大。因此从数学角度上来说，一阶泰勒公式只是一个近似的公式，只有在学习率很小，也就是$\Delta a$$\Delta b$很小时才成立。并且从直观上来说，如果学习率太大，那么有可能会“迈过”最低点，从而发生“摇摆”的现象（不收敛），无法得到最低点
其次，学习率$\eta$又不能太小。如果太小，会导致每次迭代时，参数几乎不变化，收敛学习速度变慢，使得算法的效率降低，需要很长时间才能达到最低点。

4.存在的问题

梯度算法有一个比较致命的问题：
从理论上，它只能保证达到局部最低点，而非全局最低点。在很多复杂函数中有很多极小值点，我们使用梯度下降法只能得到局部最优解，而不能得到全局最优解。那么对应的解决方案如下：首先随机产生多个初始参数集，即多组$a_0,b_0$；然后分别对每个初始参数集使用梯度下降法，直到函数值收敛于某个值；最后从这些值中找出最小值，这个找到的最小值被当作函数的最小值。当然这种方式不一定能找到全局最优解，但是起码能找到较好的。

5.手动实现梯度下降

python中有两种常见求导的方法，一种是使用Scipy库中的derivative方法，另一种就Sympy库中的diff方法。

scipy.misc.derivative(func, x0, dx=1.0, n=1, args=(), order=3)[source]

在一个点上找到函数的第n个导数。即给定一个函数，即使用间距为dx的中心差分公式来计算x0处的第n个导数。
参数：

• func：需要求导的函数，只写参数名即可，不要写括号，否则会报错
• x0：要求导的那个点，float类型
• dx（可选）：间距，应该是一个很小的数，float类型
• n（可选）：n阶导数。默认值为1，int类型
• args（可选）：参数元组
• order（可选）：使用的点数必须是奇数，int类型

举例

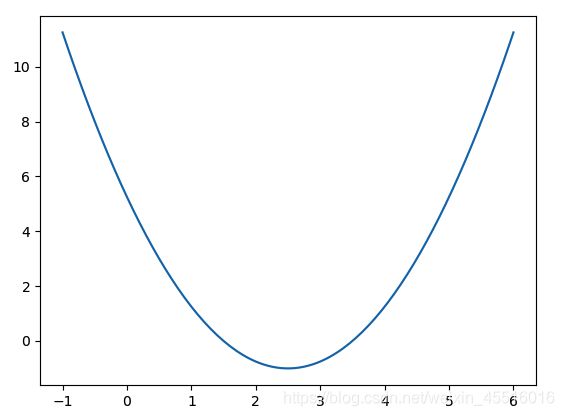
首先构造一个损失函数$loss(x)=(x-2.5{)}^2-1$ ，然后创建在-1到6的范围内构建140个点，并且求出对应的损失函数值，这样就可以画出损失函数的图形。

import numpy as np
import matplotlib.pyplot as plt
from scipy.misc import derivative

def lossFunction(x):
    return (x-2.5)**2-1

# 在-1到6的范围内构建140个点
plot_x = np.linspace(-1,6,141)
# plot_y 是对应的损失函数值
plot_y = lossFunction(plot_x)

plt.plot(plot_x,plot_y)
plt.show()

算法：计算损失函数J在当前点的对应导数
输入：当前数据点theta
输出：点在损失函数上的导数
接下来我们就可以进行梯度下降的操作了。首先我们需要定义一个点$\Theta$ 作为初始值，正常应该是随机的点，但是这里先直接定为0。然后需要定义学习率 ，也就是每次下降的步长$\eta$。这样的话，点$\Theta$ 每次沿着梯度的反方向移动$\eta$ 距离，即$\Theta =\Theta -\eta \ast \Delta f$，然后循环这一下降过程。
那么还有一个问题：如何结束循环呢？梯度下降的目的是找到一个点，使得损失函数值最小，因为梯度是不断下降的，所以新的点对应的损失函数值在不断减小，但是差值会越来越小，因此我们可以设定一个非常小的数作为阈值，如果说损失函数的差值减小到比阈值还小，我们就认为已经找到了。

def dLF(theta):
    return derivative(lossFunction, theta, dx=1e-6)

theta = 0.0
eta = 0.1
epsilon = 1e-6
while True:
    # 每一轮循环后，要求当前这个点的梯度是多少
    gradient = dLF(theta)
    last_theta = theta
    # 移动点，沿梯度的反方向移动步长eta
    theta = theta - eta * gradient
    # 判断theta是否达到最小值
    # 因为梯度在不断下降，因此新theta的损失函数在不断减小
    # 看差值是否达到了要求
    if(abs(lossFunction(theta) - lossFunction(last_theta)) < epsilon):
        break
print(theta)
print(lossFunction(theta))

"""
输出：
2.498732349398569
-0.9999983930619527
"""

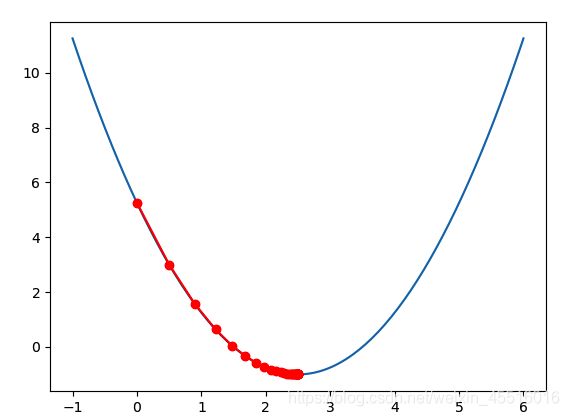
接下来把梯度下降封装成函数并画图展示：

def gradient_descent(initial_theta, eta, epsilon=1e-6):
    theta = initial_theta
    theta_history.append(theta)
    while True:
        # 每一轮循环后，要求当前这个点的梯度是多少
        gradient = dLF(theta)
        last_theta = theta
        # 移动点，沿梯度的反方向移动步长eta
        theta = theta - eta * gradient
        theta_history.append(theta)
        # 判断theta是否达到损失函数最小值的位置
        if(abs(lossFunction(theta) - lossFunction(last_theta)) < epsilon):
            break

def plot_theta_history():
    plt.plot(plot_x,plot_y)
    plt.plot(np.array(theta_history), lossFunction(np.array(theta_history)), color='red', marker='o')
    plt.show()

6. 线性回归中的梯度下降

在多元线性回归中使用梯度下降法求损失函数的最小值（求导），并且使用向量化的方式进行编写代码。
举例：
在多元线性回归中，其预测值为： $y_{(}i)={\Theta }_0+{\Theta }_1{X}_1^i+{\Theta }_2{X}_2^i$
已知训练数据样本x,y, 找到${\Theta }_0，{\Theta }_1...{\Theta }_n$使得损失函数尽可能小：

整理之后可得下列式子：

将上式中的预测函数改写成向量点乘的形式：

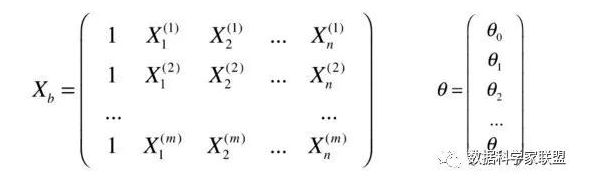
损失函数提取为：

通过对梯度取平均值，为了除去样本数量对结果的影响，最终得到梯度结果为：

实现梯度下降的代码

def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
    """根据训练数据集X_train, y_train, 使用梯度下降法训练Linear Regression模型"""
    assert X_train.shape[0] == y_train.shape[0], \
        "the size of X_train must be equal to the size of y_train"

    def J(theta, X_b, y):
        try:
            return np.sum((y - X_b.dot(theta)) ** 2) / len(y)
        except:
            return float('inf')
        
    def dJ(theta, X_b, y):
        return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

    def gradient_descent(X_b, y, initial_theta, eta, n_iters=1e4, epsilon=1e-8):

        theta = initial_theta
        cur_iter = 0

        while cur_iter < n_iters:
            gradient = dJ(theta, X_b, y)
            last_theta = theta
            theta = theta - eta * gradient
            if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
                break

            cur_iter += 1

        return theta

    X_b = np.hstack([np.ones((len(X_train), 1)), X_train])
    initial_theta = np.zeros(X_b.shape[1])
    self._theta = gradient_descent(X_b, y_train, initial_theta, eta, n_iters)

    self.intercept_ = self._theta[0]
    self.coef_ = self._theta[1:]

    return self

调用该函数，

lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train, y_train, )
lin_reg2.coef_
"""
输出：
array([nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan,nan])
"""

上面的结果为空，因为数据规格有大有小，在梯度下降之前进行数据归一化

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)
X_train_std = standardScaler.transform(X_train)
lin_reg3 = LinearRegression()
lin_reg3.fit_gd(X_train_std, y_train)
X_test_std = standardScaler.transform(X_test)
lin_reg2.score(X_test, y_test)
"""
输出：
0.8129802602658466
"""

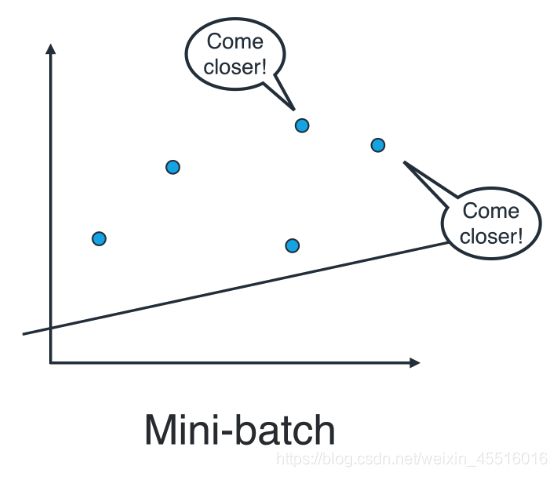
7.批量梯度下降和随机梯度下降

• 随机梯度下降(Stochastic): 逐个地在每个数据点应用均方（或绝对）误差，并重复这一流程很多次。
  
• 批量梯度下降法: 同时在每个数据点应用均方（或绝对）误差，并重复这一流程很多次。
  
  实际上，在大部分情况下，两种都不用。思考以下情形：如果你的数据十分庞大，两种方法的计算速度都将会很缓慢。线性回归的最佳方式是将数据拆分成很多小批次。每个批次都大概具有相同数量的数据点。然后使用每个批次更新权重。这种方法叫做小批次梯度下降法。
  

在SKlearn中实现线性回归

对于你的线性回归模型，将使用 scikit-learn 的 LinearRegression 类。此类会提供函数 fit() 来将模型与数据进行拟合。

>>> from sklearn.linear_model import LinearRegression
>>> model = LinearRegression()
>>> model.fit(x_values, y_values)
>>> model.predict(sample) 

# 若为多项式的形式，degree=2表示建立datasets_X的二 次多项式特征X_poly。
poly_reg =PolynomialFeatures(degree=2)
X_ploy =poly_reg.fit_transform(datasets_X)
lin_reg_2=linear_model.LinearRegression()
lin_reg_2.fit(X_ploy,datasets_Y)

[参考文献]
还不了解梯度下降法？看完这篇就懂了
手动实现梯度下降
线性回归中的梯度下降