sklearn多元线性回归预测房价
- 多元线性回归
-
-
- 一.excel
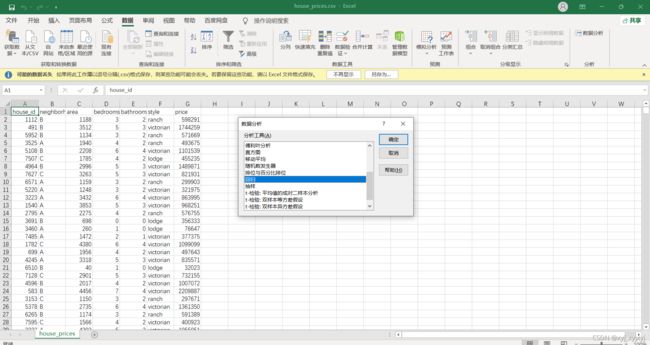
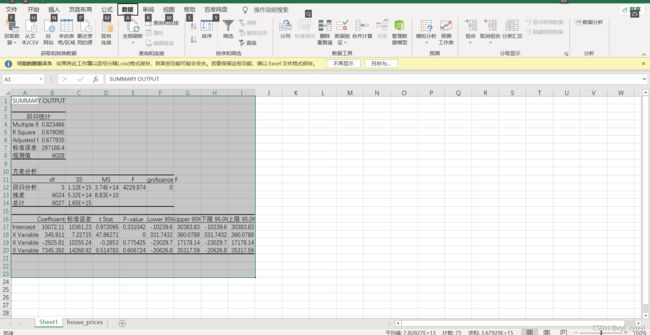
- 1.加入应用模型
- 2.对数据进行清洗后再求解
- 3.原数据相关性矩阵
- 4.Z方法处理的数据相关性矩阵
- 5.IQR方法处理的数据相关性矩阵
多元线性回归
一.excel
import pandas as pd
import numpy as np
import math
import matplotlib.pyplot as plt # 画图
from sklearn import linear_model # 线性模型
data = pd.read_csv('D:/EdgeDownload/house_prices.csv') #读取数据
data.head() #数据展示
| house_id |
neighborhood |
area |
bedrooms |
bathrooms |
style |
price |
| 1112 |
B |
1188 |
3 |
2 |
ranch |
598291 |
| 491 |
B |
3512 |
5 |
3 |
victorian |
1744259 |
| 5952 |
B |
1134 |
3 |
2 |
ranch |
571669 |
| 3525 |
A |
1940 |
4 |
2 |
ranch |
493675 |
| 5108 |
B |
2208 |
6 |
4 |
victorian |
1101539 |
1.加入应用模型
# 应用模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
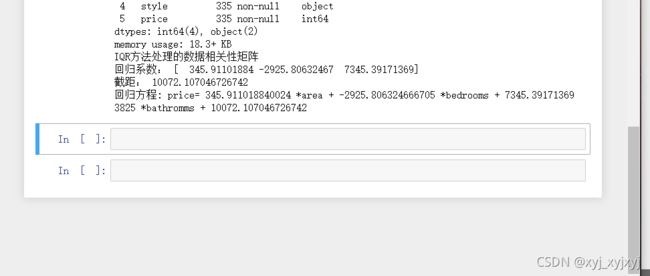
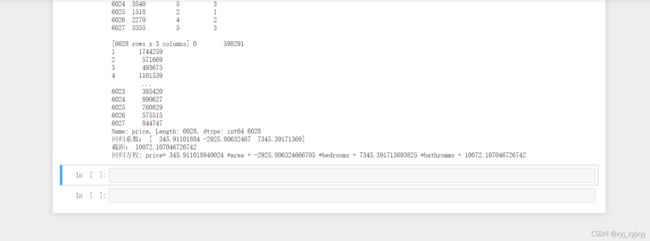
print("回归系数:", model.coef_)
print("截距:", model.intercept_)
print('回归方程: price=',model.coef_[0],'*area +',model.coef_[1],'*bedrooms +',model.coef_[2],'*bathromms +',model.intercept_)
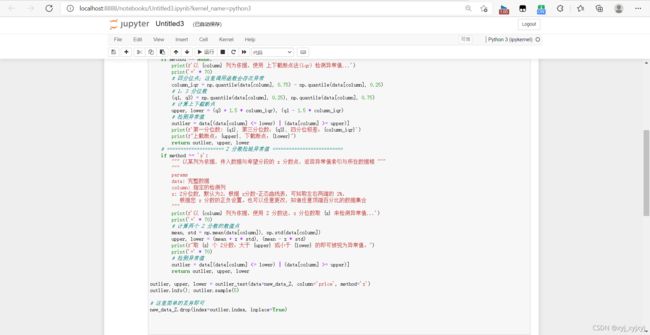
2.对数据进行清洗后再求解
new_data_Z=new_data.iloc[:,0:]
new_data_IQR=new_data.iloc[:,0:]


3.原数据相关性矩阵
print("原数据相关性矩阵")
new_data.corr()

4.Z方法处理的数据相关性矩阵
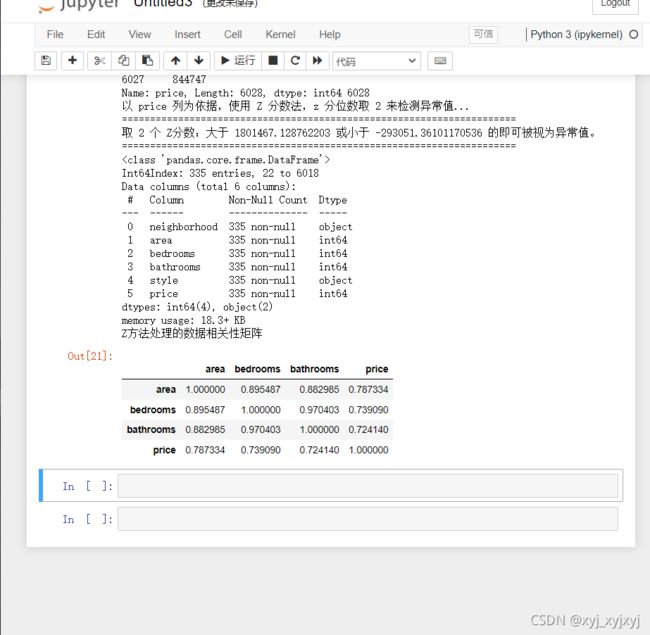
print("Z方法处理的数据相关性矩阵")
new_data_Z.corr()
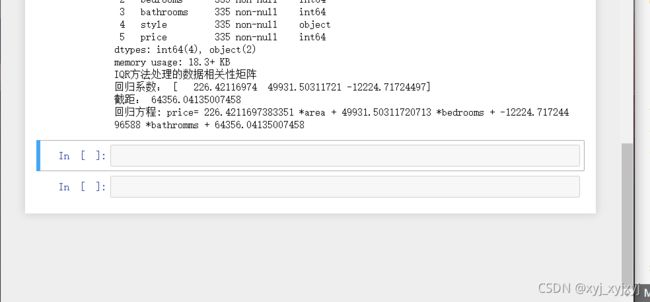
5.IQR方法处理的数据相关性矩阵
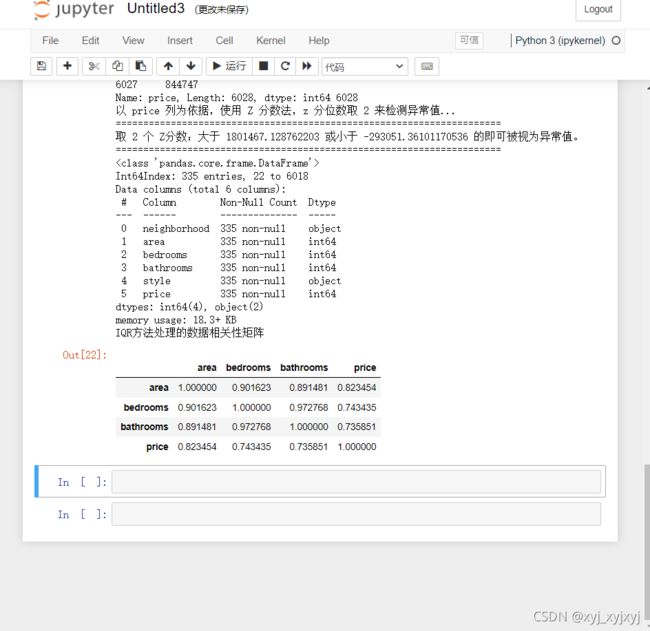
print("IQR方法处理的数据相关性矩阵")
new_data_IQR.corr()
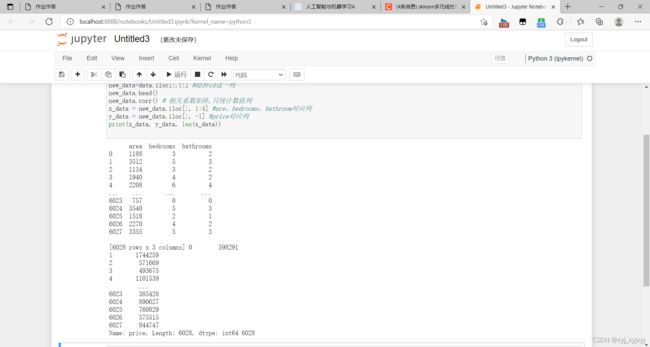
x_data = new_data_Z.iloc[:, 1:4]
y_data = new_data_Z.iloc[:, -1]
# 应用模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
print("回归系数:", model.coef_)
print("截距:", model.intercept_)
print('回归方程: price=',model.coef_[0],'*area +',model.coef_[1],'*bedrooms +',model.coef_[2],'*bathromms +',model.intercept_)
x_data = new_data_IQR.iloc[:, 1:4]
y_data = new_data_IQR.iloc[:, -1]
# 应用模型
model = linear_model.LinearRegression()
model.fit(x_data, y_data)
print("回归系数:", model.coef_)
print("截距:", model.intercept_)
print('回归方程: price=',model.coef_[0],'*area +',model.coef_[1],'*bedrooms +',model.coef_[2],'*bathromms +',model.intercept_)