3D 点云形状特征的二维主流形描述 论文笔记 2020-9-29

3D 点云形状特征的二维主流形描述

关键词

形状特征；二维主流形；网格优化逼近；ICNP；三维检索

解决的问题

三维模型缺乏语义层的描述，故三维形状的特征描述方法成为极具挑战性的难题

原理

针对三维点云模型空间分布不均匀且无序的特征,首先构造其二维主流形,并以与球同胚的封闭网格形式给出主流形的二次曲面优化逼近,将三维点云模型的形状描述问题转换为球参数域上分布均匀、沿参数方向有序的二维主流形的参数化网格形状描述问题;然后,对二维主流形的参数化曲面网格进行三维平移、旋转和缩放等基本几何变换,对齐两个曲面流形网格的极轴,作为初始粗对齐;最后,基于迭代最近法向点(iterative closest normal point,简称 ICNP)方法快速比较两个曲面网格流形,实现精准对齐,并将对齐误差作为两个三维点云模型的形状相似测度。

主流形： 嵌入高维空间的非欧氏低维流形,即点集的非线性主成分和子空间的概括。主流形上的每个点都是该点在原始点集中的局部平均，不同于其他的非线性扩展，主流形具有形式简单、自身一致性、几何解释清晰等特点.
二维主流形：G(λ1,λ2) = {G1(λ1,λ2)，G2(λ1,λ2)，…，Gr(λ1,λ2)}控制生成二维主流形
三维点云模型输入的点集合P = {pi，i=1，2，…，m}

主要算法如下：
Step 1.对其进行主成分分析 PCA,得到 P 的第一、第二和第三主轴ψ1,ψ2,ψ3,以 3 个主轴为轴构建椭球面;
Step 2.以ψ3 与椭球的两个交点为极点,以ψ1,ψ2 形成的主椭圆为赤道,以椭球面的经度和纬度方向为参数
(λ1,λ2)的方向,沿(λ1,λ2)进行均匀的 20×20 采样;
Step 3.以 20×20 的采样点为结点集合 V,在采样点间沿参数(λ1,λ2)方向顺次连接,构造边的集合,记作 E,从而
得到封闭的二维主流形的逼近网格 MG,记为 MG={V,E};
Step 4.将 MG 作为初始二维主流形的二次曲面网格逼近,调整 MG 得到优化网格逼近；

优化网格逼近：
初始网格 MG={V,E}
V = {vi,i=1,2,…,t}为MG的结点集合
E={ei,i=1,2,…,t}为MG的无向边集合
设边 ei 的一个相邻边为 ek,则定义结构 Ri={ei,ek},将所有结构的集合记为 R={Ri,i=1,2,…,r}.
给定的三维模型的顶点几何P={pi,i=1,2,…,m}
λiλ1为ei的权重，μi为Ri的权重，wj，λI,μi为常参数

令 U=UY+UE+UR,最小化 U,得到更新后的点集 V。
迭代进行该过程,直到 U 的变化小于给定阈值,此时,图 MG 即为三维模型顶点集合 P 的二维主流形优化逼近.

网格粗对齐：
对于两个主流形的初始网格 MG 和 MG’ :
Step 1. 分别连接它们的两个极点 p1 和 p2、 1 p 和 2 p 作为它们各自的极轴,记为 L 和 L’;
Step 2. 平移主流形网格 MG,使其极点 p1 与 MG’ 的极点 1 p’ 对齐;
Step 3. 旋转主流形网格 MG,使其极轴 L 与 MG’ 的极轴 L’重合;
Step 4. 以 p1 为缩放中心、以 L’/L 为缩放系数对 MG 缩放,使 MG 的极点 p2 与 MG’ 的极点 2 p’重合.
网格ICNP精准对齐：
ICNP 在寻找最近点时考虑法向夹角,迭代过程中利用了更多的几何信息,故所得的对齐结果更加精准

创新点

基于二维主流形的基本理论构造了三维点云模型主流形的曲面逼近网格,从而将空间分布的高度随机和高度不均匀的三维点云集合转换为二维主流形上与球面同胚的空间分布有序的、均匀的规则化参数分布,进而建立三维点云模型的形状特征描述

算法优点

二次主流形是非线性主成分分析方法，可以规避线性降维方法PCA对非线性结构效果差的问题以及受随机扰动影响大的问题，并能够消除高维数据的统计冗余，降低数据信息的损失。

算法缺点

存在少量检索失败的情况，算法计算所得的主流形曲面的亏格总为 0,导致在模型细节信息方面有所丢失,对拓扑分支无法正确描述。

实验结果

如图5，所有的待检索模型均被正确找出

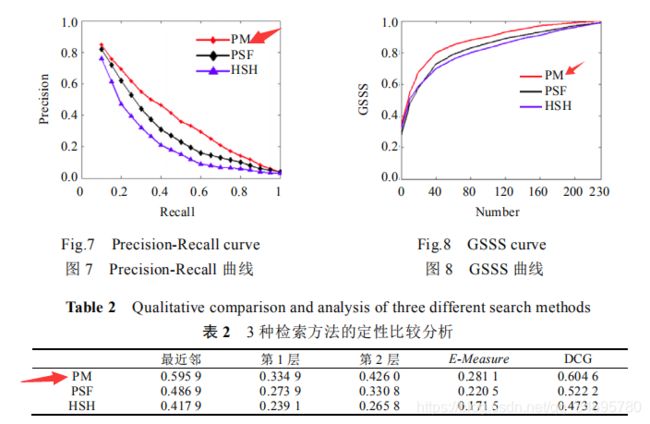
图 7 给出了 3 种算法的 PR(precision-recall)曲线,描述了查准率和查全率之间的关系。(PM)的检索结果要优于另外两种检索,在相同查全率的前提下,PM 算法具有更高的检索精度。
根据图8，PM 算法更能够区分两类模型之间的差异.
从表2来看，PM 方法仍然优于 PSF 方法和 HSH 方法