感知器算法的设计实现 python
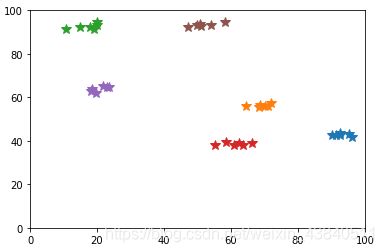
1.数据生成及规范化处理
利用高斯模型,生成 N 类(N>5)数据(2D or 3D),并对生成样本进行规范化处理
mu = np.array([[random.randint(5,95), random.randint(5,95)]])
Sigma = np.array([[8, 5], [3, 2]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(6, 2), R) + mu
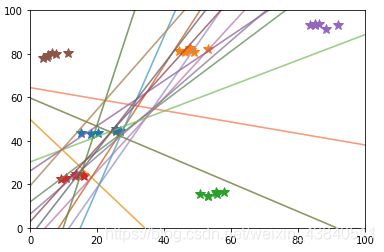
上图即为所有的分界面的图形,但由于无法去除无用的分类面,只能把所有n^2个分类面一一输出
3.生成测试数据列,并对测试数据进行分类判别。
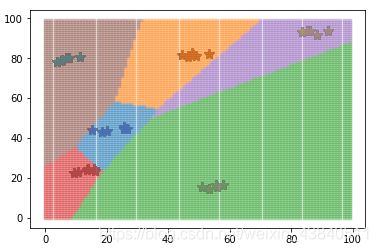
# -*- coding: utf-8 -*-
import random
import copy
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import cholesky
import sys
if __name__ == '__main__':
base = 10.0
data = []
alldata = []
numofN=6
num = 0
while num < numofN:
mu = np.array([[random.randint(5,95), random.randint(5,95)]])#生成随机数据
Sigma = np.array([[8, 5], [3, 2]])
R = cholesky(Sigma)
s = np.dot(np.random.randn(6, 2), R) + mu
key = False
for i in s.tolist():
for j in alldata:
if abs(i[0]-j[0]) + abs(i[1]-j[1]) <=10:
key = True
break
if key:#随机数据碰撞则重来
continue
num += 1
plt.plot(s[:,0],s[:,1],'*',markersize=10)
x = []
for i in s :
x.append(np.array(np.hstack((np.array(i),np.array([base])))))
data.append(np.array(x))
for i in s.tolist():
alldata.append(i)
wlist = []
for i in range(0,numofN) :
wlist.append(np.array([base,base,base]))#初始权向量
ccc=0
while True :
time = 0
for i in range(0,numofN):
for yi in data[i]:
for t in range(0,numofN):
if t == i:
continue
while np.dot(yi,wlist[i]) <= np.dot(yi,wlist[t]) + 0.5:#修正
wlist[i] += np.array(yi)
wlist[t] -= np.array(yi)
time += 1
if time == 0:
break
for i in wlist:
for j in wlist:
if (i==j).all() :
continue
linex = np.array([0.0,100.0])
plt.plot(linex,(((-1)*linex*(i[0]-j[0])-base*(i[2]-j[2]))/(i[1]-j[1])),alpha=0.5) #画分割线
plt.xlim(0,100)
plt.ylim(0,100)
plt.show()
plt.cla()
picx = []
picy = []
for i in range(0,numofN):
picx.append([])
picy.append([])
for i in range(0,100):
for j in range(0,100):
maxx = []
for t in wlist:
maxx.append(np.dot(np.array([i,j,base]),t))
k = maxx.index(max(maxx))
picx[k].append(i)
picy[k].append(j)
for i in data :
plt.plot(i[:,0],i[:,1],'*',markersize=10) #
for i in range(0,numofN):
plt.plot(picx[i],picy[i],'.',alpha=0.3) #画出各个位置上的预测结果