Leetcode 题解 - 数学
Leetcode 题解 - 数学
204. 计数质数
统计所有小于非负整数 n 的质数的数量。(素数的定义很简单,如果一个数如果只能被 1 和它本身整除,那么这个数就是素数。)
输入:n = 10
输出:4
解释:小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
解题思路:如果采用枚举法的话,思路是这样的:
int countPrimes(int n) {
int count = 0;
for (int i = 2; i < n; i++)
if (isPrim(i)) count++;
return count;
}
// 判断整数 n 是否是素数
boolean isPrime(int n) {
for (int i = 2; i < n; i++)
if (n % i == 0)
// 有其他整除因子
return false;
return true;
}
这样写的话时间复杂度 O(n^2),问题很大。
接下来我们介绍一个常见的算法,该算法由希腊数学家厄拉多塞提出,称为厄拉多塞筛法,简称埃氏筛。
首先i不需要遍历到n,而只需要到sqrt(n)即可。为什么呢,我们举个例子,假设n = 12。
12 = 2 × 6
12 = 3 × 4
12 = sqrt(12) × sqrt(12)
12 = 4 × 3
12 = 6 × 2
可以看到,后两个乘积就是前面两个反过来,反转的分界点就在sqrt(n)。换句话说,如果在[2,sqrt(n)]这个区间之内没有发现可整除因子,就可以直接断定n是素数了,因为在区间[sqrt(n),n]也一定不会发现可整除因子。
此外我们考虑这样一个事实:如果 x 是质数,那么大于 x 的 x 的倍数2x,3x,… 一定不是质数,因此我们可以从这里入手。
我们设 isPrime[i] 表示数 i 是不是质数。从小到大遍历每个数,如果这个数为质数,则将其所有的倍数都标记为false(除了该质数本身),这样在运行结束的时候我们即能知道质数的个数。
当然这里还可以继续优化,对于一个质数 x,如果按上文说的我们从 2x 开始标记其实是冗余的,因为 2x,3x,… 这些数一定在 x 之前就被其他数的倍数标记过了,比如i = 4时算法会标记 4 × 2 = 8,4 × 3 = 12 等等数字,但是 8 和 12 已经被i = 2和i = 3的 2 × 4 和 3 × 4 标记过了。我们可以稍微优化一下,让j从i的平方开始遍历
int countPrimes(int n) {
boolean[] isPrim = new boolean[n];
Arrays.fill(isPrim, true);
for (int i = 2; i * i < n; i++)
if (isPrim[i])
for (int j = i * i; j < n; j += i)
isPrim[j] = false;
int count = 0;
for (int i = 2; i < n; i++)
if (isPrim[i]) count++;
return count;
}
最大公约数与最小公倍数
int gcd(int a, int b) {
return b == 0 ? a : gcd(b, a % b);
}
最小公倍数为两数的乘积除以最大公约数。
int lcm(int a, int b) {
return a * b / gcd(a, b);
}
进制转换
504. 七进制数(简单)
给定一个整数,将其转化为7进制,并以字符串形式输出。
输入: 100
输出: "202"
输入: -7
输出: "-10"
注意: 输入范围是 [-1e7, 1e7] 。额外注意对于负数的处理!
class Solution {
public String convertToBase7(int num) {
if(num == 0) return "0";
StringBuilder sb = new StringBuilder();
//判断num是否为负数的标记位
boolean isNegative = num < 0;
if(isNegative) num = - num;
while(num > 0){
sb.append(num % 7);
num /= 7;
}
//回想进制转换的过程,将每次除7的余数倒着相连即可得到转换后的数
String res = sb.reverse().toString();
return isNegative ? '-'+res : res;//注意这里,如果是负数就在前面加负号
}
}
Java 中 static String toString(int num, int radix) 可以将一个整数转换为 radix 进制表示的字符串。
public String convertToBase7(int num) {
return Integer.toString(num, 7);
}
405. 数字转换为十六进制数(简单)
给定一个整数,编写一个算法将这个数转换为十六进制数。对于负整数,我们通常使用 补码运算 方法。
注意:
- 十六进制中所有字母(
a-f)都必须是小写。 - 十六进制字符串中不能包含多余的前导零。如果要转化的数为0,那么以单个字符
'0'来表示;对于其他情况,十六进制字符串中的第一个字符将不会是0字符。 - 给定的数确保在32位有符号整数范围内。
- 不能使用任何由库提供的将数字直接转换或格式化为十六进制的方法。
输入:26
输出:"1a"
输入:-1
输出:"ffffffff"
【笔记】核心思想,使用位运算,每4位,对应1位16进制数字。
- 使用
0xf(00…01111b)获取num的低4位。 - 因为考虑的是补码形式,因此符号位就不能有特殊的意义,需要使用无符号右移
>>>,左边填 0 - 全部转化完后num == 0,所以通过判断最终是否为0,判断有没有转化完
- 使用StringBuilder直接进行字符串拼接…
class Solution {
public String toHex(int num) {
char[] map = {
'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'a', 'b', 'c', 'd', 'e', 'f'};
if (num == 0) return "0";
StringBuilder sb = new StringBuilder();
//无符号右移最高位补0,全部转化完后num == 0,所以通过判断最终是否为0,判断有没有转化完。
while(num != 0){
sb.append(map[num & 0xf]);
num >>>= 4;
}
return sb.reverse().toString();
}
}
168. Excel表列名称-26进制(简单)
给定一个正整数,返回它在 Excel 表中相对应的列名称。
1 -> A
2 -> B
3 -> C
...
26 -> Z
27 -> AA
28 -> AB
...
输入: 28
输出: "AB"
输入: 701
输出: "ZY"
解题思路:这道题的关键在于对 0 的处理,因为26进制范围为[0, 25],但是题目中[A, Z]对应的是[1, 26],因此需要对 n 执行 -1 操作。这样我们可以对n进行26进制转换,然后得到的每一位 + ‘A’并转换为字符进行字符串拼接即可,与前两道题思路是一致的。
class Solution {
public String convertToTitle(int columnNumber) {
if(columnNumber <= 0) return "";
StringBuilder sb = new StringBuilder();
while(columnNumber > 0){
columnNumber--;//这一步是重点!!
sb.append((char)(columnNumber % 26 + 'A'));
columnNumber /= 26;
}
return sb.reverse().toString();
}
}
171. Excel表列序号(简单)
给定一个Excel表格中的列名称,返回其相应的列序号。(与上道题正好相反)
A -> 1
B -> 2
C -> 3
...
Z -> 26
AA -> 27
AB -> 28
...
输入: "AB"
输出: 28
class Solution {
public int titleToNumber(String columnTitle) {
int ans = 0;
char[] c = columnTitle.toCharArray();
for(int i = 0; i < c.length; i++){
//注意这里的加1
ans = ans*26 + (c[i] - 'A' + 1);
}
return ans;
}
}
阶乘
172. 统计阶乘尾部有多少个 0(简单)
给定一个整数 n,返回 n! 结果尾数中零的数量。
输入: 3
输出: 0
解释: 3! = 6, 尾数中没有零。
输入: 5
输出: 1
解释: 5! = 120, 尾数中有 1 个零.
首先,两个数相乘结果末尾有 0,一定是因为两个数中有因子 2 和 5,因为 10 = 2 x 5。也就是说,问题转化为:n!最多可以分解出多少个因子 2 和 5?
比如说n = 25,那么25!最多可以分解出几个 2 和 5 相乘?这个主要取决于能分解出几个因子 5,因为每个偶数都能分解出因子 2,因子 2 肯定比因子 5 多得多。
25!中 5 可以提供一个,10 可以提供一个,15 可以提供一个,20 可以提供一个,25 可以提供两个,总共有 6 个因子 5,所以25!的结果末尾就有 6 个 0。
现在,问题转化为:n!最多可以分解出多少个因子 5?
难点在于像 25,50,125 这样的数,可以提供不止一个因子 5,怎么才能不漏掉呢?
这样,我们假设n = 125,来算一算125!的结果末尾有几个 0:
首先,125 / 5 = 25,这一步就是计算有多少个像 5,15,20,25 这些 5 的倍数,它们一定可以提供一个因子 5。
但是,这些足够吗?刚才说了,像 25,50,75 这些 25 的倍数,可以提供两个因子 5,那么我们再计算出125!中有 125 / 25 = 5 个 25 的倍数,它们每人可以额外再提供一个因子 5。
够了吗?我们发现 125 = 5 x 5 x 5,像 125,250 这些 125 的倍数,可以提供 3 个因子 5,那么我们还得再计算出125!中有 125 / 125 = 1 个 125 的倍数,它还可以额外再提供一个因子 5。
这下应该够了,125!最多可以分解出 25 + 5 + 1 = 31 个因子 5,也就是说阶乘结果的末尾有 31 个 0。
结论:**对于一个数 N,它所包含 5 的个数为:N/5 + N/5^2 + N/5^3 + …,**其中 N/5 表示不大于 N 的数中 5 的倍数贡献一个 5,N/5^2 表示不大于 N 的数中 5^2 的倍数再贡献一个 5 …。
class Solution {
public int trailingZeroes(int n) {
int count = 0;
while(n > 0) {
count += n / 5;
n /= 5;
}
return count;
}
}
如果统计的是 N! 的二进制表示中最低位 1 的位置,只要统计有多少个 2 即可。和求解有多少个 5 一样,2 的个数为 N/2 + N/2^2 + N/2^3 + …
793. 阶乘函数后K个零(困难)
f(x) 是 x! 末尾是 0 的数量。(回想一下 x! = 1 * 2 * 3 * ... * x,且 0! = 1 )
例如, f(3) = 0 ,因3! = 6 的末尾没有 0 ;而 f(11) = 2 ,因为 11!= 39916800 末端有 2 个 0 。给定 K,找出多少个非负整数 x ,能满足 f(x) = K 。
输入:K = 0
输出:5
解释:0!, 1!, 2!, 3!, and 4! 均符合 K = 0 的条件。
输入:K = 5
输出:0
解释:没有匹配到这样的 x!,符合 K = 5 的条件。
一个直观地暴力解法就是穷举呗,因为随着x的增加,x!肯定是递增的,trailingZeroes(x!)肯定也是递增的,伪码逻辑如下:
int res = 0;
for (int x = 0; x < +inf; x++) {
if (trailingZeroes(x) < K) {
continue;
}
if (trailingZeroes(x) > K) {
break;
}
if (trailingZeroes(x) == K) {
res++;
}
}
return res;
前文二分搜索算法说过,对于这种具有单调性的函数,用 for 循环遍历,可以用二分查找进行降维打击,搜索有多少个x满足trailingZeroes(x) == K,其实就是在问,满足条件的x最小是多少,最大是多少,最大值和最小值一减,就可以算出来有多少个x满足条件了。
上一题分析过,x! 末尾有多少个0取决于x!最多可以分解出多少个因子 5。显然,x 每+5,阶乘就会至少多乘一个5,末尾就会至少多一个0,所以如果上面的x有解,那就是5个,如果无解就是0
重点就是二分查找区间的上下界的确定。x的下界我们可以取0;对于上界,由于x 每+5,末尾就会至少多一个0,因而当末尾存在K个0时,x 最大为5*K,因而上边界可以取5*K+1。
注意为了避免整型溢出的问题,需要把所有数据类型改成 long:
class Solution {
public int preimageSizeFZF(long k) {
//注意这里的k改为long
long left = 0, right = 5 * k + 1;
while(left < right){
long mid = left + (right - left)/2;
if(count(mid) < k){
left = mid + 1;
}else if(count(mid) > k){
right = mid;
}else{
return 5;//如果k有解则一定等于5;
}
}
return 0;//无解就是0
}
//求解n!末尾0的个数
private int count(long n){
int sum = 0;
while(n > 0){
sum += n / 5;
n /= 5;
}
return sum;
}
}
字符串加法减法
67. 二进制求和(简单)
给你两个二进制字符串,返回它们的和(用二进制表示)。输入为 非空 字符串且只包含数字 1 和 0
输入: a = "11", b = "1"
输出: "100"
输入: a = "1010", b = "1011"
输出: "10101"
解题思路:先采用最简单的思路实现一下:
class Solution {
public String addBinary(String a, String b) {
int i = a.length() - 1, j = b.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(i >= 0 && j >= 0){
int sum = a.charAt(i) - '0' + b.charAt(j) - '0';
sb.append((carry + sum) % 2);
carry = (sum + carry) / 2;
i--;
j--;
}
while(i >= 0){
int ai = a.charAt(i) - '0';
sb.append((ai + carry) % 2);
carry = (ai + carry) / 2;
i--;
}
while(j >= 0){
int bi = b.charAt(j) - '0';
sb.append((bi + carry) % 2);
carry = (bi+ carry) / 2;
j--;
}
if(carry == 1) sb.append(1);
return sb.reverse().toString();
}
}
简化版本:
class Solution {
public String addBinary(String a, String b) {
StringBuilder ans = new StringBuilder(); //答案
int i = a.length() - 1, j = b.length() - 1; //从最后开始遍历(个位)
int carry = 0; //进位
while(i >= 0 || j >= 0 || carry != 0) {
//如果没有遍历完两个数,或者还有进位
if(i >= 0) carry += a.charAt(i--) - '0'; //如果a还有数
if(j >= 0) carry += b.charAt(j--) - '0'; //如果b还有数
ans.append(carry % 2); //加入当前位的和取模
carry /= 2; //进位
}
return ans.reverse().toString(); //由于计算之后是个位在第一位,所以要反转
}
}
415. 字符串相加(简单)
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和。
解题思路:和上道题思路一致,只是这道题是十进制的加法,只要把对2的除和取余操作变成10就可以了!
class Solution {
public String addStrings(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(carry != 0 || i >= 0 || j >= 0){
if(i >= 0) carry += num1.charAt(i--) - '0';
if(j >= 0) carry += num2.charAt(j--) - '0';
sb.append(carry % 10);
carry /= 10;
}
return sb.reverse().toString();
}
}
43. 字符串相乘(中等)
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
输入: num1 = "2", num2 = "3"
输出: "6"
输入: num1 = "123", num2 = "456"
输出: "56088"
如果 num1和 num2之一是 0,则直接将 0 作为结果返回即可。
如果num1和 num2都不是 0,则可以通过模拟「竖式乘法」的方法计算乘积。从右往左遍历乘数,将乘数的每一位与被乘数相乘得到对应的结果,再将每次得到的结果累加。这道题中,被乘数是num1,乘数是num2。
需要注意的是,num2 除了最低位以外,其余的每一位的运算结果都需要补 0。
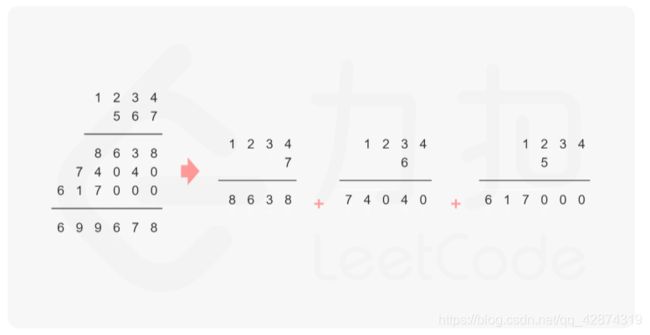
对每次得到的结果进行累加,可以使用「415. 字符串相加」的做法。
class Solution {
public String multiply(String num1, String num2) {
if(num1.equals("0") || num2.equals("0")){
return "0";
}
String ans = "";
// num2 逐位与 num1 相乘
for(int i = num2.length() - 1; i >= 0; i--){
// 保存 num2 第i位数字与 num1 相乘的结果
StringBuilder subSum = new StringBuilder();
// 先根据i的对应位置,在结果补对应个数的0
for (int k = num2.length() - 1; k > i; k--) {
subSum.append(0);
}
// num2 的第 i 位数字 与 num1 相乘的过程
int carry = 0;
for(int j = num1.length() - 1; j >= 0 || carry != 0; j--){
int a = j >= 0 ? num1.charAt(j) - '0' : 0;
int b = num2.charAt(i) - '0';
subSum.append((a * b + carry) % 10);
carry = (a * b + carry)/10;
}
// 将当前结果与新计算的结果求和作为新的结果
ans = addStrings(ans, subSum.reverse().toString());
}
return ans;
}
// 对两个字符串数字进行相加,返回字符串形式的和
public String addStrings(String num1, String num2) {
int i = num1.length() - 1, j = num2.length() - 1;
StringBuilder sb = new StringBuilder();
int carry = 0;
while(carry != 0 || i >= 0 || j >= 0){
if(i >= 0) carry += num1.charAt(i--) - '0';
if(j >= 0) carry += num2.charAt(j--) - '0';
sb.append(carry % 10);
carry /= 10;
}
return sb.reverse().toString();
}
}
相遇问题
453. 最少移动次数使数组元素相等 (简单)
给定一个长度为 n 的 非空 整数数组,每次操作将会使 n - 1 个元素增加 1。找出让数组所有元素相等的最小操作次数。
输入:[1,2,3]
输出:3
解释:只需要3次操作(注意每次操作会增加两个元素的值):
[1,2,3] => [2,3,3] => [3,4,3] => [4,4,4]
解题思路:题目中说的每次操作将会使 n - 1 个元素增加 1,可以联想到,这其实就是每次将一个元素减1。那么为了让每个元素相等,最后必然会减到最小的那个元素的值。所以只需要计算出每个元素减到最小元素的值的次数,再求和就是最终答案
public int minMoves(int[] nums) {
int min = nums[0];
for(int num : nums){
if(num < min){
min = num;
}
}
int move = 0;
for(int num : nums){
move += num - min;
}
return move;
}
462. 最少移动次数使数组元素相等 II(中等)
给定一个非空整数数组,找到使所有数组元素相等所需的最小移动数,其中每次移动可将选定的一个元素加1或减1。 您可以假设数组的长度最多为10000。
输入:[1,2,3]
输出:2
说明:只有两个动作是必要的(记得每一步仅可使其中一个元素加1或减1):
[1,2,3] => [2,2,3] => [2,2,2]
解题思路:这是一个经典的数学问题,当 x 为这个 N 个数的中位数时,可以使得距离最小。具体地,若 N 为奇数,则 x 必须为这 N 个数中的唯一中位数;若 N 为偶数,中间的两个数为 p 和 q,中位数为 (p + q) / 2,此时 x 只要是区间 [p, q] 中的任意一个数即可。
因此,我们只需要找到这个 N 个数的中位数,并计算距离之和。我们可以直接将数组进行排序,这样就直接得到了中位数。
class Solution {
public int minMoves2(int[] nums) {
Arrays.sort(nums);
int mid = nums.length/2;
int move = 0;
for(int num : nums){
move += Math.abs(num - nums[mid]);
}
return move;
}
}
多数投票问题
169. 多数元素(简单)
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
输入:[3,2,3]
输出:3
输入:[2,2,1,1,1,2,2]
输出:2
解题思路:
方法一:哈希表:遍历整个数组,使用哈希映射(HashMap)来存储每个元素以及出现的次数。(其中key为数值,value为出现次数);接着遍历HashMap中的每个Entry,寻找value值 > nums.length / 2 的 key 即可。
class Solution {
public int majorityElement(int[] nums) {
Map<Integer, Integer> map = new HashMap<>();
for(int num : nums){
map.put(num, map.getOrDefault(num, 0) + 1);
if(map.get(num) > nums.length/2){
return num;
}
}
return -1;
}
}
方法二:排序:既然数组中有出现次数> ⌊ n/2 ⌋的元素,那排好序之后的数组中,相同元素总是相邻的。即存在长度> ⌊ n/2 ⌋的一长串 由相同元素构成的连续子数组。那么下标为 n/2的元素(下标从 0 开始)一定是众数。时间复杂度:O(nlog*n)*
class Solution {
public int majorityElement(int[] nums) {
Arrays.sort(nums);
return nums[nums.length / 2];
}
}
下面的图中解释了为什么这种策略是有效的。在下图中,第一个例子是 n 为奇数的情况,第二个例子是 n 为偶数的情况。
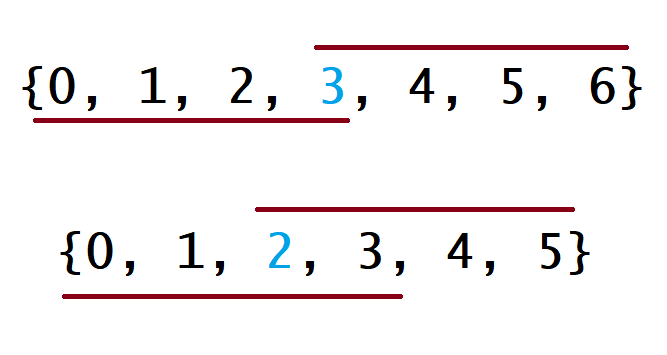
方法三:Boyer-Moore 投票算法
Boyer-Moore 算法的本质和分治十分类似。我们首先给出 Boyer-Moore 算法的详细步骤:
我们维护一个候选众数 candidate 和它出现的次数 count。初始时 candidate 可以为任意值,例如nums[0],count 为 0;
我们遍历数组 nums 中的所有元素,对于每个元素 x,在判断 x 之前,如果 count 的值为 0,我们先将 x 的值赋予 candidate(更换候选人),随后我们判断 x:
-
如果 x 与 candidate 相等,那么计数器 count 的值增加 1;
-
如果 x 与 candidate 不等,那么计数器 count 的值减少 1。
在遍历完成后,candidate 即为整个数组的众数。
为何这行得通呢?
投票法是遇到相同的则票数 + 1,遇到不同的则票数 - 1。且“多数元素”的个数> ⌊ n/2 ⌋,其余元素的个数总和<= ⌊ n/2 ⌋。因此“多数元素”的个数 - 其余元素的个数总和 的结果 肯定 >= 1。这就相当于每个“多数元素”和其他元素 两两相互抵消,抵消到最后肯定还剩余至少1个“多数元素”。
class Solution {
public int majorityElement(int[] nums) {
int candidate = nums[0], count = 0;
for(int num : nums){
if(count == 0) candidate = num;//如果count为0则更换候选人
if(num == candidate){
count++;
}else{
count--;
}
}
return candidate;
}
}
229. 求众数 ll(中等)
给定一个大小为 n 的整数数组,找出其中所有出现超过 ⌊ n/3 ⌋ 次的元素。
**进阶:**尝试设计时间复杂度为 O(n)、空间复杂度为 O(1)的算法解决此问题。
输入:[3,2,3]
输出:[3]
输入:[1,1,1,3,3,2,2,2]
输出:[1,2]
解题思路:和169题的投票算法类似,但是169题是找一个众数,那就只要一个候选,他是保证一定有一个是众数的,直接投票就好但是这个题没有保证有一个元素一定出现 n/3以上。
首先我们得明确,n/k的众数最多只有k-1个,为什么呢?假设有k个众数,n/k * k=n, 这k个元素都是众数,还要不同,怎么可能啊。那么对于这个题,超过n/3的数最多只能有3-1 = 2 个,我们可以先选出两个候选人A,B。 遍历数组,分三种情况:
- 候选1:> n/3
- 候选2:> n/3
- 其他:< n/3
写代码三步走
1、如果投A(当前元素等于A),则A的票数++;
2、如果投B(当前元素等于B),B的票数++;
3、如果A,B都不投(即当前与A,B都不相等),那么检查此时A或B的票数是否为0,如果为0,则当前元素成为新的候选人;如果A,B两个人的票数都不为0,那么A,B两个候选人的票数均减一。
最后会有这么几种可能:有2个大于n/3,有1个大于n/3,有0个大于n/3。遍历结束后选出了两个候选人,但是这两个候选人是否满足>n/3,还需要再遍历一遍数组,找出两个候选人的具体票数,因为题目没有像169题保证一定有。
class Solution {
public List<Integer> majorityElement(int[] nums) {
List<Integer> res = new ArrayList<>();
if (nums == null || nums.length == 0) {
return res;
}
// 定义两个候选者和它们的票数
int cand1 = 0,cand2 = 0;
int cnt1 = 0, cnt2 = 0;
// 投票过程
for (int num : nums) {
// 如果是候选者1,票数++
if (num == cand1) {
cnt1++;
// 一遍遍历,如果你不想写continue,你写多个else if也可以
continue;
}
// 如果是候选者2,票数++
if (num == cand2) {
cnt2++;
continue;
}
// 既不是cand1也不是cand2,如果cnt1为0,那它就去做cand1
if (cnt1 == 0) {
cand1 = num;
cnt1++;
continue;
}
// 如果cand1的数量不为0但是cand2的数量为0,那他就去做cand2
if (cnt2 == 0) {
cand2 = num;
cnt2++;
continue;
}
// 如果cand1和cand2的数量都不为0,那就都-1
cnt1--;
cnt2--;
}
// 检查两个票数符不符合
cnt1 = cnt2 = 0;
for (int num : nums) {
if (num == cand1) {
cnt1++;
} else if (num == cand2) {
// 这里一定要用else if
// 因为可能出现[0,0,0]这种用例,导致两个cand是一样的,写两个if结果就变为[0,0]了
cnt2++;
}
}
if (cnt1 > nums.length / 3) res.add(cand1);
if (cnt2 > nums.length / 3) res.add(cand2);
return res;
}
}
其他
367. 有效的完全平方数(简单)
给定一个 正整数 num ,编写一个函数,如果 num 是一个完全平方数,则返回 true ,否则返回 false 。
进阶:不要 使用任何内置的库函数,如 sqrt 。
解题思路:
方法一:二分查找
class Solution {
public boolean isPerfectSquare(int num) {
int left = 1, right = num;
while(left <= right){
int mid = left + (right - left)/2;
int target = num / mid; //根据target查找会比直接根据平方来比较时间复杂度小很多
if(mid < target){
left = mid + 1;
}else if(mid > target){
right = mid -1;
}else{
//注意这里!当mid = num / mid且num % mid == 0时说明mid为平方根
if(num % mid == 0) return true;
left = mid + 1;
}
}
return false;
}
}
方法二:等差数列
平方序列:1,4,9,16,… 间隔:3,5,7,…
间隔为等差数列,使用这个特性可以得到从 1 开始的平方序列。
class Solution {
public boolean isPerfectSquare(int num) {
int subNum = 1;
while (num > 0) {
num -= subNum;
subNum += 2;
}
return num == 0;
}
}
326. 3的幂(简单)
给定一个整数,写一个函数来判断它是否是 3 的幂次方。如果是,返回 true ;否则,返回 false 。
整数 n 是 3 的幂次方需满足:存在整数 x 使得 n == 3x
输入:n = 27
输出:true
输入:n = 0
输出:false
class Solution {
public boolean isPowerOfThree(int n) {
if (n < 1) {
return false;
}
while (n % 3 == 0) {
n /= 3;
}
return n == 1;
}
}
628. 三个数的最大乘积(简单)
给你一个整型数组 nums ,在数组中找出由三个数组成的最大乘积,并输出这个乘积。
输入:nums = [1,2,3]
输出:6
输入:nums = [-1,-2,-3]
输出:-6
解题思路:
其实全正数和全负数都一样,都是取最大的三个的乘积。 因为三个负数结果肯定是负的,所以要绝对值小的负数,所以还是取最大的3个负数。
第二种情况是有正有负。 假如大部分都是正数,只有一个负数,那还是三个最大的数相乘; 假如负数不止一个,那么可能是两个最小的负数相乘后,负负得正,得到一个很大的数,再乘以最大的正数。 也可能是负数的绝对值很小,而正数的绝对值很大,这个时候还是三个最大的数相乘。
综上所述,总共只有两种结果,最大的三个数相乘,或者两个最小值和最大值相乘。
方法一:排序
class Solution {
public int maximumProduct(int[] nums) {
Arrays.sort(nums);
int n = nums.length;
return Math.max(nums[0] * nums[1] * nums[n - 1], nums[n - 3] * nums[n - 2] * nums[n - 1]);
}
}
我们实际上只要求出数组中最大的三个数以及最小的两个数,因此我们可以不用排序,用线性扫描直接得出这五个数。
class Solution {
public int maximumProduct(int[] nums) {
int max1 = Integer.MIN_VALUE, max2 = Integer.MIN_VALUE, max3 = Integer.MIN_VALUE;
int min1 = Integer.MAX_VALUE, min2 = Integer.MAX_VALUE;
for(int num : nums){
if(num > max1){
max3 = max2;
max2 = max1;
max1 = num;
}else if(num > max2){
max3 = max2;
max2 = num;
}else if(num > max3){
max3 = num;
}
if(num < min1){
min2 = min1;
min1 = num;
}else if(num < min2){
min2 = num;
}
}
return Math.max(max1*max2*max3, min1*min2*max1);
}
}
238. 除自身以外数组的乘积(中等)
给你一个长度为 n 的整数数组 nums,其中 n > 1,返回输出数组 output ,其中 output[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积。
输入: [1,2,3,4]
输出: [24,12,8,6]
说明: 请**不要使用除法,**且在 O(n) 时间复杂度内完成此题。
解题思路:我们不必将所有数字的乘积除以给定索引处的数字得到相应的答案,而是利用索引左侧所有数字的乘积和右侧所有数字的乘积(即前缀与后缀)相乘得到答案。
对于给定索引 i,我们将使用它左边所有数字的乘积乘以右边所有数字的乘积。下面让我们更加具体的描述这个算法。
算法:
- 初始化两个空数组 L 和 R。对于给定索引 i,L[i] 代表的是 i 左侧所有数字的乘积,R[i] 代表的是 i 右侧所有数字的乘积。
- 我们需要用两个循环来填充 L 和 R 数组的值。对于数组 L,L[0] 应该是 1,因为第一个元素的左边没有元素。对于其他元素:L[i] = L[i-1] * nums[i-1]。
- 同理,对于数组 R,R[length-1] 应为 1。length 指的是输入数组的大小。其他元素:R[i] = R[i+1] * nums[i+1]。
- 当 R 和 L 数组填充完成,我们只需要在输入数组上迭代,且索引 i 处的值为:L[i] * R[i]。
class Solution {
public int[] productExceptSelf(int[] nums) {
int length = nums.length;
// L 和 R 分别表示左右两侧的乘积列表
int[] L = new int[length];
int[] R = new int[length];
int[] answer = new int[length];
// L[i] 为索引 i 左侧所有元素的乘积
// 对于索引为 '0' 的元素,因为左侧没有元素,所以 L[0] = 1
L[0] = 1;
for (int i = 1; i < length; i++) {
L[i] = nums[i - 1] * L[i - 1];
}
// R[i] 为索引 i 右侧所有元素的乘积
// 对于索引为 'length-1' 的元素,因为右侧没有元素,所以 R[length-1] = 1
R[length - 1] = 1;
for (int i = length - 2; i >= 0; i--) {
R[i] = nums[i + 1] * R[i + 1];
}
// 对于索引 i,除 nums[i] 之外其余各元素的乘积就是左侧所有元素的乘积乘以右侧所有元素的乘积
for (int i = 0; i < length; i++) {
answer[i] = L[i] * R[i];
}
return answer;
}
}