使用梯度下降法实现变量之间的线性回归
1、介绍
1、概述
本博客的梯度下降法实现变量之间的线性回归,主要考虑到了最小二乘法 X T X X^TX XTX有可能逆不存在的情况。使用该方法求解线性回归的过程如下:

m表示样本的个数,在目标函数前面的系数 1 m \frac{1}{m} m1加不加无所谓,只是为了更好的计算而已,本文的代码中并没有该系数。
2、代码功能
本博客使用梯度下降法来实现对于波士顿平均房价的预测。通过前面的特征矩阵来实现对于波士顿平均房价(medv)的预测。
由于特征矩阵的每一列数据的数量级相差很大,导致模型生成的权重向量数据很大,我们对特征矩阵和分类标签向量的每一列都进行了标准化,即均值为0,方差为1的正态分布。采用的公式如下:
若 X − N ( μ , σ 2 ) , 则 Y = X − μ σ − N ( 0 , 1 ) 若X - N(\mu,\sigma^2),则Y=\frac{X-\mu}{\sigma} - N(0,1) 若X−N(μ,σ2),则Y=σX−μ−N(0,1)
2、代码
1、测试数据boston.csv
(1)数据格式
"id","crim","zn","indus","chas","nox","rm","age","dis","rad","tax","ptratio","black","lstat","medv"
"1",0.00632,18,2.31,0,0.538,6.575,65.2,4.09,1,296,15.3,396.9,4.98,24
"2",0.02731,0,7.07,0,0.469,6.421,78.9,4.9671,2,242,17.8,396.9,9.14,21.6
"3",0.02729,0,7.07,0,0.469,7.185,61.1,4.9671,2,242,17.8,392.83,4.03,34.7
为了大家能够更好的学习最小二乘法,我将这个csv文件放到我博客的资源中,通过下面的链接即可下载,注意在将下面的文件放到代码中运行时,注意修改代码中的文件路径。
https://download.csdn.net/download/weixin_43334389/13134305
3、代码
# @Time : 2020/11/21 20:41
# @Description :
import numpy as np
import pandas as pd
data = pd.read_csv(r"dataset/boston.csv", header=0)
data.drop(["id"], axis=1, inplace=True)
class LinearRegression:
"""
@desc:使用梯度下降回归算法
"""
def __init__(self, learning_rate, times):
"""
@desc:初始化算法
@param learning_rate:学习率。梯度下降步长
@param times:迭代次数
"""
self.learning_rate = learning_rate
self.times = times
def fit(self, X, y):
"""
@desc:训练模型,对样本进行预测
@param X:特征矩阵
@param y:标签数组
"""
# X.shape (400, 14)
# y.shape (400,)
X = np.asarray(X)
y = np.asarray(y)
# 创建权重,初始值为0(也可以试试其他值),长度比X特征数多1,多出的就是w0(截距b)
self.w_ = np.zeros(1 + X.shape[1]) # X.shape[1] 为特征数
# 创建损失值列表,用来每次迭代的损失值。
# 损失值计算公式:(1/2 )*( 预测值 - 真实值)^2
self.loss_ = []
# 开始迭代
for x in range(self.times):
# 为什么使用 self.w_[1:] ? 因为X特征个数比w少1个,所以这里w0先去掉,点乘后再加上
# 矩阵可以使用*运算,但是这里是ndarray数组只能用点乘,1表示x0
y_hat = np.dot(X, self.w_[1:]) + self.w_[0]
# 计算误差
error = y - y_hat
# 将损失值加入损失列表
self.loss_.append(np.sum(error ** 2) / 2)
# 根据差距调整权重w_
# 调整为 w(j)=w(j)+learn_rate*sum((y - y_hat)*x(j))
# 更新w0,将数据x的首项看成1,然后进行更新
self.w_[0] += self.learning_rate * np.sum(error * 1)
# 使用x1到xn的某一列向量(即某一特征)的转置来更新w,也就是将w向x进拟合
# (X.T).shape (14, 400)
# error.shape (400,)
self.w_[1:] += self.learning_rate * np.dot(X.T, error)
def predict(self, X):
"""
@desc:预测测试集数据
@param X:传入的训练集数据
@return:预测结果
"""
X = np.asarray(X)
result = np.dot(X, self.w_[1:]) + self.w_[0]
return result
class StandardScaler:
"""
@desc:对数据集进行标准化处理
"""
def fit(self, X):
"""
@desc:根据传递的样本,计算每个特征列的均值和标准差。在transform()中进行使用,
使得最后返回的均值为0,标准差为1。将每一列变成标准正态分布的形式。
@param X:训练数据。用来计算均值和标准差。
"""
X = np.asarray(X)
self.std_ = np.std(X, axis=0) # 按列计算标准差
self.mean_ = np.mean(X, axis=0) # 按列计算均值
def transform(self, X):
"""
@desc:对给定数据进行标准化处理,将每一列都转换成标准正态分布的形式。
即满足均值为0,标准差为1。
标准化也叫标准差标准化,经过处理的数据符合标准正态分布。
@param X:类数组类型。待转换的训练数据。
@return:返回每一列都是标准正态分布的一个二维数据
"""
return (X - self.mean_) / self.std_
def fit_transform(self, X):
"""
@desc:集fit和transform函数于一体,在训练的时候进行转换操作。
@param X:类数组类型。待转换的训练数据。
@return:返回每一列都是标准正态分布的一个二维数据
"""
self.fit(X)
return self.transform(X)
# 原始梯度下降法的线性回归算法
lr = LinearRegression(learning_rate=0.0005, times=20)
t = data.sample(len(data), random_state=0)
train_X = t.iloc[:400, :-1]
train_y = t.iloc[:400, -1]
test_X = t.iloc[400:, :-1]
test_y = t.iloc[400:, -1]
lr.fit(train_X, train_y)
result = lr.predict(test_X)
print("--------标准化之前的训练和预测的损失值和权重------------------")
print(np.mean((result - test_y) ** 2))
print(lr.w_)
print(lr.loss_)
# 标准化之后的梯度下降法的线性回归算法
# 为了避免每个特征数量级的不同对梯度下降造成的影响。我们对每个特征进行标准化。
# 将每个特征列排除数量级的影响,将其变成同样的一个数量级。
lr = LinearRegression(learning_rate=0.0005, times=20)
# data.shape (506, 14)
print("data.shape", data.shape)
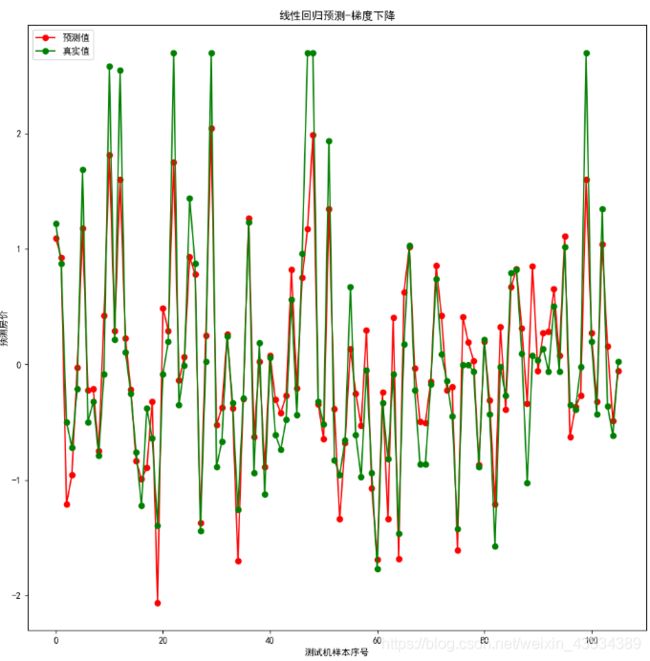
# type(data) (3)权重拟合的曲线和预测绘制的曲线进行对比

(4)标准化数据前后的均方误差、权重和损失值对比
--------标准化之前的训练和预测的损失值和权重------------------
2.5269094172606156e+194
[-4.91840744e+91 -2.24201028e+92 -4.88461060e+92 -5.87006550e+92
-3.32031749e+90 -2.77875440e+91 -3.06624018e+92 -3.47870767e+93
-1.79024405e+92 -5.41134085e+92 -2.15329860e+94 -9.17485507e+92
-1.74958006e+94 -6.49542169e+92]
[116831.44, 352143849427807.9, 1.3577876251262872e+24, 5.238506743432333e+33,...
--------标准化之后的训练和预测的损失值和权重------------------
0.149072143352611
[ 1.49824597e-16 -7.82096101e-02 3.27417218e-02 -4.18423834e-02
7.23915815e-02 -1.22422484e-01 3.18709730e-01 -9.44094559e-03
-2.09320117e-01 1.04023908e-01 -5.20477318e-02 -1.82216410e-01
9.76133507e-02 -3.94395606e-01]
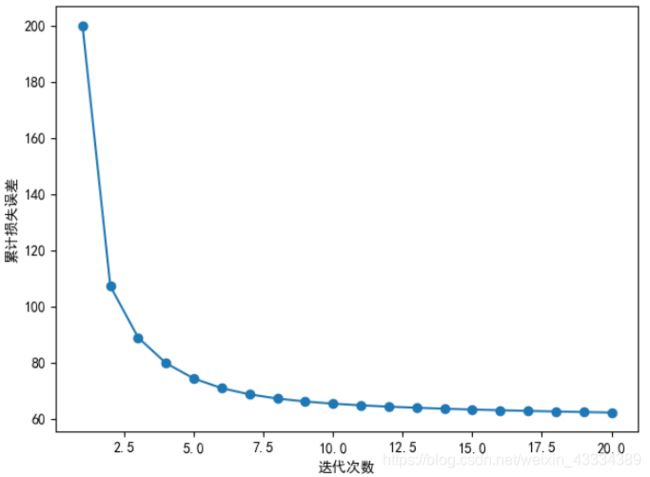
[200.0, 107.18106695239439, 88.90466866295793, 79.78035025519532, 74.3187880885867, 70.90417512718281, 68.69155318506807, 67.20013197881178, 66.15079837015878, 65.37902020765745, 64.78625525603303, 64.31246996531246, 63.920412106879105, 63.586500210988966, 63.295479267264845, 63.03724485771134, 62.80493063951664, 62.5937408804752, 62.40022787877571, 62.221838400632855]
3、分析
1、核心代码分析
# 这里对应梯度下降法求解线性回归的结论。内积也可以表示一种求和
self.w_[1:] += self.learning_rate * np.dot(X.T, error)
# 举例,对应上面的内积内容
error = np.array([1, 2])
print(error)
# 我们的波士顿数据格式如下,这里并没有在该矩阵的前面的添加数字1(为了和增广权向量的首项 w 0 w_0 w0相对应),是因为我们事先知道第一列是数字1,在代码中,为了简便,我们将有数字1的项和其他项分开,单独计算并更新相应权重。在分别训练好权重 s e l f . w [ 1 : ] , s e l f . w [ 0 ] self.w_[1:],self.w_[0] self.w[1:],self.w[0]后,将 w 0 w_0 w0加到函数表达式$ result = np.dot(X, self.w_[1:]) + self.w_[0]$中即可。
通过上文介绍的梯度下降法求解线性回归过程,我们可以看到在结论中,都要乘以一项 x j ( i ) x_j^{(i)} xj(i),而该项正对应下面X矩阵的每一列数据。为了能够和 y − y h a t y - y_{hat} y−yhat相乘后求和,这里刚好对应代码中的 n p . d o t ( X . T , e r r o r ) np.dot(X.T, error) np.dot(X.T,error)。
X = [ x 11 x 12 ⋯ x 1 p x 21 x 22 ⋯ x 2 p ⋯ x n 1 x n 2 ⋯ x n p ] X= \left[ \begin{array}{c} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \cdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{array} \right] X=⎣⎢⎢⎡x11x21⋯xn1x12x22xn2⋯⋯⋯x1px2pxnp⎦⎥⎥⎤
2、由于这里涉及到了NumPy中的ndarray与Pandas的Series和DataFrame中的关系,我在下面这篇博客中进行简单叙述。
https://blog.csdn.net/weixin_43334389/article/details/109962837