三次样条拟合(附完整代码)
文章目录
- 一、推导步骤
- 二、三种不同端点约束下的三次样条拟合
-
- 1、给定起始速度 v 0 v_0 v0与结束速度 v n v_n vn
- 2、起始位置 q 0 q_0 q0与结束位置 q n q_n qn相等(数据需满足的特性,非约束条件),起始速度 v 0 v_0 v0与结束速度 v n v_n vn相等,起始加速度 a 0 a_0 a0与结束加速度 a n a_n an相等(周期三次样条)
- 3、给定起始速度 v 0 v_0 v0、结束速度 v n v_n vn、起始加速度 a 0 a_0 a0、结束加速度 a n a_n an
- 三、给定拟合精度的三次样条拟合
- 四、参考文献
一、推导步骤
给定 n + 1 n+1 n+1个点 ( t i , q i ) , i = 0 , 1 , . . . , n (t_i,q_i),i=0,1,...,n (ti,qi),i=0,1,...,n,求解 n n n段三次多项式 q k ( t ) q_k(t) qk(t),使得拼接而成的三次样条曲线 s ( t ) s(t) s(t)尽可能经过所有给定点(起点与终点通常要求经过),曲线尽可能平滑(曲率或加速度尽可能小),而且二阶连续。三次样条曲线 s ( t ) s(t) s(t)定义如下:
{ s ( t ) = { q k ( t ) , t ∈ [ t k , t k + 1 ] , k = 0 , 1 , . . . , n − 1 } q k ( t ) = a k 0 + a k 1 ( t − t k ) + a k 2 ( t − t k ) 2 + a k 3 ( t − t k ) 3 (1) \begin{cases} s(t) = \{q_k(t),t\in[t_k,t_{k+1}],k=0,1,...,n-1\} \\ q_k(t)=a_{k0}+a_{k1}(t-t_k)+a_{k2}(t-t_k)^2+a_{k3}(t-t_k)^3 \\ \tag 1 \end{cases} { s(t)={ qk(t),t∈[tk,tk+1],k=0,1,...,n−1}qk(t)=ak0+ak1(t−tk)+ak2(t−tk)2+ak3(t−tk)3(1)
求解三次样条的系数则通过最小化以下目标函数:
L = μ ∑ k = 0 n w k ( s ( t k ) − q k ) 2 + ( 1 − μ ) ∫ t 0 t n s ¨ ( t ) 2 d t (2) L = \mu\sum_{k=0}^{n}w_k(s(t_k)-q_k)^2+(1-\mu) \int_{t_0}^{t_n}\ddot s(t)^2dt \tag 2 L=μk=0∑nwk(s(tk)−qk)2+(1−μ)∫t0tns¨(t)2dt(2)
其中,参数 μ ∈ ( 0 , 1 ] \mu\in(0,1] μ∈(0,1],用于衡量两个不同的优化指标(曲线更好地靠近给定点、曲线的平滑性)的重要程度。 w k w_k wk为第 k k k个点的权重,用于调整样条曲线在该点的拟合精度。
式(2)目标函数可以进一步推导得到:
L = ∑ k = 0 n w k ( s ( t k ) − q k ) 2 + λ ∑ k = 0 n − 1 2 T k ( ω k 2 + ω k ω k + 1 + ω k + 1 2 ) (3) L = \sum_{k=0}^{n}w_k(s(t_k)-q_k)^2+ \lambda \sum_{k=0}^{n-1}2T_k(\omega_k^2+\omega_k\omega_{k+1}+\omega_{k+1}^2) \tag 3 L=k=0∑nwk(s(tk)−qk)2+λk=0∑n−12Tk(ωk2+ωkωk+1+ωk+12)(3)
其中, λ = ( 1 − μ ) / ( 6 μ ) \lambda=(1-\mu)/(6\mu) λ=(1−μ)/(6μ)。
式(3)写成:
L = ( q − s ) T W ( q − s ) + λ ω T A ω (4) L = (q-s)^TW(q-s)+\lambda \omega^TA \omega \tag 4 L=(q−s)TW(q−s)+λωTAω(4)
其中, s s s为待优化求解的向量, ω = [ ω 0 , . . . , ω n ] T \omega=[\omega_0,...,\omega_n]^T ω=[ω0,...,ωn]T为给定点处的加速度向量(未知), W = d i a g { w 0 , . . . , w n } W=diag\{ w_0,...,w_n\} W=diag{ w0,...,wn}为对角线为权向量的矩阵, A A A为矩阵,定义为:
A = [ 2 T 0 T 0 0 ⋯ 0 T 0 2 ( T 0 + T 1 ) T 1 0 ⋮ 0 ⋱ 0 ⋮ 0 T n − 2 2 ( T n − 2 + T n − 1 ) T n − 1 0 ⋯ 0 T n − 1 2 T n − 1 ) ] (5) A=\left[ \begin{matrix} 2T_0 & T_0 & 0 & \cdots & 0\\ T_0 & 2(T_0+T_1) & T_1 & 0 & \vdots \\ 0 & & \ddots & & 0 \\ \vdots &0 & T_{n-2} & 2(T_{n-2}+T_{n-1}) & T_{n-1} \\ 0 & \cdots & 0 & T_{n-1} & 2T_{n-1}) \end{matrix} \right] \tag {5} A=⎣⎢⎢⎢⎢⎢⎢⎡2T0T00⋮0T02(T0+T1)0⋯0T1⋱Tn−20⋯02(Tn−2+Tn−1)Tn−10⋮0Tn−12Tn−1)⎦⎥⎥⎥⎥⎥⎥⎤(5)
式(4)包含未知量 s s s与 ω \omega ω,必须找到两者关系,并将其一代换掉。对于 v 0 = 0 , v n = 0 v_0=0,v_n=0 v0=0,vn=0的情况,有关系:
A ω = C s (6) A \omega=Cs \tag 6 Aω=Cs(6)
其中,
C = [ − 6 / T 0 6 / T 0 0 ⋯ 0 6 / T 0 − ( 6 / T 0 + 6 / T 1 ) 6 / T 1 ⋮ 0 6 / T 1 − ( 6 / T 1 + 6 / T 2 ) 6 / T 2 ⋮ ⋱ 0 6 / T n − 2 − ( 6 / T n − 2 + 6 / T n − 1 ) 6 / T n − 1 0 ⋯ 0 6 / T n − 1 − 6 / T n − 1 ) ] (7) C=\left[ \begin{matrix} -6/T_0 & 6/T_0 & 0 & \cdots & 0\\ 6/T_0 & -(6/T_0+6/T_1) & 6/T_1 & & \vdots \\ 0 & 6/T_1 & -(6/T_1+6/T_2) & 6/T_2 & \\ \vdots & & & \ddots & 0 \\ & & 6/T_{n-2} & -(6/T_{n-2}+6/T_{n-1}) & 6/T_{n-1} \\ 0 & \cdots & 0 & 6/T_{n-1} & -6/T_{n-1}) \end{matrix} \right] \tag {7} C=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡−6/T06/T00⋮06/T0−(6/T0+6/T1)6/T1⋯06/T1−(6/T1+6/T2)6/Tn−20⋯6/T2⋱−(6/Tn−2+6/Tn−1)6/Tn−10⋮06/Tn−1−6/Tn−1)⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤(7)
由式(6)得:
ω = A − 1 C s (8) \omega=A^{-1}Cs \tag 8 ω=A−1Cs(8)
上式代入式(4),由于矩阵 A A A为实对称矩阵, ( A T ) − 1 = A − 1 (A^T)^{-1}=A^{-1} (AT)−1=A−1,化简得到:
L ( s ) = ( q − s ) T W ( q − s ) + λ s T C T A − 1 C s (9) L(s) = (q-s)^TW(q-s)+\lambda s^TC^TA^{-1}Cs \tag 9 L(s)=(q−s)TW(q−s)+λsTCTA−1Cs(9)
极值点在一阶导数为0处取得,对式(9)求导并令其为0:
− ( q − s ) T W + λ s T C T A − 1 C = 0 (10) -(q-s)^TW+\lambda s^TC^TA^{-1}C=0 \tag {10} −(q−s)TW+λsTCTA−1C=0(10)
解得:
s = ( W + λ C T A − 1 C ) − 1 W q (11) s =(W+\lambda C^TA^{-1}C)^{-1}Wq \tag {11} s=(W+λCTA−1C)−1Wq(11)
可以看到式(11)需要求逆矩阵两次,利用矩阵求逆引理(matrix inversion lemma),上式可以写成:
s = q − λ W − 1 C T ( A + λ C W − 1 C T ) − 1 C q (12) s =q-\lambda W^{-1}C^T(A+\lambda C W^{-1}C^T)^{-1}Cq \tag {12} s=q−λW−1CT(A+λCW−1CT)−1Cq(12)
由于 W W W为对角阵,很容易求得逆矩阵,因而式(12)只需求解矩阵 A + λ C W − 1 C T A+\lambda C W^{-1}C^T A+λCW−1CT的逆一次。
进一步,可以将式(12)分步进行,求解矩阵方程:
( A + λ C W − 1 C T ) ω = C q (13) (A+\lambda C W^{-1}C^T) \omega =Cq \tag {13} (A+λCW−1CT)ω=Cq(13)
然后代入下式:
s = q − λ W − 1 C T ω (14) s =q-\lambda W^{-1}C^T\omega \tag {14} s=q−λW−1CTω(14)
更一般地,给定的端点条件可能并非 v 0 = 0 v_0=0 v0=0与 v n = 0 v_n=0 vn=0,这时根据式(13)(14)求得的新位置 s s s,修改其端点约束,再利用三次样条进行插值即可(采用新的端点约束后,曲线形状会有一点变化)。参见博文:三次样条插值(附完整代码)。
这里实现了三种不同给定约束的三次样条拟合:
(1) 给定起始速度 v 0 v_0 v0与结束速度 v n v_n vn
(2) 起始位置 q 0 q_0 q0与结束位置 q n q_n qn相等(数据需满足的特性,非约束条件),起始速度 v 0 v_0 v0与结束速度 v n v_n vn相等,起始加速度 a 0 a_0 a0与结束加速度 a n a_n an相等(周期三次样条)
(3) 给定起始速度 v 0 v_0 v0、结束速度 v n v_n vn、起始加速度 a 0 a_0 a0、结束加速度 a n a_n an
当指定拟合精度时,利用二分法可以迭代得到参数 μ \mu μ,再进行以上三种不同给定约束的三次样条拟合。
二、三种不同端点约束下的三次样条拟合
%{
Function: estimate_new_position
Description: 估计新的位置
Input: 系数lambda, 对角矩阵inverseW, 原来位置向量q, 时间间隔向量T, 数据点个数count
Output: 新的位置向量s
Author: Marc Pony(marc_pony@163.com)
%}
function s = estimate_new_position(lambda, inverseW, q, T, count)
a = zeros(count, 1);
b = zeros(count, 1);
c = zeros(count, 1);
for i = 1 : count - 1
a(i + 1) = T(i);
end
b(1) = 2.0 * T(1);
for i = 2 : count - 1
b(i) = 2.0 * (T(i - 1) + T(i));
end
b(count) = 2.0 * T(count - 1);
for i = 1 : count - 1
c(i) = T(i);
end
A = diag(a(2 : count), -1) + diag(b, 0) + diag(c(1 : count - 1), 1);
aa = zeros(count, 1);
bb = zeros(count, 1);
cc = zeros(count, 1);
for i = 1 : count - 1
aa(i + 1) = 6.0 / T(i);
end
bb(1) = -6.0 / T(1);
for i = 2 : count - 1
bb(i) = -(6.0 / T(i - 1) + 6.0 / T(i));
end
bb(count) = -6.0 / T(count - 1);
for i = 1 : count - 1
cc(i) = 6.0 / T(i);
end
C = diag(aa(2 : count), -1) + diag(bb, 0) + diag(cc(1 : count - 1), 1);
omegaTemp = (A + lambda * C * inverseW * C') \ (C * q);
s = q - lambda * inverseW * C' * omegaTemp;
end
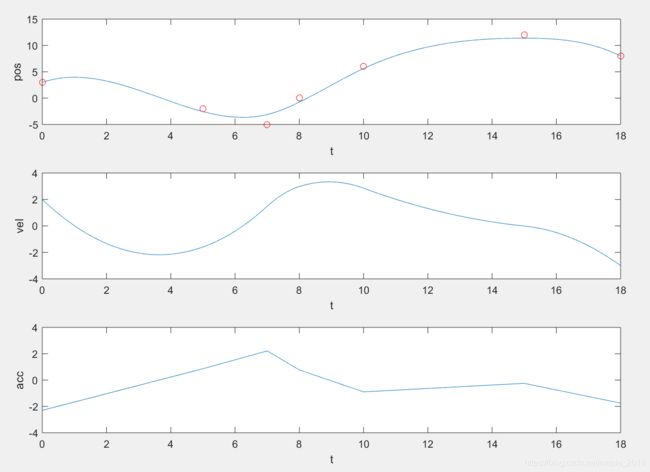
1、给定起始速度 v 0 v_0 v0与结束速度 v n v_n vn
clc;
clear;
close all;
t = [0, 5, 7, 8, 10, 15, 18]'; %递增时间序列
q = [3, -2, -5, 0, 6, 12, 8]';
inverseW = diag([0, 1, 1, 1, 1, 1, 0]); %严格经过起点与终点(值越接近于0,曲线越靠近给定点)
mu = 0.6; %在(0, 1]之间取值,用于衡量两个不同的优化指标(曲线更好地靠近给定点、曲线的平滑性)的重要程度
lambda = (1.0 - mu) / (6.0 * mu);
qNew = estimate_new_position(lambda, inverseW, q, diff(t), length(t));
v0 = 2; %起始速度
vn = -3; %结束速度
deltaT = 0.001; %插补周期
n = length(t); % n >= 4
T = diff(t);
a = zeros(n, 1);
b = zeros(n, 1);
c = zeros(n, 1);
d = zeros(n, 1);
for i = 1 : n - 1
a(i + 1) = T(i);
end
b(1) = 2.0 * T(1);
for i = 2 : n - 1
b(i) = 2.0 * (T(i - 1) + T(i));
end
b(n) = 2.0 * T(n - 1);
for i = 1 : n - 1
c(i) = T(i);
end
d(1) = 6.0 * ((qNew(2) - qNew(1)) / T(1) - v0);
for i = 2 : n - 1
d(i) = 6.0 * ((qNew(i + 1) - qNew(i)) / T(i) - (qNew(i) - qNew(i - 1)) / T(i - 1));
end
d(n) = 6.0 * (vn - (qNew(n) - qNew(n - 1)) / T(n - 1));
[omega, sta] = solve_tridiagonal_matrix_equation(a, b, c, d, n);
if sta == 0
error('三对角矩阵方程求解出错!');
end
time = [];
pos = [];
vel = [];
acc = [];
time = [time; t(1)];
pos = [pos; qNew(1)];
vel = [vel; v0];
acc = [acc; omega(1)];
for i = 1 : n - 1
tt = (t(i) + deltaT : deltaT : t(i + 1))';
a0 = qNew(i);
a1 = (qNew(i + 1) - qNew(i)) / T(i) - T(i) * (omega(i + 1) + 2.0 * omega(i)) / 6.0;
a2 = 0.5 * omega(i);
a3 = (omega(i + 1) - omega(i)) / (6.0 * T(i));
time = [time; tt];
pos = [pos; a0 + (tt - t(i)) .* (a1 + (tt - t(i)) .* (a2 + a3 .* (tt - t(i))))];
vel = [vel; a1 + (tt - t(i)) .* (2.0 * a2 + 3.0 * a3 .* (tt - t(i)))];
acc = [acc; 2.0 * a2 + 6.0 * a3 .* (tt - t(i))];
end
if abs(time(end) - t(n)) > 1.0e-8
time = [time; t(n)];
pos = [pos; qNew(n)];
vel = [vel; vn];
acc = [acc; omega(n)];
end
figure(1)
subplot(3, 1, 1)
plot(time, pos);
hold on
plot(t, q, 'ro');
xlabel('t')
ylabel('pos')
subplot(3, 1, 2)
plot(time, vel);
xlabel('t')
ylabel('vel')
subplot(3, 1, 3)
plot(time, acc);
xlabel('t')
ylabel('acc')
2、起始位置 q 0 q_0 q0与结束位置 q n q_n qn相等(数据需满足的特性,非约束条件),起始速度 v 0 v_0 v0与结束速度 v n v_n vn相等,起始加速度 a 0 a_0 a0与结束加速度 a n a_n an相等(周期三次样条)
clc;
clear;
close all;
t = [0, 5, 7, 8, 10, 15, 18]'; %递增时间序列
q = [3, -2, -5, 0, 6, 12, 3]'; %首尾数据一致
deltaT = 0.001; %插补周期
forwardPeriodCount = 2;
backwardPeriodCount = 1;
inverseW = diag([0, 1, 1, 1, 1, 1, 0]); %严格经过起点与终点(值越接近于0,曲线越靠近给定点)
mu = 0.9;%在(0, 1]之间取值,用于衡量两个不同的优化指标(曲线更好地靠近给定点、曲线的平滑性)的重要程度
lambda = (1.0 - mu) / (6.0 * mu);
n = length(t);
T = diff(t);
s = estimate_new_position(lambda, inverseW, q, T, n);
a = zeros(n - 1, 1);
b = zeros(n - 1, 1);
c = zeros(n - 1, 1);
d = zeros(n - 1, 1);
a(1 : n - 1) = T(1 : n - 1);
b(1) = 2.0 * (T(n - 1) + T(1));
for i = 2 : n - 1
b(i) = 2.0 * (T(i - 1) + T(i));
end
c(1) = T(n - 1);
for i = 2 : n - 2
c(i) = T(i - 1);
end
c(n - 1) = T(n - 2);
d(1) = 3.0 * (T(n - 1)^2 * (s(2) - s(1)) + T(1)^2 * (s(n) - s(n - 1))) / (T(n - 1) * T(1));
for i = 2 : n - 1
d(i) = 3.0 * (T(i - 1)^2 * (s(i + 1) - s(i)) + T(i)^2 * (s(i) - s(i - 1))) / (T(i - 1) * T(i));
end
[v, sta] = solve_cyclic_tridiagonal_matrix_equation(a, b, c, d, n - 1);
if sta == 0
error('循环三对角矩阵方程求解出错!');
end
v = [v; v(1)];
time = [];
pos = [];
vel = [];
acc = [];
time = [time; t(1)];
pos = [pos; s(1)];
vel = [vel; v(1)];
acc = [acc; 2.0 * (3.0 * (s(2) - s(1)) / T(1) - 2.0 * v(1) - v(2)) / T(1)];
for i = 1 : n - 1
tt = (t(i) + deltaT : deltaT : t(i + 1))';
a0 = s(i);
a1 = v(i);
a2 = (3.0 * (s(i + 1) - s(i)) / T(i) - 2.0 * v(i) - v(i + 1)) / T(i);
a3 = (2.0 * (s(i) - s(i + 1)) / T(i) + v(i) + v(i + 1)) / T(i)^2;
time = [time; tt];
pos = [pos; a0 + (tt - t(i)) .* (a1 + (tt - t(i)) .* (a2 + a3 .* (tt - t(i))))];
vel = [vel; a1 + (tt - t(i)) .* (2.0 * a2 + 3.0 * a3 .* (tt - t(i)))];
acc = [acc; 2.0 * a2 + 6.0 * a3 .* (tt - t(i))];
end
if abs(time(end) - t(n)) > 1.0e-8
a2 = (3.0 * (s(n) - s(n - 1)) / T(n - 1) - 2.0 * v(n - 1) - v(n)) / T(n - 1);
a3 = (2.0 * (s(n - 1) - s(n)) / T(n - 1) + v(n - 1) + v(n)) / T(n - 1)^2;
time = [time; t(n)];
pos = [pos; s(n)];
vel = [vel; v(n)];
acc = [acc; 2.0 * a2 + 6.0 * a3 .* T(n - 1)];
end
period = time(end) - time(1);
figure(1)
subplot(3, 1, 1)
plot(time, pos, 'k');
hold on
plot(t, q, 'ko');
for i = 1 : forwardPeriodCount
plot(time + i * period, pos, '--');
plot(t + i * period, q, 'bo');
end
for i = 1 : backwardPeriodCount
plot(time - i * period, pos, '--');
plot(t - i * period, q, 'bo');
end
xlabel('t')
ylabel('pos')
subplot(3, 1, 2)
plot(time, vel, 'k');
hold on
for i = 1 : forwardPeriodCount
plot(time + i * period, vel, '--');
end
for i = 1 : backwardPeriodCount
plot(time - i * period, vel, '--');
end
xlabel('t')
ylabel('vel')
subplot(3, 1, 3)
plot(time, acc, 'k');
hold on
for i = 1 : forwardPeriodCount
plot(time + i * period, acc, '--');
end
for i = 1 : backwardPeriodCount
plot(time - i * period, acc, '--');
end
xlabel('t')
ylabel('acc')
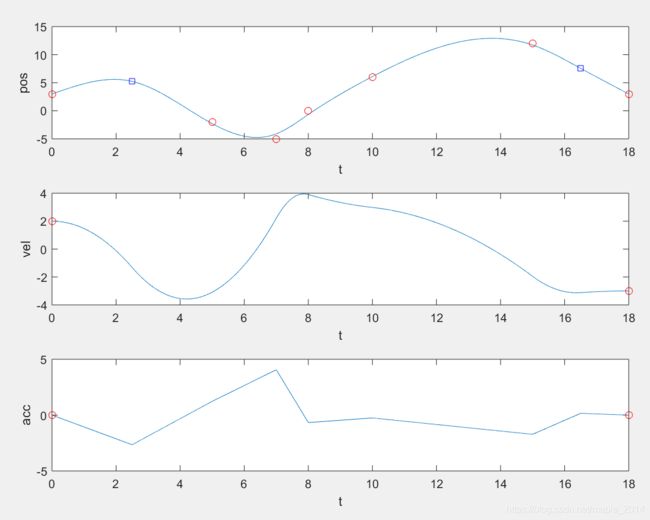
3、给定起始速度 v 0 v_0 v0、结束速度 v n v_n vn、起始加速度 a 0 a_0 a0、结束加速度 a n a_n an
clc;
clear;
close all;
t = [0, 5, 7, 8, 10, 15, 18]'; %递增时间序列
q = [3, -2, -5, 0, 6, 12, 3]';
inverseW = diag([0, 1, 1, 1, 1, 1, 0]); %严格经过起点与终点(值越接近于0,曲线越靠近给定点)
mu = 0.9;%在(0, 1]之间取值,用于衡量两个不同的优化指标(曲线更好地靠近给定点、曲线的平滑性)的重要程度
lambda = (1.0 - mu) / (6.0 * mu);
qNew = estimate_new_position(lambda, inverseW, q, diff(t), length(t));
v0 = 2; %起始速度
vn = -3; %结束速度
a0 = 0; %起始加速度
an = 0; %结束加速度
deltaT = 0.001; %插补周期
%前两个时间之间、后两个时间之间插入时间
n = length(t); % n >= 4
t2 = 0.5 * (t(1) + t(2));
t_n_1 = 0.5 * (t(n) + t(n - 1));
t = [t(1); t2; t(2 : n - 1); t_n_1; t(n)];
qNew = [qNew(1); 0.0; qNew(2 : n - 1); 0.0; qNew(n)];
n = n + 2;
T = diff(t);
a = zeros(n - 2, 1);
b = zeros(n - 2, 1);
c = zeros(n - 2, 1);
d = zeros(n - 2, 1);
a(2) = T(2) - T(1)^2 / T(2);
for i = 3 : n - 2
a(i) = T(i);
end
b(1) = 2.0 * T(2) + T(1) * (3.0 + T(1) / T(2));
for i = 2 : n - 3
b(i) = 2.0 * (T(i) + T(i + 1));
end
b(n - 2) = 2.0 * T(n - 2) + T(n - 1) * (3.0 + T(n - 1) / T(n - 2));
for i = 1 : n - 4
c(i) = T(i + 1);
end
c(n - 3) = T(n - 2) - T(n - 1)^2 / T(n - 2);
d(1) = 6.0 * ((qNew(3) - qNew(1)) / T(2) - v0 * (1.0 + T(1) / T(2)) - a0 * (0.5 + T(1) / (3.0 * T(2))) * T(1));
d(2) = 6.0 * ((qNew(4) - qNew(3)) / T(3) - (qNew(3) - qNew(1)) / T(2) + v0 * T(1) / T(2) + a0 * T(1)^2 / (3.0 * T(2)));
for i = 3 : n - 4
d(i) = 6.0 * ((qNew(i + 2) - qNew(i + 1)) / T(i + 1) - (qNew(i + 1) - qNew(i)) / T(i));
end
d(n - 3) = 6.0 * ((qNew(n) - qNew(n - 2)) / T(n - 2) - (qNew(n - 2) - qNew(n - 3)) / T(n - 3) - vn * T(n - 1) / T(n - 2) + an * T(n - 1)^2 / (3.0 * T(n - 2)));
d(n - 2) = 6.0 * ((qNew(n - 2) - qNew(n)) / T(n - 2) + vn * (1.0 + T(n - 1) / T(n - 2)) - an * (0.5 + T(n - 1) / (3.0 * T(n - 2))) * T(n - 1));
[w, sta] = solve_tridiagonal_matrix_equation(a, b, c, d, n - 2);
if sta == 0
error('三对角矩阵方程求解出错!');
end
w = [a0; w; an];
qNew(2) = qNew(1) + T(1) * v0 + T(1)^2 * a0 / 3.0 + T(1)^2 * w(2) / 6.0;
qNew(n - 1) = qNew(n) - T(n - 1) * vn + T(n - 1)^2 * an / 3.0 + T(n - 1)^2 * w(n - 1) / 6.0;
time = [];
pos = [];
vel = [];
acc = [];
time = [time; t(1)];
pos = [pos; qNew(1)];
vel = [vel; v0];
acc = [acc; a0];
for i = 1 : n - 1
tt = (t(i) + deltaT : deltaT : t(i + 1))';
b0 = qNew(i);
b1 = (qNew(i + 1) - qNew(i)) / T(i) - T(i) * (w(i + 1) + 2.0 * w(i)) / 6.0;
b2 = 0.5 * w(i);
b3 = (w(i + 1) - w(i)) / (6.0 * T(i));
time = [time; tt];
pos = [pos; b0 + (tt - t(i)) .* (b1 + (tt - t(i)) .* (b2 + b3 .* (tt - t(i))))];
vel = [vel; b1 + (tt - t(i)) .* (2.0 * b2 + 3.0 * b3 .* (tt - t(i)))];
acc = [acc; 2.0 * b2 + 6.0 * b3 .* (tt - t(i))];
end
if abs(time(end) - t(n)) > 1.0e-8
time = [time; t(n)];
pos = [pos; qNew(n)];
vel = [vel; vn];
acc = [acc; an];
end
figure(1)
subplot(3, 1, 1)
plot(time, pos);
hold on
plot(t([1, 3 : n - 2, n]), q, 'ro');
plot(t([2, n - 1]), qNew([2, n - 1]), 'bs');
xlabel('t')
ylabel('pos')
subplot(3, 1, 2)
plot(time, vel);
hold on
plot(t([1, n]), [v0, vn], 'ro');
xlabel('t')
ylabel('vel')
subplot(3, 1, 3)
plot(time, acc);
hold on
plot(t([1, n]), [a0, an], 'ro');
xlabel('t')
ylabel('acc')
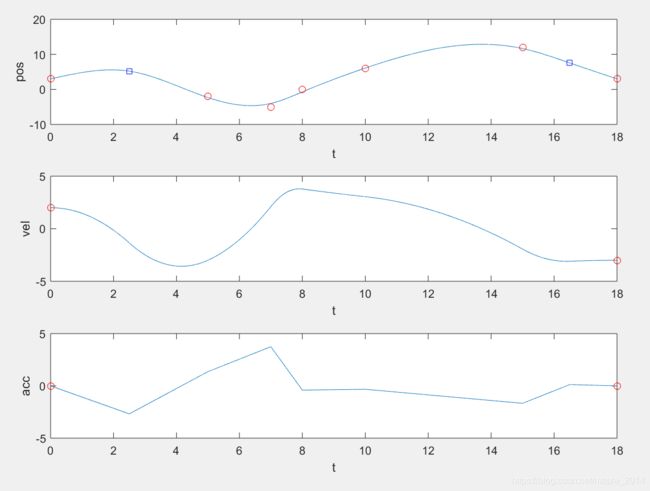
三、给定拟合精度的三次样条拟合
clc;
clear;
close all;
t = [0, 5, 7, 8, 10, 15, 18]'; %递增时间序列
q = [3, -2, -5, 0, 6, 12, 3]';
inverseW = diag([0, 1, 1, 1, 1, 1, 0]); %严格经过起点与终点(值越接近于0,曲线越靠近给定点)
maxEpsilon = 1;
maxIterations = 20;
leftMu = 0.0;
rightMu = 1.0;
for i = 1 : maxIterations
mu = 0.5 * (leftMu + rightMu);
lambda = (1.0 - mu) / (6.0 * mu);
qNew = estimate_new_position(lambda, inverseW, q, diff(t), length(t));
epsilon = max(abs(q - qNew));
if epsilon > maxEpsilon
leftMu = mu;
else
rightMu = mu;
end
end
v0 = 2; %起始速度
vn = -3; %结束速度
a0 = 0; %起始加速度
an = 0; %结束加速度
deltaT = 0.001; %插补周期
%前两个时间之间、后两个时间之间插入时间
n = length(t); % n >= 4
t2 = 0.5 * (t(1) + t(2));
t_n_1 = 0.5 * (t(n) + t(n - 1));
t = [t(1); t2; t(2 : n - 1); t_n_1; t(n)];
qNew = [qNew(1); 0.0; qNew(2 : n - 1); 0.0; qNew(n)];
n = n + 2;
T = diff(t);
a = zeros(n - 2, 1);
b = zeros(n - 2, 1);
c = zeros(n - 2, 1);
d = zeros(n - 2, 1);
a(2) = T(2) - T(1)^2 / T(2);
for i = 3 : n - 2
a(i) = T(i);
end
b(1) = 2.0 * T(2) + T(1) * (3.0 + T(1) / T(2));
for i = 2 : n - 3
b(i) = 2.0 * (T(i) + T(i + 1));
end
b(n - 2) = 2.0 * T(n - 2) + T(n - 1) * (3.0 + T(n - 1) / T(n - 2));
for i = 1 : n - 4
c(i) = T(i + 1);
end
c(n - 3) = T(n - 2) - T(n - 1)^2 / T(n - 2);
d(1) = 6.0 * ((qNew(3) - qNew(1)) / T(2) - v0 * (1.0 + T(1) / T(2)) - a0 * (0.5 + T(1) / (3.0 * T(2))) * T(1));
d(2) = 6.0 * ((qNew(4) - qNew(3)) / T(3) - (qNew(3) - qNew(1)) / T(2) + v0 * T(1) / T(2) + a0 * T(1)^2 / (3.0 * T(2)));
for i = 3 : n - 4
d(i) = 6.0 * ((qNew(i + 2) - qNew(i + 1)) / T(i + 1) - (qNew(i + 1) - qNew(i)) / T(i));
end
d(n - 3) = 6.0 * ((qNew(n) - qNew(n - 2)) / T(n - 2) - (qNew(n - 2) - qNew(n - 3)) / T(n - 3) - vn * T(n - 1) / T(n - 2) + an * T(n - 1)^2 / (3.0 * T(n - 2)));
d(n - 2) = 6.0 * ((qNew(n - 2) - qNew(n)) / T(n - 2) + vn * (1.0 + T(n - 1) / T(n - 2)) - an * (0.5 + T(n - 1) / (3.0 * T(n - 2))) * T(n - 1));
[w, sta] = solve_tridiagonal_matrix_equation(a, b, c, d, n - 2);
if sta == 0
error('三对角矩阵方程求解出错!');
end
w = [a0; w; an];
qNew(2) = qNew(1) + T(1) * v0 + T(1)^2 * a0 / 3.0 + T(1)^2 * w(2) / 6.0;
qNew(n - 1) = qNew(n) - T(n - 1) * vn + T(n - 1)^2 * an / 3.0 + T(n - 1)^2 * w(n - 1) / 6.0;
time = [];
pos = [];
vel = [];
acc = [];
time = [time; t(1)];
pos = [pos; qNew(1)];
vel = [vel; v0];
acc = [acc; a0];
for i = 1 : n - 1
tt = (t(i) + deltaT : deltaT : t(i + 1))';
b0 = qNew(i);
b1 = (qNew(i + 1) - qNew(i)) / T(i) - T(i) * (w(i + 1) + 2.0 * w(i)) / 6.0;
b2 = 0.5 * w(i);
b3 = (w(i + 1) - w(i)) / (6.0 * T(i));
time = [time; tt];
pos = [pos; b0 + (tt - t(i)) .* (b1 + (tt - t(i)) .* (b2 + b3 .* (tt - t(i))))];
vel = [vel; b1 + (tt - t(i)) .* (2.0 * b2 + 3.0 * b3 .* (tt - t(i)))];
acc = [acc; 2.0 * b2 + 6.0 * b3 .* (tt - t(i))];
end
if abs(time(end) - t(n)) > 1.0e-8
time = [time; t(n)];
pos = [pos; qNew(n)];
vel = [vel; vn];
acc = [acc; an];
end
figure(1)
subplot(3, 1, 1)
plot(time, pos);
hold on
plot(t([1, 3 : n - 2, n]), q, 'ro');
plot(t([2, n - 1]), qNew([2, n - 1]), 'bs');
xlabel('t')
ylabel('pos')
subplot(3, 1, 2)
plot(time, vel);
hold on
plot(t([1, n]), [v0, vn], 'ro');
xlabel('t')
ylabel('vel')
subplot(3, 1, 3)
plot(time, acc);
hold on
plot(t([1, n]), [a0, an], 'ro');
xlabel('t')
ylabel('acc')
四、参考文献
Trajectory Planning for Automatic Machines and Robots中章节:4.4.5 Smoothing cubic splines