7、树、二叉树以及代码构建

本篇博客部分图片来自《黑马程序员数据结构资料》，如有侵权，请联系我。

树

1、树的基本定义

树是我们计算机中非常重要的一种数据结构，同时使用树这种数据结构，可以描述现实生活中的很多事物，例如家 谱、单位的组织架构、等等。

树是由n（n>=1）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就 是说它是根朝上，而叶朝下的。

1.1 树的相关术语

略，自行CSDN搜索；

2、二叉树

二叉树就是度不超过2的树(每个结点最多有两个子结点)
每个节点有且最多有两个节点

2.1 平衡二叉树

选择任任意一个根节点，左子树总结点的个数与右子树总结点的个数的差的绝对值不超过1。

2.2 满二叉树

一个二叉树，如果每一个层的结点树都达到最大值，则这个二叉树就是满二叉树。

2.3 完全二叉树

叶节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树

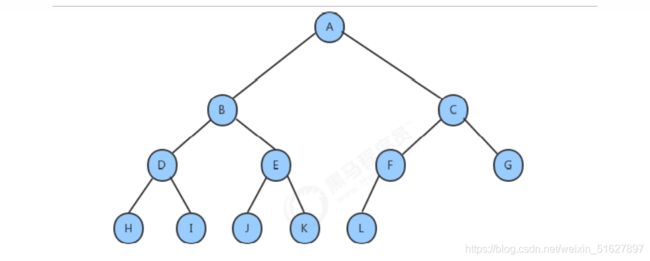
3、二叉树的遍历

3.1 前序、中序、后续遍历

我们把树简单的画作上图中的样子，由一个根节点、一个左子树、一个右子树组成，那么按照根节点什么时候被访 问，我们可以把二叉树的遍历分为以下三种方式：
1、前序遍历:先访问根结点，然后再访问左子树，最后访问右子树。
2、中序遍历:先访问左子树，中间访问根节点，最后访问右子树。
3、先访问左子树，再访问右子树，最后访问根节点。
如果我们分别对下面的树使用三种遍历方式进行遍历，得到的结果如下：

3.2 代码实现

void travel(struct node_st *root)
{
        
    if(root == NULL)
        return ;
    
//  print_s(&root->data);    //先序遍历
    travel(root->l);
//  print_s(&root->data);     //中序遍历
    travel(root->r);
    print_s(&root->data);     //后序遍历
}

4、二叉树的创建(代码实现)

通常用链式结构进行存储，这样比较节省空间。

3.1 结点的程序设计

创建一个结构体，包含数据域，数据域用来存放我要插入的数据。两个指针域，分别为左指针和右指针。如上图所示。

#define NAMESIZE	32
struct score_st
{
     
	int id;
	char name[NAMESIZE];
	int math;
};
struct node_st
{
     
	struct score_st data;
	struct node_st *l,*r;
};

用递归的方法进行实现，

3.2 插入数据_insert.c(struct node_st **,struct score_st *)

//为什么要传二级指针
//每一个节点都是相对的，每一次调用二级指针所指向的一级目标都不一样.
int insert(struct node_st **root, struct score_st *data)
{
     
	struct node_st *node;
//
	if(*root == NULL) //如果当前结点没有数据，就直接进行插入
	{
     
		node = malloc(sizeof(*node));
		if(node == NULL)
			return -1;
		node->data = *data;
		node->l = node->r = NULL;
		*root = node; //让头指针指向新的节点
		return 0;
	}
	//如果待插入的信息小于或等于现有的根节点当中的信息时，就在再次递归往左面找。
    //否则就沿着当前结点的右孩子进行比较
	if(data->id <=  (*root)->data.id)  
		return insert(&(*root)->l,data);
	return insert(&(*root)->r,data);
}

3.3 查找数据_find(struct node_st *, int )

struct score_st *find(struct node_st *root, int id)
{
     
	if(root == NULL)
		return NULL;
	if(root->data.id == id)
		return &root->data; //返回的是一个地址

	if(id < root->data.id)
		return find(root->l,id);
	return find(root->r,id);
}

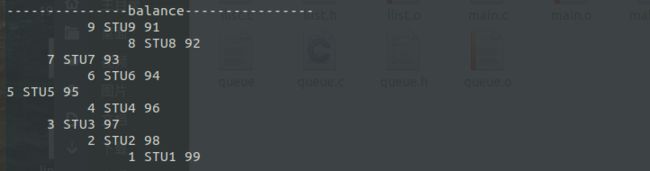
3.4 实现打印输出_draw(struct node_st *)

打印输出递归思想示意图：

static void draw_(struct node_st *root,int level)
{
     
    int i;
    if(root == NULL)
        return ;

    draw_(root->r,level+1); //level是层数
    for(i = 0;i < level;i++) //在第几层就打印几段空格
        printf("    ");
    print_s(&root->data);

    draw_(root->l,level+1);
}
void draw(struct node_st *root)
{
     
    draw_(root,0);
}

3.5 实现平衡二叉树的转换

根需要被更新，所以函数需要传一级指针的地址，而且左右指针也会改变指向，在使用函数时，就需要用二级指针来接收。

//计算节点的总数，如果传根的左结点就是计算二叉树左面所有节点的个数
static int get_num(struct node_st *root)
{
     
	if(root == NULL)
		return 0;
	return get_num(root->l) + 1 + get_num(root->r);
}
//递归寻找结点的左子树为空的节点，然后返回
static struct node_st *find_min(struct node_st *root)
{
     
	if(root->l == NULL)
		return root;
	return find_min(root->l);
}
//左旋函数，如果左面的节点少，就左旋
static void turn_left(struct node_st **root)
{
     
	struct node_st *cur = *root;

	*root = cur->r;
	cur->r = NULL;
	find_min(*root)->l = cur;

//	draw(tree);
}
//递归寻找结点的右子树为空的节点，然后返回
static struct node_st *find_max(struct node_st *root)
{
     
	if(root->r == NULL)
		return root;
	return find_max(root->r);
}  
//右旋函数，如果右面的节点少，就右旋
static void turn_right(struct node_st **root)
{
     
	struct node_st *cur = *root;

	*root = cur->l;
	cur->l = NULL;
	find_max(*root)->r = cur;

//	draw(tree);
}
//将二叉树变为平衡二叉树
void balance(struct node_st **root)
{
     
	int sub;

	if(*root == NULL)
		return ;

	while(1)
	{
     
		sub = get_num((*root)->l) - get_num((*root)->r);
		if(sub >= -1 && sub <= 1)
			break;
		if(sub < -1) 
			turn_left(root);
		else
			turn_right(root);
	}

	balance(&(*root)->l);
	balance(&(*root)->r);
}

输出：

3.6 按层次遍历二叉树_travel1(struct node_st *root)

所谓的层序遍历，就是从根节点（第一层）开始，依次向下，获取每一层所有结点的值
实现步骤：
(1)、创建队列，存放每一层的结点。
(2)、先将根节点存进去
(3)、使用循环队列弹出每一个结点
如果当前结点的左子结点不为空，，则把左子结点放入到队列中
如果当前结点的右子结点不为空，则把右子结点放入到队列中

void travel1(struct node_st *root)
{
     
    QUEUE *qu;
    struct node_st *new;
    qu = queue_create(sizeof(struct node_st *));
    /* if error*/
    queue_en(qu,&root);

    while(1)
    {
     
        if(queue_de(qu,&new) != 0) //出队，并且把对顶的元素存到new中去
            break;
        print_s(&new->data);
        if(new->l != NULL) //如果当前结点的左子结点不为空
            queue_en(qu,&new->l);
        if(new->r != NULL) //如果当前结点的右子结点不为空
            queue_en(qu,&new->r);

    }
    queue_destroy(qu);
}

3.7 删除二叉树上的某一结点

代码比较乱，自己研究吧，不讲了

void delete(struct node_st **root,int id)
{
        
    struct node_st *p,*fp;
    
    struct node_st *dele ;
    dele = find_de(*root,id);
    if(find_de(*root,id) == NULL || *root == NULL)
    {
     
        printf("Can not find\n");
    } 
    p = *root; 
    while(1)
    {
     
        fp = p;
        if(p->data.id > id) p = p->l;
        if(p->data.id < id) p = p->r;
        if(p->data.id == id) break;
    }
    //删除叶子结点
    if(p->l == NULL && p->r == NULL)
    {
     
        if(p == *root)
        {
     
            free(*root);
            return ;
        }
        if(fp->l == p)
        {
     
            fp->l = NULL;
            return ;
        }
        if(fp->r == p)
        {
     
            fp->r = NULL;
            return ;
        }
    
    }
    
    dele->data = dele->l->data;
    find_max(dele->l)->r = dele->r;
    dele->r = dele->l->r;
    dele->l = dele->l->l;
}