拓扑排序在顶尖风控团队的业务落地

你好，我是小黄，一名独角兽企业的Java开发工程师。
感谢茫茫人海中我们能够相遇，
俗话说：当你的才华和能力，不足以支撑你的梦想的时候，请静下心来学习，
希望优秀的你可以和我一起学习，一起努力，实现属于自己的梦想。

一、引言

上一章我们讲解了关于图的搜索方法，主要是深度优先搜索和广度优先搜索，两种方法的搜索方式各有优点

不知道大家在日常工作中有没有碰到这种情况：

比如，我们只有完成工作一之后，才能去完成工作二、工作三，当工作二和工作三同时完成时，我们的工作四才开始开始

简单来说，当前工作必须依赖别的工作完成之后，才能实施工作，那么我们怎么判断哪一份工作需要提前完成呢？

这就是我们今天要讲的 拓扑排序

二、什么是拓扑排序

在图论中，拓扑排序（Topological Sorting）是一个有向无环图的所有顶点的线性序列。

且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图才有拓扑排序，有环图没有拓扑排序一说

对于上图来说，拓扑排序可以帮我们做点什么呢？

• 分析每一个点的前后完成的位置
• 判断该图是否有环无环

三、拓扑排序的风控落地

在常见的风控公司，有这样一个功能：决策流

简单来说，用户通过配置规则、dubbo服务，做一个流式的计算，如图所示：

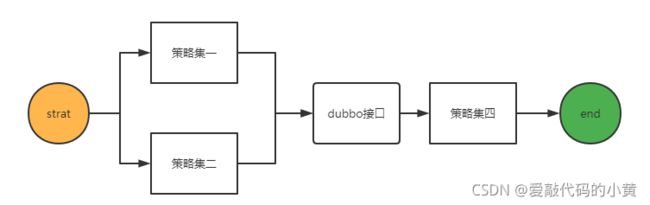
这是一个比较简单的决策流，它由三个策略集编排，并有起始和结束，是符合BPMN规范的

我们的决策流在执行时，通过拓扑排序去判断每一个策略集完成的前后顺序，进行决策的判断

而dubbo接口的作用，通过远程服务调用，获取我们需要的信息去进行决策的判断，最终获取一个分数

四、决策流的实现代码

组装成图的思路可见：给我5分钟，带你秒杀所有图算法之图的对象化描述

拓扑排序的思路：对于当前图中入度为0的点，即为当前可以执行操作的点

简单理解就是：当前的点，没有人指向他

对于上述思路，我们简单的遍历一遍所有点，可以得出第一次需要执行的点

当我们把第一个点给使用掉之后，我们需要将该点所连接的点的入度减一

我们直接看下代码：

	public static void getScore(DecisionFlowGraph graph, HashMap<String, String> map) {
     
        // 使用一个队列
        Queue<DecisionFlowPoint> queue = new LinkedList<>();

        // 遍历所有的点，找到入度为 0 的点
        for (DecisionFlowPoint point : graph.points.values()) {
     
            // 入度为0
            if (point.in == 0) {
     
                queue.add(point);
            }
        }
        
        // 当前的队列不为空
        while (!queue.isEmpty()) {
     
            // 弹出当前队列的头
            DecisionFlowPoint point = queue.poll();
            // 使用当前该点代表的策略集
            finalScore = finalScore + resolve(point, map);
            // 将该点所连接的点的入度减一
            for (DecisionFlowPoint next : point.points) {
     
                next.in--;
                if (next.in == 0) {
     
                    queue.add(next);
                }
            }
        }
    }

整个流程的代码由于太长的原因，在这里就不展示了，有兴趣的可以公众号回复：算法源码

不仅包括图的源码，还包括如下内容：

展示下最终的使用情况：

四、总结

简单来说，拓扑排序在我们实际业务中，用到的场景也是挺多的

比如：文中提到的决策流、工作流等

当然，看完本篇文章之后，也需要大量的场景去进行练习，不然容易生疏

• 题目一：207. 课程表
• 题目二：210. 课程表 II
• 题目三：1436. 旅行终点站

本期的内容就到这里，下期将会讲述 最小生成树（Prim、Kruskal） 算法。

我是一名独角兽企业的Java开发工程师，希望可以点个关注呀，有问题可以留言或者私信加我微信，我们下期再见！