- 前言
- 队列的定义
- 队列的抽象数据类型
- 循环队列与链式队列对比
- 循环队列
- 特点
- 定义
- 循环队列相关计算
- 链式队列
- 定义
- 阻塞队列
- 并发队列
- 代码实现
- 循环队列代码
- 链式队列实现
前言
李柱明博客:https://www.cnblogs.com/lizhuming/p/15487349.html
队列的定义
队列(queue)-- 只允许在一端进行插入操作,而在另一端进行删除操作的线性表:
- FIFO:先进先出的线性表。
- 允许插入的一端称为队尾,允许删除的一端称为队头。
注意:队列同样是线性表,也有类似线性表的各种操作。只是插入只能在队尾,删除只能在队头。
队列的抽象数据类型
队列的抽象数据类型可由两种实现:
- 顺序队列:由数组或指针实现。
- 链式队列:由链表是实现。
循环队列与链式队列对比
时间上:都是 O(1)。
空间上:
- 循环队列:事先申请好空间,使用期间不释放。
- 链队列:每次申请和释放结点也会存在一些时间开销。
- 循环队列:固定长度,故存在存储元素个数和空间浪费的问题。
- 链队列:需要指针域,产生一些空间上的开销,在空间上更灵活。
循环队列
特点
循环队列由数组实现。但是数组是有局限性的,所以循环队列有以下特点:
-
当队头固定设为数组下标为 0 的位置时:入队 O(1),但出队 O(n)。
-
当不限制队头必须在数组下标为 0 的位置时,可以提高一些性能。
- 需要引入两个下标。对头和队尾。
-
采用游标&循环方式:
- 引入两个指针,队头和队尾。
- 循环方式,即是如队尾溢出时便调到数组头继续。
定义
循环队列的定义:
-
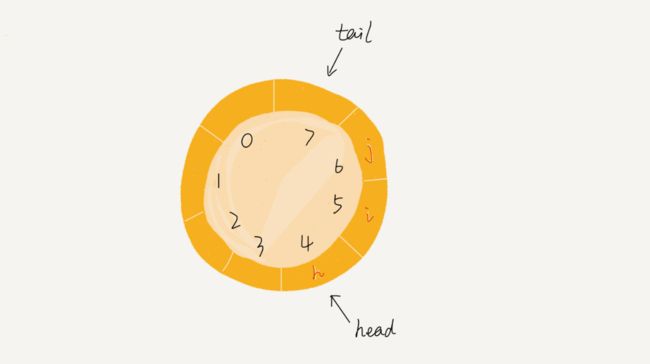
队列的头尾相接的顺序存储结构称为循环队列。
- 可以理解为数组尾就是数组头,把头尾接驳。
循环队列相关计算
计算:
-
队列 size:queue_size
-
队列空判断:head == tail
-
队列长度计算:(tail - head + QueueSize) % queue_size
-
队列满判断:head == (tail + 1) % queue_size
- 整个队列需要保留一个空的元素。
-
入队:tail = (tail + 1) % queue_size
-
出队:head = (head +1) % queue_size
链式队列
定义
链式队列:
- 队列的链式存储结构,其实就是线性表的单链表,但只能尾进头出,简称链队列。
- 本笔记的 demo 需要一个哨兵。即是头结点。哨兵为空节点(逻辑上不作为数据空间),有
queue->head指向。 - 队头指针指向链队列的头结点,队尾指针指向终端结点。
- 空队列:head 和 tail 都指向头结点。
无哨兵链式队列:
有哨兵链式队列:
阻塞队列
阻塞队列:
-
就是在队列基础上增加了阻塞操作。
-
出队:当队列为空时,出队阻塞。
-
入队:当队列满时,入队阻塞。
-
可参考 FreeRTOS,采用链表方式维护被阻塞的线程。
-
如有数据入队正常入队后,检查出队阻塞链表,阻塞链表中优先级最高的任务解除阻塞。
- 把需要解除的任务的事件节点从消息队列的等待接收链表中移除。
- 把需要解除的任务的状态节点从延时链表中移除,并插入到就绪链表中。
-
若数据入队阻塞,则:
- 把当前任务的事件节点插入到该队列的等待发送链表中。
- 把当前任务的状态节点从就绪链表移除,并插入到延时链表中。(RTOS 会实时检查延时链表)
-
注意:出队阻塞超时时,该任务会恢复就绪态,并在获得 CPU 权限后继续执行入队操作,看 API
BaseType_t xQueueReceive();可知,恢复执行后便检查任务超时时间是否到期,若到期了,就把当前任务的事件节点从消息队列等待接收链表中移除,并返回错误码。
-
并发队列
并发队列:
- 线程安全的队列叫作并发队列。
- 可以通过锁机制实现线程安全,意思是给队列配个锁。
- 但是锁粒度大并发度会比较低,同一时刻仅允许一个存或者取操作。
- 基于数组的循环队列,利用 CAS(Compare And Swap) 原子操作,可以实现非常高效的并发队列。
代码实现
循环队列代码
/** @file queue.c
* @brief 简要说明
* @details 详细说明
* @author lzm
* @date 2021-09-10 21:12:56
* @version v1.0
* @copyright Copyright By lizhuming, All Rights Reserved
* @blog https://www.cnblogs.com/lizhuming/
*
**********************************************************
* @LOG 修改日志:
**********************************************************
*/
#include
#include
#include
// 建议把本文件修改成循环队列的底层文件。
// 创建时,上层提供原数类型大小和最大个数即可。
// 而本文件的队列空间颗粒改为一个字节。
// 循环队列
typedef int qe_type; /* 元素类型 */
#define QUEUE_SIZE 100 /* 栈元素个数 */
typedef struct
{
qe_type data[QUEUE_SIZE]; /* 空间 */
int head; /* 头指针 */
int tail; /* 尾指针 */
}queue_array_t;
/**
* @name queue_creat
* @brief
* @param
* @retval
* @author lzm
*/
queue_array_t *queue_array_creat(void)
{
queue_array_t *queue_ptr = NULL;
queue_ptr = (queue_array_t *)malloc(sizeof(queue_array_t));
if(queue_ptr == NULL)
return NULL;
memset(queue_ptr, 0x00, sizeof(queue_array_t));
queue_ptr->head = 0;
queue_ptr->tail = 0;
return queue_ptr;
}
/**
* @name queue_destroy
* @brief
* @param
* @retval
* @author lzm
*/
int queue_destroy(queue_array_t *queue)
{
if(queue != NULL)
{
free(queue);
return 0;
}
return -1;
}
/**
* @name queue_clear
* @brief
* @param
* @retval
* @author lzm
*/
int queue_clear(queue_array_t *queue)
{
if(queue == NULL)
return -1;
queue->head = 0;
queue->tail = 0;
return 0;
}
/**
* @name queue_empty
* @brief
* @param
* @retval
* @author lzm
*/
int queue_empty(queue_array_t *queue)
{
if(queue == NULL)
return -1;
if(queue->head == queue->tail)
return 1;
return 0;
}
/**
* @name queue_full
* @brief
* @param
* @retval
* @author lzm
*/
int queue_full(queue_array_t *queue)
{
if(queue == NULL)
return -1;
if(queue->head == (queue->tail + 1) % QUEUE_SIZE)
return 1;
return 0;
}
/**
* @name queue_length
* @brief
* @param
* @retval
* @author lzm
*/
int queue_length(queue_array_t *queue)
{
if(queue == NULL)
return -1;
return (queue->tail - queue->head + QUEUE_SIZE) % QUEUE_SIZE;
}
/**
* @name queue_insert
* @brief
* @param
* @retval
* @author lzm
*/
int queue_insert(queue_array_t *queue, qe_type elem)
{
if(queue_full(queue) != 0)
return -1;
queue->data[queue->tail] = elem;
queue->tail = (queue->tail + 1) % QUEUE_SIZE;
return 0;
}
/**
* @name queue_delete
* @brief
* @param
* @retval
* @author lzm
*/
int queue_delete(queue_array_t *queue, qe_type *elem)
{
if(queue_empty(queue) != 0 || elem == NULL)
{
return -1;
}
*elem = queue->data[queue->head];
queue->head = (queue->head + 1) % QUEUE_SIZE;
return 0;
}
/**
* @name queue_get_top
* @brief
* @param
* @retval
* @author lzm
*/
int queue_get_head(queue_array_t *queue, qe_type *elem)
{
if(queue_empty(queue) != 0 || elem == NULL)
{
return -1;
}
*elem = queue->data[queue->head];
return 0;
}
链式队列实现
/** @file queue.c
* @brief 简要说明
* @details 详细说明
* @author lzm
* @date 2021-09-10 21:31:11
* @version v1.0
* @copyright Copyright By lizhuming, All Rights Reserved
* @blog https://www.cnblogs.com/lizhuming/
*
**********************************************************
* @LOG 修改日志:
**********************************************************
*/
#include
#include
#include
// 建议把本文件修改成循环队列的底层文件。
// 创建时,上层提供原数类型大小和最大个数即可。
// 而本文件的队列空间颗粒改为一个字节。
/* 链式结构 */
typedef int qe_type; /* 元素类型 */
typedef struct queue_node
{
qe_type date;
struct queue_node *next;
}queue_node_t;
typedef struct
{
queue_node_t *head; /* 哨兵 */
queue_node_t *tail; /* 队尾 */
}queue_link_t;
/**
* @name queue_link_creat
* @brief 使用了哨兵方式
* @param
* @retval
* @author lzm
*/
queue_link_t *queue_link_creat(int size)
{
queue_link_t *queue_ptr = NULL;
queue_ptr = (queue_link_t *)malloc(sizeof(queue_link_t));
if(queue_ptr == NULL)
return NULL;
memset(queue_ptr, 0x00, sizeof(queue_link_t));
queue_ptr->tail = (queue_node_t *)malloc(sizeof(queue_node_t));
if(queue_ptr->tail == NULL)
{
return NULL;
}
queue_ptr->head = queue_ptr->tail;
return queue_ptr;
}
/**
* @name queue_link_destroy
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_destroy(queue_link_t *queue)
{
if(queue == NULL)
return -1;
while(queue->head)
{
queue->tail = queue->head->next;
free(queue->head);
queue->head = queue->tail;
}
free(queue);
return 0;
}
/**
* @name queue_link_clear
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_clear(queue_link_t *queue)
{
queue_node_t *queue_cur = NULL;
queue_node_t *queue_last = NULL;
if(queue == NULL)
return -1;
queue->tail = queue->head;
queue_cur = queue->head->next;
queue->head->next = NULL;
while(queue_cur)
{
queue_last = queue_cur;
queue_cur = queue_cur->next;
free(queue_last);
}
return 0;
}
/**
* @name queue_link_empty
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_empty(queue_link_t *queue)
{
if(queue == NULL)
return -1;
if(queue->head == queue->tail)
return 1;
return 0;
}
/**
* @name queue_link_length
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_length(queue_link_t *queue)
{
int cnt = 0;
queue_node_t *queue_cur = NULL;
if(queue == NULL)
return -1;
queue_cur = queue->head;
while(queue_cur != queue->tail)
{
cnt++;
queue_cur = queue_cur->next;
}
return cnt;
}
/**
* @name queue_link_inster
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_inster(queue_link_t *queue, qe_type elem)
{
queue_node_t *queue_node_ptr = NULL;
queue_node_ptr = (queue_node_t *)malloc(sizeof(queue_node_t));
if(queue_node_ptr == NULL)
return -1;
memset(queue_node_ptr, 0x00, sizeof(queue_node_t));
queue_node_ptr->date = elem;
queue_node_ptr->next = NULL;
queue->tail->next = queue_node_ptr;
queue->tail = queue_node_ptr;
return 0;
}
/**
* @name queue_link_delete
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_delete(queue_link_t *queue, qe_type *elem)
{
queue_node_t *node = NULL;
if(queue_link_empty(queue) != 0 || elem == NULL)
{
return -1;
}
node = queue->head->next;
*elem = node->date;
queue->head->next = node->next;
if(node == queue->tail)
queue->tail = queue->head;
free(node);
return 0;
}
/**
* @name queue_link_get_top
* @brief
* @param
* @retval
* @author lzm
*/
int queue_link_get_top(queue_link_t *queue, qe_type *elem)
{
if(queue_link_empty(queue) != 0 || elem == NULL)
{
return -1;
}
*elem = queue->head->next->date;
return 0;
}