第四届浙江省大学生网络与信息安全竞赛（预赛）Crypto方向WP

原文地址

https://4xwi11.github.io/posts/a2deb6fa/#more

浙江省赛复现

首先看下机房别的地方ipv4的配置，然后拿来换一个子网的地址

md，配置又搞了半天，实验室请别人分配的，有机会一定学下网络

Crypto

Easy Railfence

尝试分析逻辑失败，或者说要花的时间不值得

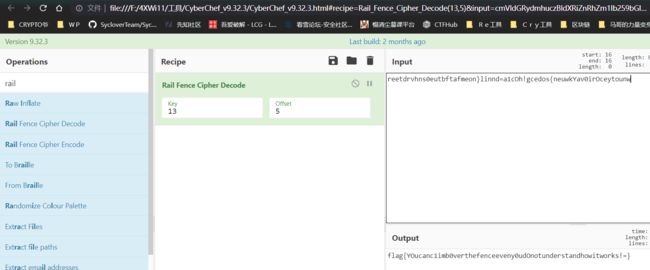
题目提示Rail，key和offset未知，那么直接手撕

flag{YOucanc1imb0verthefenceeveny0udOnotunderstandhowitworks!=}

import hashlib

m = b'flag{YOucanc1imb0verthefenceeveny0udOnotunderstandhowitworks!=}'

flag = hashlib.md5(m).hexdigest()

print(flag)

a88dd8d7894a7a65dda2d4c6d44357b9

二血

EasyCrypto（recuring）

ip: 152.136.122.197
port: 52503
protocol: tcp

nc链接，好隐晦不知道干嘛，不会又和上次WM一样吧

没看到公告的附件，太卡了，拿到附件让逆向队友upx脱下壳

煞笔，出尼玛逆向题

要达到的攻击效果就是，要在login的时候，把adminadmin生成的token给发过去，但是在register阶段，不能加密任何包含admin字段的字符串

---

从头开始，先脱壳，吾爱破解吧上随便找了个工具

加壳的不能远调？

whatever脱了就行

然后尽力了，逆向做的不多，刚开始学，而且还是用C++写的，虽然比之前的伪代码好懂多（不知道是不是出题人有意为之）， 但是做到最后看不出来是哪一模式的AES

int __cdecl __noreturn main(int argc, const char **argv, const char **envp)
{
     
  v55 = __readfsqword(0x28u);                   // 开canary，跳过不影响理解
  key_unknown = GenIV();
  iv_known = GenIV();
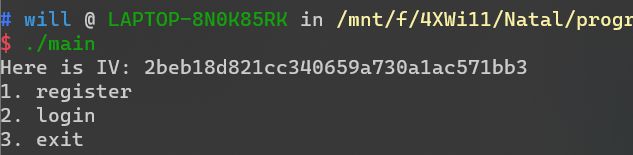
  std::operator<<<std::char_traits<char>>(&std::cout, "Here is IV: ");
  // 输出IV，每8位bin（8*16）转2位hex，填充为0，共32位
  for ( i = 0; i <= 15; ++i )
  {
     
    v3 = std::ostream::operator<<(&std::cout, std::hex);
    v4 = std::setfill<char>('0');
    v5 = std::operator<<<char,std::char_traits<char>>(v3, v4);
    v6 = std::setw(2);
    output_format = std::operator<<<char,std::char_traits<char>>(v5, v6);
    v8 = std::bitset<8ul>::to_ulong(&iv_known[i]);// 转为十进制
    std::ostream::operator<<(output_format, v8);
  }
  std::ostream::operator<<(&std::cout, &std::endl<char,std::char_traits<char>>);
  while ( 1 )
  {
     
    while ( 1 )
    {
     
      while ( 1 )
      {
     
        display();
        std::istream::operator>>(&std::cin, &choice);
        if ( choice != 1 )
          break;
        std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::basic_string(name);
        v9 = std::operator<<<std::char_traits<char>>(&std::cout, "Plz input your name: ");
        std::ostream::operator<<(v9, &std::endl<char,std::char_traits<char>>);
        std::operator>><char>(&std::cin, name);
        // 输入的name不包含"admin"，而且长度为16的倍数
        if ( std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::find(name, "admin", 0LL) != -1
          || (std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(name) & 15) != 0 )
        {
     
          v11 = std::operator<<<std::char_traits<char>>(&std::cout, "no no no");
          std::ostream::operator<<(v11, &std::endl<char,std::char_traits<char>>);
          exit(0);
        }
        v12 = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(name);
        if ( v12 > 1152921504606846975LL )
          __cxa_throw_bad_array_new_length();
        v13 = operator new[](8 * v12);
        v14 = v12 - 1;
        v15 = v13;
        while ( v14 >= 0 )
        {
     
          std::bitset<8ul>::bitset(v15);
          v15 += 8LL;
          --v14;
        }
        bin_name = v13;
        // 将name的每个字符取出来，并转成8位bin
        for ( j = 0; ; ++j )
        {
     
          v16 = j;
          if ( v16 >= std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(name) )
            break;
          v17 = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::at(name, j);
          std::bitset<8ul>::bitset(&v47, *v17);
          *(bin_name + 8LL * j) = v47;
        }
        len_name = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(name);
        encode(key_unknown, iv_known, bin_name, len_name);
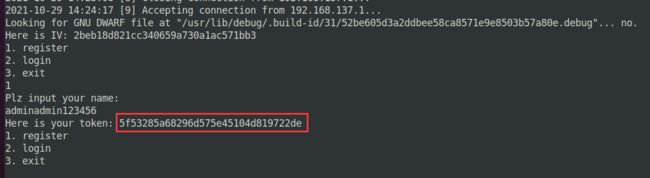
        std::operator<<<std::char_traits<char>>(&std::cout, "Here is your token: ");
        // 输出token
        for ( k = 0; ; ++k )
        {
     
          v19 = k;
          if ( v19 >= std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(name) )
            break;
          v20 = std::ostream::operator<<(&std::cout, std::hex);
          v21 = std::setfill<char>('0');
          v22 = std::operator<<<char,std::char_traits<char>>(v20, v21);
          v23 = std::setw(2);
          v24 = std::operator<<<char,std::char_traits<char>>(v22, v23);
          v25 = std::bitset<8ul>::to_ulong(8LL * k + bin_name);
          std::ostream::operator<<(v24, v25);
        }
        std::ostream::operator<<(&std::cout, &std::endl<char,std::char_traits<char>>);
        std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(name);
      }
      if ( choice != 2 )
        break;
      std::operator<<<std::char_traits<char>>(&std::cout, "Plz input your token: ");
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::basic_string(input_token);
      std::operator>><char>(&std::cin, input_token);
      // 长度必须是32的倍数
      if ( (std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(input_token) & 31) != 0 )
      {
     
        v26 = std::operator<<<std::char_traits<char>>(&std::cout, "no no no");
        std::ostream::operator<<(v26, &std::endl<char,std::char_traits<char>>);
        exit(0);
      }
      v27 = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(input_token) >> 1;
      if ( v27 > 0xFFFFFFFFFFFFFFFLL )
        __cxa_throw_bad_array_new_length();
      init = operator new[](8 * v27);
      v29 = v27 - 1;
      v30 = init;
      // 把token的每两个字符取出，并转成bin
      while ( v29 >= 0 )
      {
     
        std::bitset<8ul>::bitset(v30);
        v30 += 8LL;
        --v29;
      }
      bit_token = init;
      for ( m = 0; ; ++m )
      {
     
        v31 = m;
        if ( v31 >= std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(input_token) >> 1 )
          break;
        std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::substr(
          name,
          input_token,
          2 * m,
          2LL);
        v32 = std::__cxx11::stoi(name, 0LL, 16LL);
        std::bitset<8ul>::bitset(&v47, v32);
        *(bit_token + 8LL * m) = v47;
        std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(name);
      }
      len_token = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(input_token);
      decode(key_unknown, iv_known, bit_token, (len_token >> 1));
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::basic_string(output_name);
      // 输出解密后的token
      for ( n = 0; ; ++n )
      {
     
        v34 = n;
        if ( v34 >= std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::length(input_token) >> 1 )
          break;
        v35 = std::bitset<8ul>::to_ulong(8LL * n + bit_token);
        std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::operator+=(output_name, v35);
      }
      v36 = std::operator<<<std::char_traits<char>>(&std::cout, "Hello, ");
      v37 = std::operator<<<char>(v36, output_name);
      std::ostream::operator<<(v37, &std::endl<char,std::char_traits<char>>);
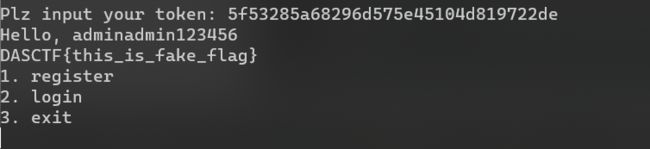
      // 从output_name中取前10个作为name
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::substr(name, output_name, 0LL, 10LL);
      tip = std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::compare(name, "adminadmin") == 0;
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(name);
      if ( tip )
      {
     
        get_flag = std::operator<<<char>(&std::cout, &flag[abi:cxx11]);
        std::ostream::operator<<(get_flag, &std::endl<char,std::char_traits<char>>);
      }
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(output_name);
      std::__cxx11::basic_string<char,std::char_traits<char>,std::allocator<char>>::~basic_string(input_token);
    }
    if ( choice == 3 )
      exit(0);
    v40 = std::operator<<<std::char_traits<char>>(&std::cout, "Wrong choice");
    std::ostream::operator<<(v40, &std::endl<char,std::char_traits<char>>);
  }
}

然后加密函数

unsigned __int64 __fastcall encode(__int64 KEY, __int64 known_iv, __int64 plaintext, int length)
{
     
  int v4; // eax
  int i; // [rsp+20h] [rbp-200h]
  int v9; // [rsp+24h] [rbp-1FCh]
  int j; // [rsp+28h] [rbp-1F8h]
  int k; // [rsp+2Ch] [rbp-1F4h]
  __int64 iv[16]; // [rsp+30h] [rbp-1F0h] BYREF
  char key[360]; // [rsp+B0h] [rbp-170h] BYREF
  unsigned __int64 v14; // [rsp+218h] [rbp-8h]

  v14 = __readfsqword(0x28u);
  memset(key, 0, 352uLL);
  KeyExpansion(KEY, key);
  memset(iv, 0, sizeof(iv));
  for ( i = 0; i <= 15; ++i )
    iv[i] = *(known_iv + 8LL * i);
  v9 = 0;
  for ( j = 0; j < length; ++j )
  {
     
    encrypt(iv, key);
    std::bitset<8ul>::operator^=(plaintext + 8LL * v9, iv);
    for ( k = 0; k <= 14; ++k )
      iv[k] = iv[k + 1];
    v4 = v9++;
    iv[15] = *(8LL * v4 + plaintext);
  }
  return __readfsqword(0x28u) ^ v14;
}

解密函数

unsigned __int64 __fastcall decode(__int64 a1, __int64 a2, __int64 a3, int a4)
{
     
  int v4; // eax
  int i; // [rsp+24h] [rbp-20Ch]
  int v9; // [rsp+28h] [rbp-208h]
  int j; // [rsp+2Ch] [rbp-204h]
  int k; // [rsp+30h] [rbp-200h]
  int v12; // [rsp+34h] [rbp-1FCh]
  __int64 v13; // [rsp+38h] [rbp-1F8h] BYREF
  __int64 v14[16]; // [rsp+40h] [rbp-1F0h] BYREF
  char v15[360]; // [rsp+C0h] [rbp-170h] BYREF
  unsigned __int64 v16; // [rsp+228h] [rbp-8h]

  v16 = __readfsqword(0x28u);
  memset(v15, 0, 0x160uLL);
  KeyExpansion(a1, v15);
  memset(v14, 0, sizeof(v14));
  for ( i = 0; i <= 15; ++i )
    v14[i] = *(a2 + 8LL * i);
  v9 = 0;
  for ( j = 0; j < a4; ++j )
  {
     
    encrypt(v14, v15);
    v12 = std::bitset<8ul>::to_ulong(8LL * v9 + a3);
    v4 = v9++;
    std::bitset<8ul>::operator^=(a3 + 8LL * v4, v14);
    for ( k = 0; k <= 14; ++k )
      v14[k] = v14[k + 1];
    std::bitset<8ul>::bitset(&v13, v12);
    v14[15] = v13;
  }
  return __readfsqword(0x28u) ^ v16;
}

可以看出是AES，感觉是CFB？

借一下上次的图

我觉得已知IV，根据重排攻击，搞出E_KEY(IV)，应该不难，然后另起炉灶，用IV和KEY加密以adminadmin开头的明文，再send过去就好了

吧

之前字节CTF就做到类似的，看V神的博客知道怎么攻击，可惜没实现

然后网上搜到翻车鱼师傅的博客

https://blog.shi1011.cn/ctf/1700

寄

虽然比赛的想到绕过if，让逆向队友帮nop了一下，但是机智的我想改了本地有毛用，服务器没变啊

。。。忘了可以在动调的时候直接改内存，把本地的IV改成服务器跑的IV，然后加密adminadmin填充成16长度的字符

emmmmmm逆向的基本素质不够，归结于这方面做的不多

看着师傅的博客一边复现一边学

---

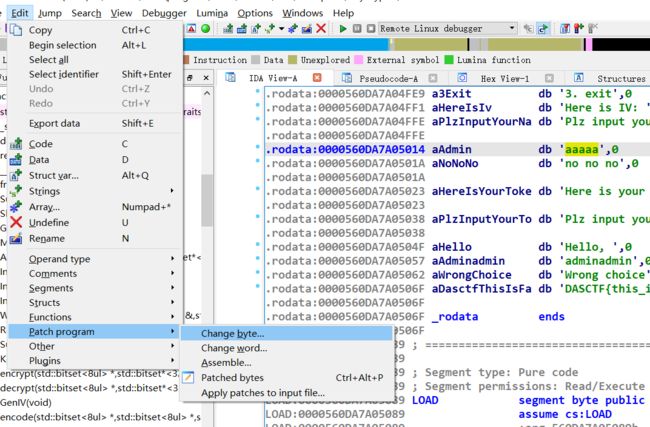
绕过加密的if，将admin字符串改成别的

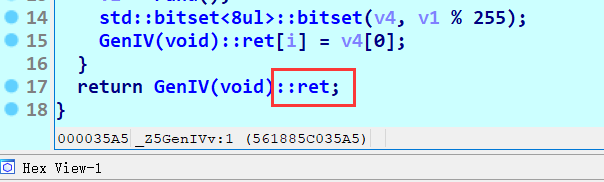
再在GenIV的时候下个断点，远程调试，步入GenIV

这里还有一点二进制方向的点，就是IV和KEY其实是同一个，动调也可以看出在加密的时候两个寄存器的值其实是一样的

原因主要是和这个有关系吧

返回的这个是一个全局变量；所以我们一定要步入，在return之前把0x561885e08300处的值给改成服务器的IV

可以像师傅那样写个脚本放进ida，也可以。。。emmmmm按理说也可以手动patch掉啊，没成功，以后再说

偷下脚本

addr = 0x55DF1EE08300  # patch address
test = "2beb18d821cc340659a730a1ac571bb3"  # patch hex data
ps = [i for i in b''.fromhex(test)]
for i, v in enumerate(ps):
    ida_bytes.patch_qword(addr+i * 8, v)

反正就是把这些数据给换成连上服务器的IV

IV和KEY都要改

可以看到

两个IV是一样的了，现在是要加密adminadmin后面随便填充满16个字符

把加密的结果给服务器，就获得flag啦

当然这是本地的

挺好的，懂一点二进制的知识，也不是很难，200分还凑合吧，因为没有涉及到密码攻击

可信计算1（recuring）

密码体制是可信计算的基础，我国可信计算密码体制借鉴国际先进的可信计算技术框架与技术理念并自主创新,是构建我国可信计算技术规范体系的基础。非对称密码算法采用的椭圆曲线密码算法. 包括三个子算法: 椭圆曲线数字签名算法(SM2-1)、椭圆曲线密钥交换协议(SM2-2)、椭圆曲线公钥加密算法(SM2-3). 对称密码算法采用SM-4算法。差分故障分析攻击是一种强大的密码分析技术，可通过利用加密（解密）过程中的计算错误来检索密钥。我国科研人员提出了使用单一故障（single fault）对SMS4（即SM4）进行新的攻击。黑客利用此攻击获得了密钥并且再经过了一系列RSA加密。你能重新解密它吗？

给了篇论文，让我们填代码，xs

要完整一个attack脚本得到solution()的值，然后解RSA，得到的明文和solution()的值异或就是flag

离比赛结束还有一个四五十分钟左右上了提示，相当于告诉了我们solution()的值，所以只要解RSA就好了

（所以本来300分的题目，现在顶多200吧

第二个n很奇怪，中间有很多0，显然是有意构造的，尝试，然后用Williams’s p+1 光滑数分解出来了

最后要求d

---

我们现在相当于知道$n\times D\equiv 1(modlcm(p-1,q-1))$，要求$n\times d\equiv 1(mod\phi (n))$，其中$n=p^{2}q$

我的思路是和dp泄露攻击那样，将上式写成
$$n\times D=1+k\times \frac{(p-1)(q-1)}{gcd(p-1,q-1)}$$
但是$k$的位数是朝$n$看齐的，$n$太大了

赛后给老韩看了这题，然后就出了

前导知识

改进版欧拉定理

$n=pq$

欧拉定理：如果$ed\equiv 1(mod\phi (n))$，则$m^{ed}\equiv m(modn)$

改进版欧拉定理：如果$ed\equiv 1(modlcm(p-1,q-1))$，则$m^{ed}\equiv m(modn)$

证明…

按理说只要把$e\times d=1+k\frac{\phi (n)}{(p-1,q-1)}$中的$\frac{k}{(p-1,q-1)}$当成一体就好了，但$(p-1,q-1)|k$成立吗

emmmmm验证了下$(p-1,q-1)|k$确实不一定成立，但可能$e\times d=1+k\frac{\phi (n)}{(p-1,q-1)}$这个等式还是成立的吧，虽然涉及到了实数域

---

所以由$n\times D\equiv 1(modlcm(p-1,q-1))$以及改进版的欧拉定理可知，随便取一个底数$a=2$
$$a^{n\times D}\equiv a(modpq)$$
即
$$a^{n\times D}-a=kpq$$
所以$(a^{nD},n)=pq$，成功分解$n$

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
import gmpy2

solution = 294165584142200864568246241265541097157

n1 = 4405077945973437035419287286810342680467164824994445863017287425857718058064367794640412586853078343089682257199040398279405943520831910368411272144036263290429027279134620341369472867932142748943900939370411886210476130066241817638604325934138989972586283462534982142208555273727206617309988865793455361561026132931733994626398919219203496779449010438682739786866247084252598908907212620561764983861943789642115256382514700516697279459245070020692018083897351520741894187752652555621713799960889861847955471596042981878988930182754796995540025157400222655523547124372140444854366346125175141685537518528913398362475082963023550518705007434135499146966555320343509832799572533328142914873980714083464226641803937211470059111827905761731285053449287872425538901604516967439734828113276097444621288760780510574237036765614111782882785171493934512613063976597374878482039022229525679671485667155329416043448757872980255141203521
c1 = 2040470907728559562144837701471699958842886502924143170940951920300330705469920644505358508388311496777477054764995077035235698658575174832523551852726014373980149374239009390776201109902621711966732796749320068316711336025560029911784168004125304818031813523186592291392842343696718617379290904175534035887756216695721678801280463979349357202298738101109440012007130354993844420187364636715038757505869998163074221607302922729567651885580362184785959736170342652272664233424398501795600338328896721625926411402939719604380362340818655911893820365244157271443958395915293530188623023020308158679057671088211570631031550074345806554689087361996299749696847678943351283609450756224172170448677652692971780286821516767097534780167858067007235131095286410071429519192415627585362097426875776726171657935230143030934637299115037016218434359722137587559402819756667711939086772125532873443844710837902048558986519222802598324087583

n = 3361086170602976142504997268236060982692605108576474794795911687547279286733833098612106940194747346221692033159371528530653580115390416679967729710739174614379783218150098775149592689781035438321880866528914504243891928775112620156291222559241186219350045576860324184984735637154578516733940554948973282721369434595704714389150209345475950609404181675208130514911232000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000097508979015194291132949514722911166191363461601383827147483675839887898302732717796964400033872583058988279308060265340699924854046743595567336710903145223470556072888621727183623668024948924590490882481168049365076186311734867473877377902845426106748782634088122150575479955070755466863095062214590909653863
c = 598528858874810608065902501620874503014983670463266646290832635056421227205733327736057508619507831133535572690260972254673128968946338072045290665489556437771583204624715681429388530078963430052969789886108472984729092440081160180316457652683648340266414640837170058066574014124614892099724102821458274691436449398719884109828222614007036994527592436185050484088075330462117248110919293447235934889162344407129203590386811121673967605695147649017737632402213023246402884535810392728946424610066090206055089489564077161138777977263714359210319267561616696663416315333732256499607636067924154333627546883589391082646997265511574165830249101937578220829206006989141322034410996411299176651062407272902632250281656652195986385298937692081569486464058189515727080309131120211009473690551213672202034941099429474075795457621831397212467951367964925257121811464825340910886150457508279599024005394220037658075742792005357721304591247193598733190937420575987082139043012560262600423787438345332029289463428943040573800279205970491450959972460765085149920791397381555581880453992

# 34469504291284154037699166143795871571814385224074410328064000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 97508979015194291132949514722911166191363461601383827147483675839887898302732717796964400033872583058988279308060265340699924854046743595567336710903145223470556072888621727183623668024948924590490882481168049365076186311734867473877377902845426106748782634088122150575479955070755466863095062214590909653863
p = 97508979015194291132949514722911166191363461601383827147483675839887898302732717796964400033872583058988279308060265340699924854046743595567336710903145223470556072888621727183623668024948924590490882481168049365076186311734867473877377902845426106748782634088122150575479955070755466863095062214590909653863
q = 34469504291284154037699166143795871571814385224074410328064000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001
phi = (p-1)*(q-1)
assert n == p * q
e = 0x10001
D = gmpy2.invert(e, phi)
d = pow(c, D, n)
pq = gmpy2.gcd(n1, (pow(2, n1*d, n1)-2) % n1)
P = n1 // pq
Q = n1 // (P ** 2)
assert P ** 2 * Q == n1
fake_phin1 = (P-1)*(Q-1)
d = gmpy2.invert(n1, P-1)
flag = long_to_bytes(pow(c1, d, P) ^ solution)
print(flag)

flag{59814ae119dc9d7c29285fde41236f77}