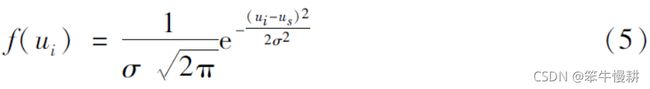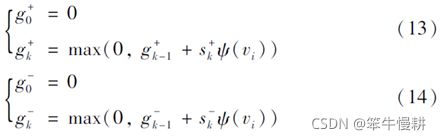论文笔记：基于复合滑动窗的CUSUM暂态事件检测算法

目录

1. 前言

2. 双边CUSUM算法原理

3. 基于复合滑动窗的暂态事件检测

3.1 高斯加权平均

3.2 检测窗口的Sigmoid处理

 3.3 检测暂态过程起止位置

4. Summary

---

1. 前言

        本文是对以下论文的解读笔记。注意在下文中“该论文”和“本文”是指向不同的对象。

        史帅彬等：基于复合滑动窗的CUSUM暂态事件检测算法, 电测与仪表2019年9月10日

        在非侵入式负荷监测中，暂态特征和稳态特征是负荷辨识的两类重要特征，稳态特征主要通过电器平稳运行之后的电流、功率特性对负荷类型进行判断，当出现混叠情况时就容易产生错误。暂态特征即不同类型的负荷在投切过程中表现出的独特的暂态特征信息。暂态特征信息由于出现混叠（[chenxy]恰好多个电器同时开或关的碰撞事件可以认为很低）的情况较少，因此是一种理想的用电设备特征表示方法，尤其是用电设备开启瞬间所发生的电流、电压信息，可以作为用电设备重要的标签。[chenxy]那电器关断时的电流电压信息呢？

        因此暂态事件检测在非侵入式负荷监测中具有重要的作用。对于暂态事件的检测，国内外有许多学者进行研究。有采用差分的方法，通过监测变量是否超过阈值判断是否有暂态事件发生。Shaw等提出了通过滑动窗口的平均值来判断是否有暂态事件发生，提高了抗噪声干扰的能力。牛卢璐提出了基于滑动窗的双边累计和暂态事件自动检测算法，这种算法简单实用，稳定性强。关于牛卢璐论文（以下简称“牛文”）的解读参见另一篇博客：

论文笔记：一种适用于NILM的暂态事件检测算法https://blog.csdn.net/chenxy_bwave/article/details/121145889

        [chenxy]本文其实可以看作是基于“牛文”的改进（？）

2. 双边CUSUM算法原理

        考察随机时间序列：

        假设 为发生变化的时刻，定义非参数化双边CUSUM算法中统计函数如下：

         式中 和 表示当前检测点去掉噪声值影响后的正向和负向偏移量。

 

        式中 为变点前随机时间序列的平均值，通常认为是已知的（chenxy:但是在NILM应用中，该值是时变的。因此在本算法中，该值在平均窗口中进行估计）； 表示噪声值（可以表达为噪声标准差乘以一个倍数），序列小于的变化将被忽略。

        注意：虽然以上描述与“牛文”描述略有形式的不同，但是实质上是完全等价的。

3. 基于复合滑动窗的暂态事件检测

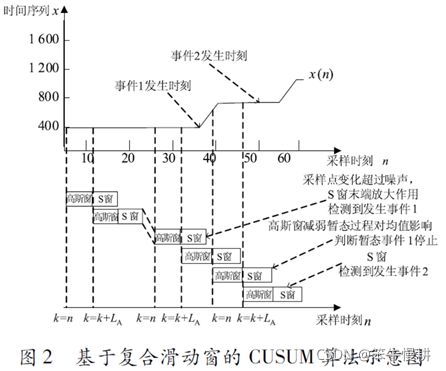
        “复合滑动窗”。。。只是一个炫酷的名字，不必在意。关于滑动窗的处理可以参见“牛文”。

        这个图也与“牛文”的图1基本相同，只不过名字由WM和WD分别变成了高斯窗（对应于前述的高斯加权）和S窗（对应于基于Sigmoid函数的检测窗处理）。

        但是有点奇怪的是，在本文中似乎放弃了“牛文”中一个有用的技术要素：就是在检测窗中未检测到超出门限的事件但是d大于0时基于d对下一个平均窗起始位置的调整。这个技术要素对于检测性能应该是有利的。作者在后面的算法对比中采用的“原始算法”或者“旧算法”估计也是故意回避了这一技术要素。这样做的目的是为了更明显地凸显该论文的算法的advantage？But it is an unfair comparison ^-^. 

3.1 高斯加权平均

        高斯加权平均是指基于正态分布来分配权重的一种方法。用于分配权重的高斯函数如下：

 

        其中u_i表示平均窗内的每一格采样点的位置，表示平均窗中间的采样点位置。为大于0的常数，决定高斯窗的平滑程度。基于高斯加权平均方法，越靠近平均窗口中央的样点获得的权重更大。值越小，表示离中央距离越小的点获得的相对权重越大；反之则越小。趋于无限大时，高斯加权平均就退化成普通的均一权重平均了。

         实际高斯加权平均中需要对以上系数进行归一化处理，如下所示：

         当然，这个在\sigma和平均窗宽确定后高斯权重就确定了，所以以上归一化后的加权系数可以预计算，而不需要每个平均窗实时计算。

 

3.2 检测窗口的Sigmoid处理

        检测处理需要兼顾抗噪声能力和对暂态事件的敏感性，这两个要求是矛盾的，需要取折中（Trade-off）。在负荷投入（电器启动）事件发生时负荷具有持续升高的特点（不用考虑电器关断的情况吗？），逐渐放大暂态事件中持续性升到的采样值能够区分暂态事件和噪声，从而提高检测准确率。

        在检测窗口中，由于触发检测窗口的积累作用也许时由于过量的噪声因素，因此检测窗口起始阶段累计的权值比例应当降低，随着负荷水平的不断升高，逐渐提高增加的功率部分的权值，最终对爬坡事件起到放大的作用，对暂态事件进行快速识别，改进的Sigmoid函数正符合这一特性。

 图：标准的Sigmoid函数

        该论文采用的改进的Sigmoid函数如下：

 

        其中，表示检测窗口内的位置，表示检测窗口的中间位置。为大于0的常数，表示检测窗口权值的后向偏移程度，\alpha越大检测算法对于爬坡特性越敏感。=0则退化为原来的均一权重检测。与上述高斯权重一样，这里的Sigmoid权重也需要进行归一化，如下所示，同样由于它仅取决于和窗宽，可以预计算。

 

        这样基于改进Sigmoid函数的非参数化CUSUM算法中的统计函数就可以表示为：

 3.3 检测暂态过程起止位置

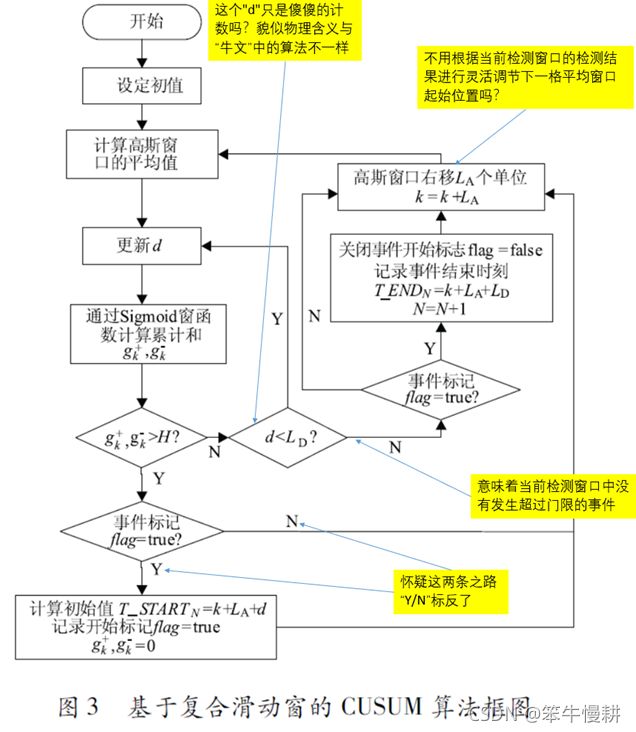
        基于复合滑动窗的CUSUM算法流程如下图所示：

        上图在细节方面存在一些疑问。但是有一点可能值得肯定，即相比“牛文”追加了如何避免一个延续事件较长的爬坡事件被重复判定为多次事件，并给出了事件起止时刻的判断。 

4. Summary

        该论文的要点如下：

1. 平均值窗口进行高斯函数处理。说的通俗一点就是，将均一权重平均该为基于高斯函数的加权平均（不妨就简称为高斯加权平均）
2. 检测窗口用改进Sigmoid函数处理，这样做可以放大爬坡过程中段信号的作用，而降低爬坡初期容易受到的噪声影响
3. 算法流程中追加了事件起止事件判断以及避免同一事件（特别是持续时间比较长的爬坡事件）被重复判定为多次事件的机制

        如上所述，论文中的描述、配图和算法流程图还存在一些疑点，需要进一步确认。

        对于高斯加权平均、检测窗的Sigmoid函数处理以及算法流程中的对于爬坡事件的避免重复判定以及事件起止时刻的判定等的效果还需要进一步考察或者通过仿真进行验证。

        但是算法流程中抛弃了“牛文”中基于当前检测窗（未检测到超过门限的事件，但是有一定积累量）的结果进行下一个平均窗起始位置的灵活调节的机制，感觉是一个减分项。而且最后的性能验证中的对比算法也似乎没有考虑这一机制，使得结果不是很客观。鉴于此，该论文的几个要点的有效性需要更进一步的检验。

 Ref: 

论文笔记：一种适用于NILM的暂态事件检测算法https://blog.csdn.net/chenxy_bwave/article/details/121145889https://blog.csdn.net/chenxy_bwave/article/details/121145889