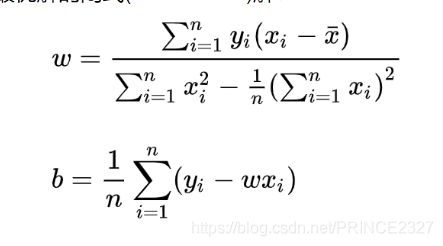机器学习——回归——一元线性回归
目录
-
- 理论部分
-
- 1.1 回归问题
- 1.2 回归问题分类
- 1.3 线性回归
- 1.4 一元线性回归
-
- 1.4.1 基本形式
- 1.4.2 损失函数
- 1.4.3 训练集与测试集
- 1.4.4 学习目标
- 1.4.5 过拟合与欠拟合
- 1.4.6 参数确定方法
-
- 1.4.6.1 解析解形式
- 1.4.6.2 梯度下降法
- 1.4.7 模型训练过程
- 代码部分
-
- 2.1 不借助sklearn实现
- 2.2 sklearn实现
理论部分
1.1 回归问题
回归与分类不同,分类的目的是区分不同样本的类别,而回归问题则是要求预测输入变量与输出变量间的关系,即研究输出关于输入的函数映射关系。回归问题的学习过程等价于拟合过程:选择一条曲线使得其能够较良好地拟合数据点的分布。
1.2 回归问题分类
回归问题依据不同的标准可以划分为不同的类别。例如,依据输入与输出之间的函数关系,可以分为线性回归与非线性回归,或者是一元回归与多元回归。依据输出变量取值的离散与连续性,可以分为离散回归与连续回归。
1.3 线性回归
线性回归指输入变量最高次数为1的回归问题。线性回归分为一元线性回归与多元线性回归。在本篇中,我们首先介绍一元线性回归,而后介绍多元线性回归。
1.4 一元线性回归
1.4.1 基本形式
一元线性回归最终学习到的映射关系有如下形式:
y ^ = ω x + b \hat{y}=\omega x+b y^=ωx+b
其中, x ∈ R , ω ∈ R , b ∈ R x \in R,\omega \in R, b \in R x∈R,ω∈R,b∈R。 ω \omega ω称为权重, b b b称为偏置, y ^ \hat{y} y^是模型的预测值。
即希望拟合一条二维直线,使得输出与输入之间的映射关系可以较为良好地被反映。
1.4.2 损失函数
为确定模型的性能好坏,我们需要一种度量模型学习情况的指标,最常见的一种度量指标被称为损失函数,它是反映模型预测标签与真实标签差异性的确定函数。在线性回归问题中,损失函数定义如下:
L = 1 n ∑ i = 1 n ( y i ^ − y i ) 2 L=\frac{1}{n} \sum_{i=1}^{n} (\hat{y_{i}}-y_{i})^{2} L=n1i=1∑n(yi^−yi)2
其中: n n n为样本总数, y ^ \hat{y} y^为模型预测标签, y y y为样本真实标签。上面这种损失函数称为均方损失函数或 L 2 L2 L2损失函数。
可以看出: y ^ − y \hat{y}-y y^−y代表了模型预测标签与样本真实标签的差异性,而对它们的平方一方面是为了防止正负偏差抵消,另一方面也是为了保证损失函数为凸函数(这样可以保证模型收敛到最优情况), 1 n \frac{1}{n} n1是平均了所有误差,得到所有样本的平均误差,平滑极端值的影响。
1.4.3 训练集与测试集
通常在机器学习中,可以简单地将样本集划分为训练集与测试集,两者比例大约为 7 : 3 7:3 7:3。训练集用于模型的训练,即通过模型对于训练集样本的学习去调整自身的参数情况,从而达到最优。而测试集则是用于对训练好的模型进行测试,当模型训练完成后,我们需要了解该模型在新数据集上(这里的新数据集指除去训练集的那部分数据集)的表现,以此来推断模型在新数据集上的推广能力(这称为泛化能力)。
1.4.4 学习目标
线性回归模型的学习目标是使得损失函数 L L L达到最小或足够小的次小,损失函数的降低标志着模型预测标签与真实标签的接近,也即模型在训练数据集上表现优良。
通常来说,我们所指的损失函数达到最小指的应为在新数据集上的最小(即标志着训练完成的模型有较好的泛化能力),但这往往是较困难的,模型训练时我们并不能确切知道它在新样本上的应用能力。基于此,训练模型时的目标变为了在训练集上使损失函数达到最小。
1.4.5 过拟合与欠拟合
在一定程度上,训练集上损失函数的降低可以代表测试集上损失函数的降低,也即标志着模型的性能提升。但在“过度学习后”,两者往往并不等价,一个例子如下:
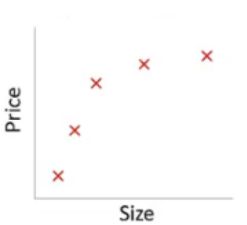
我们需要根据上图中的样本点得到一条拟合曲线,现有以下三种结果:

但从训练集的损失函数来看,似乎图1为最佳情况(因为它在训练集上的损失为0)。但在测试样本上,图1的表现往往不尽人意。这是因为,图1所代表的模型“过度学习了”训练数据集,以至于包含在其中的噪声也被模型所学习,这导致模型在训练集上表现良好,但却在测试集上表现较差,这种现象称为过拟合,过拟合的模型复杂度往往很高。
图3所对应的情况称为欠拟合,模型在训练集上的损失函数尚且未到较优值,尚且“缺乏学习”,在测试集上自然也不会有较好的效果。欠拟合的情况往往在训练集和测试集上表现都较差,欠拟合的模型复杂度往往很低。
图2是模型训练的理想情况,在这种情况下,模型即学习到了数据中的主要特征,又忽略了噪声所带来的影响,即学到了真正影响输出的因素,这种情况往往在测试集上有较好的性能,能够推广在新数据集上使用,其模型复杂度介于欠拟合情况与过拟合情况之间。
1.4.6 参数确定方法
关于线性回归模型如何学习样本数据,从而得到自身的较优参数,一般有两种方法:
1.4.6.1 解析解形式
解析解形式即采用纯粹的数学方法去解出最优情况下的权重 ω \omega ω和偏置 b b b:
损失函数可改写为如下形式:

分别对权重和偏置求偏导数,得到如下结果:
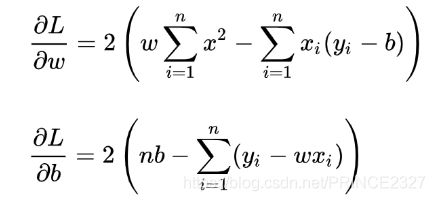
1.4.6.2 梯度下降法
上述方法可以解决线性回归问题,但在机器学习中,我们更多地需要模型去“自主学习”,而不是人为地指定。所以我们常用的方法是一种称为梯度下降法的优化方法。
梯度下降法是机器学习与深度学习中最常使用到的优化算法,也是后续算法的基石。下面以多维梯度下降法为例简述其原理:
假设对于损失函数 L ( x ) L(x) L(x),其输入 x = [ x 1 , x 2 , x 3 , . . . . . . , x n ] T x=[x_{1},x_{2},x_{3},......,x_{n} ]^{T} x=[x1,x2,x3,......,xn]T是一个n维向量,其输入为标量(即一个实数)。
则损失函数的梯度可表示为: ▽ L ( x ) = [ ∂ f ( x ) ∂ x 1 , ∂ f ( x ) ∂ x 2 , ∂ f ( x ) ∂ x 3 , . . . . . . , ∂ f ( x ) ∂ x n ] T \bigtriangledown L(x)=[\frac{\partial f(x)}{\partial x_{1}},\frac{\partial f(x)}{\partial x_{2}},\frac{\partial f(x)}{\partial x_{3}},......,\frac{\partial f(x)}{\partial x_{n}}]^{T} ▽L(x)=[∂x1∂f(x),∂x2∂f(x),∂x3∂f(x),......,∂xn∂f(x)]T
其中 ∂ L ( x ) ∂ x i \frac{\partial L(x)}{\partial x_{i}} ∂xi∂L(x)表示损失函数关于样本 x x x中特征 x i x_{i} xi的变化率。
依据方向导数性质, L ( x ) L(x) L(x)在某一方向 u u u上的变化率 D u f ( x ) D_{u}f(x) Duf(x)为:
D u L ( x ) = ▽ L ( x ) ⋅ u = ▽ L ( x ) c o s ( θ ) ∣ ∣ u ∣ ∣ D_{u}L(x)=\bigtriangledown L(x)·u=\bigtriangledown L(x)cos(\theta)||u|| DuL(x)=▽L(x)⋅u=▽L(x)cos(θ)∣∣u∣∣
为了尽快降低损失,我们需要该方向导数尽可能的为足够小的负数,从而当损失函数沿着该方向移动时,能够保证其下降最快。根据上式明显可以看出:当 θ = π \theta=\pi θ=π时,方向导数值最小,下降最快。故有:
x = x − α ▽ L ( x ) x=x-\alpha \bigtriangledown L(x) x=x−α▽L(x)
这就是批量梯度下降法的公式。其中 α \alpha α称为学习率,它控制着每一步步长的相对大小。
考虑如上图的一个函数(横坐标为 ω \omega ω,纵坐标为损失值),假设初始时损失值位于左侧较高点。此时损失函数对于 ω \omega ω求梯度为负值,所以 ω = ω − α ∂ L ( x ) ∂ ω \omega=\omega - \alpha\frac{\partial L(x)}{\partial \omega} ω=ω−α∂ω∂L(x)
会使得 ω \omega ω变大,根据上图, ω \omega ω变大会使得损失更靠近最低点,从而降低损失。如果此时损失点位于最低点左侧,也可以根据此原理来向最低点靠近。
这里学习率 α \alpha α控制了每一次梯度下降参数变化的幅度
当学习率过小时,更新速度较慢,此时需要更多迭代周期和更长时间。
当学习率过大时,步长较长,有可能从最低点的左侧一步跨至最低点的右侧,造成损失函数的振荡行为,从而无法收敛。
1.4.7 模型训练过程
线性回归模型的训练过程,就是在每次学习样本后使用梯度下降法对权重和偏置参数进行更新,直到达到最优或较优情况。
代码部分
2.1 不借助sklearn实现
这是一个预测人口数量与超市利润关系的例子:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
def load_data(path):
data=pd.read_csv(path,header=None,names=['population','profit'])
return data ,data.head(),data.describe()
data,data_head,data_describe=load_data('ex1data1.txt')
#print(type(data))
#print(data_head)
#print(data_describe)
def visualization_data():
fig,ax=plt.subplots(figsize=(6,6))
ax.scatter(data['population'],data['profit'])
ax.set_xlabel('population')
ax.set_ylabel('profit')
ax.set_title('population vs profit')
plt.show()
#visualization_data()
def data_preprocessing():
data.insert(0,'one',1)
col=data.shape[1]
x=data.iloc[:,:col-1]
y=data.iloc[:,col-1:]
return x,y
x,y=data_preprocessing()
x=np.array(x.values)
y=np.array(y.values)
#print('x:',x)
#print('y:',y)
theta=np.array([[0,0]])
print('x:',x.shape,'y:',y.shape,'theta',theta.shape)
def costfunction(x,y,theta):
h=x@theta.T
temp=np.power((h-y),2)
J=np.sum(temp)/(2*len(x))
return J
J=costfunction(x,y,theta)
#print(J)
def gradientdescend(x,y,theta,alpha,num_iter):
theta_t=np.array(np.zeros(theta.shape))
cost=np.zeros(num_iter)
m=len(x)
for i in range(num_iter):
theta_t=theta-(alpha/m)*(x@theta.T-y).T@x
theta=theta_t
cost[i]=costfunction(x,y,theta)
return theta,cost
alpha=0.01
iterations=1000
fin_theta,cost=gradientdescend(x,y,theta,alpha,iterations)
fin_cost=costfunction(x,y,fin_theta)
print('fin_cost',fin_cost)
print('fin_theta:',fin_theta,fin_theta.shape)
x=np.linspace(data.population.min(),data.population.max(),200)
f=fin_theta[0,0]+(fin_theta[0,1]*x)
fig,ax=plt.subplots(figsize=(8,8))
ax.plot(x,f,'black',label='result of prediction')
ax.scatter(data['population'],data['profit'])
ax.set_xlabel('population')
ax.set_ylabel('profit')
ax.set_title('population VS profit')
plt.show()
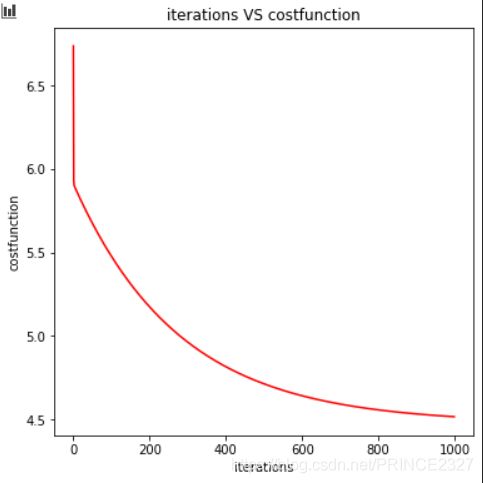
fig,ax=plt.subplots(figsize=(6,6))
ax.plot(np.arange(iterations),cost,'r')
ax.set_xlabel('iterations')
ax.set_ylabel('costfunction')
ax.set_title('iterations VS costfunction')
plt.show()
可以看到,损失函数的明显下降。
2.2 sklearn实现
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
# Load the diabetes dataset
diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y=True)
# Use only one feature
diabetes_X = diabetes_X[:, np.newaxis, 2]
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
# Split the targets into training/testing sets
diabetes_y_train = diabetes_y[:-20]
diabetes_y_test = diabetes_y[-20:]
# Create linear regression object
regr = linear_model.LinearRegression()
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print('Mean squared error: %.2f'
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# The coefficient of determination: 1 is perfect prediction
print('Coefficient of determination: %.2f'
% r2_score(diabetes_y_test, diabetes_y_pred))
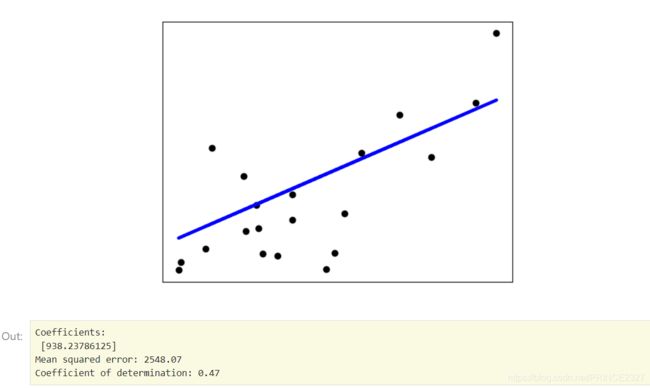
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
欢迎交流。