机器学习——线性回归(Linear Regression)(吴恩达机器学习)
机器学习——线性回归(Linear Regression)
- 房屋价格预测
- 监督学习过程
- 线性回归模型
- 求解代价函数最小化问题——梯度下降(Gradient descent)
-
- 梯度下降算法思路
- 梯度下降算法数学定义
- 线性回归梯度下降算法
房屋价格预测

在监督学习里,我们有一个数据集,它被称为一个训练集
一些符号:
m:训练样本的数量
x:输入变量/特征
y:输出变量/目标变量
(x,y):表示一个训练样本
(x(i),y(i)):第i个训练样本
监督学习过程
1.我们向学习算法提供训练集
2.学习算法的任务是输出一个函数,,通常用小写h表示,h代表假设函数(hypothesis),假设函数的作用是,输入x值,输出预测的y值
3.下一个要考虑的问题是如何表示这个假设函数h?
一种形式是 h ( x ) = a x + b h(x) = ax + b h(x)=ax+b,即y是x的线性函数,这就被称为线性回归,由于只有一个自变量x,所以称为一元线性回归或者单变量线性回归(Univariate linear regression)

线性回归模型
我们要做的就是得出a和b的值,来让假设函数表示的直线尽量地与这些数据点很好的拟合

在标准定义中,线性回归我们要解决一个最小化问题,即让预测的h(x)值和准确的y值的误差尽可能的小,即让误差的平方和最小,数学公式表示为:
m i n i m i z e a , b ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 ( m 表 示 训 练 样 本 的 数 量 ) minimize_{a,b} \displaystyle\sum_{i=1}^{m}(h(x^{(i)}) - y^{(i)})^2\qquad (m表示训练样本的数量) minimizea,bi=1∑m(h(x(i))−y(i))2(m表示训练样本的数量)
或者
m i n i m i z e a , b 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 ( m 表 示 训 练 样 本 的 数 量 ) minimize_{a,b}\quad \frac{1}{2m}\displaystyle\sum_{i=1}^{m}(h(x^{(i)}) - y^{(i)})^2\qquad (m表示训练样本的数量) minimizea,b2m1i=1∑m(h(x(i))−y(i))2(m表示训练样本的数量)
定义代价函数(cost function)
J ( a , b ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 ( m 表 示 训 练 样 本 的 数 量 ) J(a,b)= \frac{1}{2m}\displaystyle\sum_{i=1}^{m}(h(x^{(i)}) - y^{(i)})^2\qquad (m表示训练样本的数量) J(a,b)=2m1i=1∑m(h(x(i))−y(i))2(m表示训练样本的数量)
代价函数也被称为平方误差函数或者平方误差代价函数,在线性回归问题中,平方误差函数是最常用的手段。

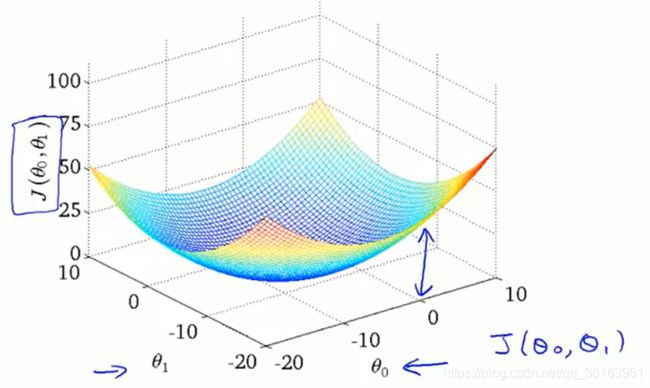
图中 θ 0 \theta_0 θ0对应b, θ 1 \theta_1 θ1对应a
在实际中,需要求解的参数可能不止两个,可能有n个: θ 0 , θ 1 , θ 2 . . . θ n \theta_0,\theta_1,\theta_2...\theta_n θ0,θ1,θ2...θn。
代价函数其实是关于a和b的二次函数,所以代价函数关于a和b的变化曲线就是碗状的
求解代价函数最小化问题——梯度下降(Gradient descent)
梯度下降算法思路
1.Start with some θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1,即我们指定 θ 0 和 θ 1 \theta_0和\theta_1 θ0和θ1的初始值,比如可以让他们都为0
2.Keep changing θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1 to reduce J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1),不断改变 θ 0 和 θ 1 \theta_0和\theta_1 θ0和θ1的值,使 J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)不断减小
3.Until we hopefully end up at a minimum.直到我们得到一个最小值或者局部最小值
梯度的概念:函数中某一点 ( x , y ) (x,y) (x,y)的梯度代表函数在该点变化最快的方向,对于有两个自变量 x , y x,y x,y的函数来说,梯度是一个二维向量。
在下面图中,我们从一个点开始,不断寻找所在点的梯度,并沿梯度方向移动一小段距离,最后会到达一个局部最小值;

然而如果我们选择另一个点开始算法,则有可能到达另一个不同的局部最小值。这是梯度下降算法的一个特点。

梯度下降算法数学定义
重复执行下面的式子,直到到达一个局部最小值
θ j : = θ j − α ∂ J ( θ 0 , θ 1 ) ∂ θ j ( j = 0 , 1 ) \theta_j := \theta_j - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_j}\qquad (j=0,1) θj:=θj−α∂θj∂J(θ0,θ1)(j=0,1)
其中 : = := :=表示赋值, α \alpha α是学习率(Learning Rate),它控制我们以多大的幅度更新参数 θ j \theta_j θj, α \alpha α越大,算法就会更快地到达局部最小值。
需要注意的是, θ 0 和 θ 1 \theta_0和\theta_1 θ0和θ1是同步更新的,正确的顺序:
t e m p 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 0 temp0 := \theta_0 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} temp0:=θ0−α∂θ0∂J(θ0,θ1)
t e m p 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 temp1 := \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 0 : = t e m p 0 \theta_0 := temp0 θ0:=temp0
θ 1 : = t e m p 1 \theta_1 := temp1 θ1:=temp1
错误的顺序:
t e m p 0 : = θ 0 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 0 temp0 := \theta_0 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_0} temp0:=θ0−α∂θ0∂J(θ0,θ1)
θ 0 : = t e m p 0 \theta_0 := temp0 θ0:=temp0
t e m p 1 : = θ 1 − α ∂ J ( θ 0 , θ 1 ) ∂ θ 1 temp1 := \theta_1 - \alpha \frac{\partial J(\theta_0,\theta_1)}{\partial \theta_1} temp1:=θ1−α∂θ1∂J(θ0,θ1)
θ 1 : = t e m p 1 \theta_1 := temp1 θ1:=temp1
错误的顺序在计算 t e m p 1 temp1 temp1时,已经更新了 θ 0 \theta_0 θ0, t e m p 1 temp1 temp1的值会产生微小的差别,此时的算法不再是梯度下降算法。
假设只有一个参数 θ 1 \theta_1 θ1的情形

考虑 α \alpha α大小问题, α \alpha α很小时,每次只移动一小步,最终到最小值收敛,算法结束,但是如果 α \alpha α很大,每次移动一大步,可能会越过最小值,最终不会收敛甚至会发散

考虑 θ 1 \theta_1 θ1位于局部最小值时的场景,此时导数为0, θ 1 \theta_1 θ1不再变化,这是为什么即使 α \alpha α是固定值,算法最终也能收敛到局部最小值的原因,在逐渐接近局部最小值的过程中,导数逐渐减小,每一步的步幅也会越来越小,所以不需要随着时间变化而改变 α \alpha α值,当然 α \alpha α太大是不行的

线性回归梯度下降算法

J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h ( x ( i ) ) − y ( i ) ) 2 J(\theta_0,\theta_1) = \frac{1}{2m}\displaystyle\sum_{i=1}^{m}(h(x^{(i)})- y^{(i)})^2 J(θ0,θ1)=2m1i=1∑m(h(x(i))−y(i))2
= 1 2 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) ) − y ( i ) ) 2 \qquad\qquad= \frac{1}{2m}\displaystyle\sum_{i=1}^{m}((\theta_0 + \theta_1x^{(i)}) - y^{(i)})^2 =2m1i=1∑m((θ0+θ1x(i))−y(i))2
偏导数:
∂ J ( θ 0 , θ 1 ) ∂ θ 0 = 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) ) − y ( i ) ) \frac{\partial{J(\theta_0,\theta_1) }}{\partial \theta_0} = \frac{1}{m}\displaystyle\sum_{i=1}^{m}((\theta_0 + \theta_1x^{(i)}) - y^{(i)}) ∂θ0∂J(θ0,θ1)=m1i=1∑m((θ0+θ1x(i))−y(i))
∂ J ( θ 0 , θ 1 ) ∂ θ 1 = 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) ) − y ( i ) ) x ( i ) \frac{\partial{J(\theta_0,\theta_1) }}{\partial \theta_1} = \frac{1}{m}\displaystyle\sum_{i=1}^{m}((\theta_0 + \theta_1x^{(i)}) - y^{(i)}) x^{(i)} ∂θ1∂J(θ0,θ1)=m1i=1∑m((θ0+θ1x(i))−y(i))x(i)
每一步更新如下:
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) ) − y ( i ) ) \theta_0 := \theta_0 - \alpha \frac{1}{m}\displaystyle\sum_{i=1}^{m}((\theta_0 + \theta_1x^{(i)}) - y^{(i)}) θ0:=θ0−αm1i=1∑m((θ0+θ1x(i))−y(i))
θ 1 : = θ 1 − α 1 m ∑ i = 1 m ( ( θ 0 + θ 1 x ( i ) ) − y ( i ) ) x ( i ) \theta_1 := \theta_1 - \alpha \frac{1}{m}\displaystyle\sum_{i=1}^{m}((\theta_0 + \theta_1x^{(i)}) - y^{(i)}) x^{(i)} θ1:=θ1−αm1i=1∑m((θ0+θ1x(i))−y(i))x(i)
对于线性回归, J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1)只有一个最小值,所以梯度下降算法最后收敛到这个最小值
这个梯度下降算法又叫“Batch”梯度下降算法,“Batch”意味着在每一步中都使用了所有的训练样本。
后面会讲到正规方程组方法(normal equations methods)求解最小值问题,它不需要多步骤梯度下降,但是梯度下降算法可以用于更大的数据集。
