线性回归liner regression
线性回归 liner regression
-
- 模型描述
-
- 回归分析
- 线性回归
- 部分预备知识
- 假设函数(hypothesis)
- 损失函数/代价函数(cost/loss function)
- 等高线图(contour figure)
- 批量梯度下降(Batch Gradient Descent)
- 随机梯度下降(Stochastic Graident Descent)
- 正规方程(Nomal Equation)
- 特征缩放
- 多项式回归
- 欠拟合和过拟合
-
- 局部加权线性回归
- 正规化
模型描述
回归分析
回归分析(regression)是一种预测分析技术,探讨的是因变量(目标)和自变量(预测器)之间的关系。通常使用直线或是曲线来拟合数据点,目的是使曲线到数据点的距离差异最小。
线性回归
线性回归(liner regression)是回归问题中的一种,它假设目标值与参数(即特征)之间线性相关,满足一元一次方程,假设损失函数,通过使损失函数最小计算合适的一元一次方程的系数。
部分预备知识
一个样本空间的数据为了方便和提高性能,通常会被分为训练集(training set)、交叉验证集(cross vadidation set)和测试集(test set)。自己的理解:训练集用来训练产生模型,交叉验证集用来调整模型以达到最佳的效果,测试集用来评估模型的性能(刚入门,可能理解有误,后序有误会回过来调整)。
对于学习,重要的有两件事情:
- 对学习的正确性和性能,我们能有指标去衡量;
- 当学习情况不佳时,我们能有手段去纠正它。
特征(feature): x i x_i xi,下标 i i i是指第 i i i个特征,例如判断好西瓜中的颜色、大小、声音,都可以作为学习的特征;
输入: x x x,也被称为特征向量,由一个样本的特征值组成, x j ( i ) x_j^{(i)} xj(i)指的是第i个特征向量(样本)中的第 j j j个特征;
输出:输出向量 y y y, y ( i ) y^{(i)} y(i)指的是对于第 i i i个输入对应的输出。
假设函数(hypothesis)
h y p o t h e s i s hypothesis hypothesis—假设函数通常表示为小写的h或者 h θ ( x ) h_\theta(x) hθ(x)表示,这个是用于预测输出的函数,取名hypothesis只是习惯问题,不用深究命名。一般如下表示: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n = θ T x h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n=\theta^Tx hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn=θTx 机器学习的关键就是通过损失函数求的最优的 θ \theta θ系数以及假设函数,也就是模型,从而对于未训练过的数据表现出良好的泛化能力。
损失函数/代价函数(cost/loss function)
损失函数,也称代价函数,用于在机器学习中做误差评估,评估预测值 h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i))与实际值 y ( i ) y^{(i)} y(i)之间的误差,通常采用最小均方(least mean square)来描述: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2其中 m m m表示样本数量。
矩阵表达: J ( θ ) = 1 2 m ( X θ − y ) T ( X θ − y ) J(\theta)=\frac{1}{2m}(X\theta-y)^T(X\theta-y) J(θ)=2m1(Xθ−y)T(Xθ−y)调整参数 θ \theta θ的目的就是求 m i n i m i z e ( J ( θ ) ) minimize(J(\theta)) minimize(J(θ))。
等高线图(contour figure)
课程中举例的 J ( θ ) J(\theta) J(θ)图像是一个三维的图像,使用等高线图去将三维的图像反应在二维图像中,就像地理中使用的等高线图一样,同一条等高线上的 J ( θ ) J(\theta) J(θ)相等。
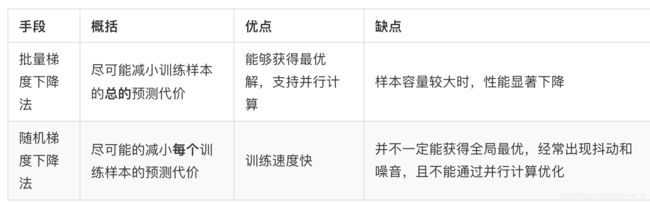
批量梯度下降(Batch Gradient Descent)
梯度下降和正规方程是用于纠正学习情况不佳(也就是代价函数过大)的主要方法。
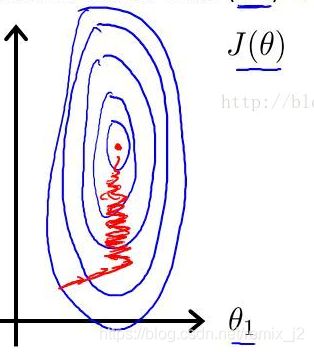
调整的过程就是不断调整参数 θ \theta θ去使损失函数足够小,通常定义小于一个值后就达到所需要的精度。 θ j = θ j − α ∂ ∂ θ j J ( θ ) \theta_j=\theta_j-\alpha\frac{\partial}{\partial \theta_j}J(\theta) θj=θj−α∂θj∂J(θ) α \alpha α在这里指学习率,可以表示为沿梯度方向下降的速率,结合图像可以把它想象成买下一步的步长,在实际使用中要选择合适的大小,可以3倍变化着取值,例如 α = 0.001 , 0.003 , 0.01 , 0.03 , ⋯ , 1 \alpha=0.001,0.003,0.01,0.03,\cdots,1 α=0.001,0.003,0.01,0.03,⋯,1 梯度方向是一个函数下降的最快的方向,所以在调整过程中,我们尽可能沿着最快下降方向前进,这样才能接近局部最优解,也就是 J ( θ ) J(\theta) J(θ)局部最小值,因为这里举例的是线性回归,它的函数是一个凸函数,局部最优点也就是整体最优点。举个例子,就像是下山,我们想要尽快到达山底,所以我们会沿着最倾斜的坡下山。
梯度下降过程中,我们会迭代进行上面的式子,直至整个函数收敛。需要注意的是,所有 θ j \theta_j θj同步更新,要求互相监督。而非更新了一个参数后,将这个参数代入计算另一个参数。
在局部最优点时,梯度下降法实际上什么也没有做,停止更新了,因为偏导数等于0,参数不再更新。在不断接近最优点的过程中,梯度下降算法会不断调整控制步长的a,不断的去试探,尝试到达局部最优点。实际使用中,随着逐渐逼近最优点,导数值会不断降低,所以并没有必要去不断减小a值。(这边理解有点问题)
缺点:每更新一个参数,都需要遍历一遍样本,所以当样本数m很大时,效率不高。解决的一个办法是用向量表示,利用并行计算优化性能。当然,还可以采用以下提到的随机梯度下降。
随机梯度下降(Stochastic Graident Descent)
过程如下
重复直至收敛(repeat until convergence)
for i =1 to m: θ j = θ j + α ( y ( i ) − h θ ( x ( i ) ) ) x j ( i ) \theta_j=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)} θj=θj+α(y(i)−hθ(x(i)))xj(i) 在随机梯度下降算法中,没更新一个 θ j \theta_j θj只需要一个样本,所以即使样本数很大,也不影响性能。
正规方程(Nomal Equation)
通过使用正规方程,可以避免梯度下降中要不断调节学习率 α \alpha α的问题。 θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy 其中, X X X表示输入向量矩阵, y y y表示目标向量。
这些的计算特别方便,无论哪种语言,都提供了许多优秀的第三方库可调用用于计算。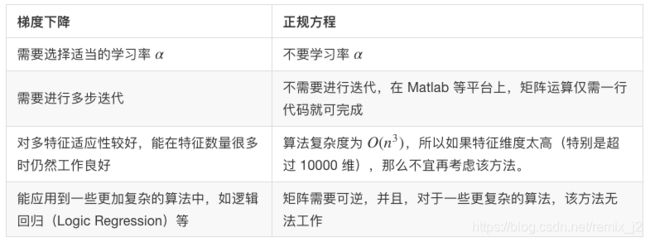
本质上是将问题划为了线性代数进行处理,通过矩阵计算找出合适的参数。
与梯度下降法的区别(对于n特征,m个训练样本的训练集):
梯度下降:
1、需要选择合适的学习率;
2、多次迭代;
3、当n较大时,表现良好;
4、能应用在诸如逻辑回归等一些更加复杂的算法中。
正规方程:
1、不需要学习率;
2、不用迭代计算,实现简单;
3、算法时间复杂度为O(n^3),不适用于n较大的情况,因为计算复杂;
4、矩阵需要可逆,非奇异矩阵,适用情况不及梯度下降。
当遇到计算的矩阵不可逆,为奇异矩阵时,建议两种处理方式:
1、删除多余的特征,观察是否存在线性相关的特征值,有的话删除多余的;
2、存在很多特征时,观察是否可以删除某些影响不大的特征,或者使用正规化(之后会讨论)。
特征缩放
是梯度下降方法中的小技巧。实际上是归一化,使特征参数的数值缩小在较小的值范围之间,本质上是想将各种特征量化到统一的区间,加快收敛。
两种量化方式:
1)Standardization,又称为Z-score normalization,量化后的特征将服从标准正态分布: z = x i − μ δ z=\frac{x_i-\mu}{\delta} z=δxi−μ μ \mu μ, δ \delta δ分别代表 x i x_i xi的均值和标准差。量化后的特征分布将在[-1,1]之间.
2)Min-Max Scaling
又称normalization z = x i − m i n ( x i ) m a x ( x i ) − m i n ( x i ) z=\frac{x_i-min(x_i)}{max(x_i)-min(x_i)} z=max(xi)−min(xi)xi−min(xi)量化后的特征将在[0,1]之间,视频中主要讲解的是这种。
经过特征缩放后图像将会由“扁长”变为“均匀”。

多项式回归
如何将一个二次方程或一个三次方程拟合到数据上:选择合适的特征,例如长和高两个特征值可以结合为土地的面积这一个特征。
并且可以在方程中添加高阶项,来提高拟合效果。
欠拟合和过拟合
欠拟合(underfitting):拟合程度不高,存在bias偏差,就是样本数据离拟合的曲线偏差较大;
过拟合(underfitting):曲线能够拟合训练样本中的每个数据,但是因此难以发现训练数据中的普遍规律,泛化能力差。
局部加权线性回归
解决方法:引入局部加权线性回归(Locally Weight Regresiion)。

对 x x x进行预测时,对x周围的点赋予不同的权值,离x越近,权值越高。权值越高,那么这个样本的结果对假设函数的参数(更进一步的,预测结果)影响越大。整个过程的误差取决于x周围的误差,而非整体样本的误差,所以这一方法带有“局部”的特性。
通常, w ( i ) w^(i) w(i)服从高斯分布,在 x x x的周围呈指数衰减: w ( i ) = e − ( x ( i ) − x ) 2 2 τ 2 w^(i)=e^{-\frac{(x^{(i)}-x)^2}{2\tau^2}} w(i)=e−2τ2(x(i)−x)2 τ \tau τ越小,越靠近,权值越大,影响越大。
正规化
正规化是解决线性回归过拟合问题更常见的方法。
1)减少特征数
2)平滑曲线
我们主要要做的就是弱化高阶项系数对假设函数的影响,这样可以减弱曲线的曲折度,我们可以给代价函数加入一个惩罚项(penalize)。
注意我们惩罚项的下标是从1开始,因为 θ 0 \theta_0 θ0是我们给定的一个常数,对代价函数影响不大。
λ \lambda λ特别大,则惩罚项的权重越大,要使代价函数尽可能小,则 θ \theta θ会特别小,有可能出现偏差。
λ \lambda λ特别小,则可能出现过拟合现象。
这里可以结合到后面SVM支持向量机一章,代价函数的形式有一些不一样,但是它没有了 λ \lambda λ,而是在第一项的前面带上常数 C C C,作用其实可以示做 1 λ \frac{1}{\lambda} λ1, C C C越大,过拟合;越小,出现偏差。这也是为什么SVM被叫做最大间距分类器,总是选择离决策边界(decision boundary)最近样本拥有最大间距(margin)的决策边界的原因。
参考部分:https://www.cnblogs.com/geo-will/p/10306691.html