剑指Offer---2021/7/18
目录
- 剑指 Offer 10- I. 斐波那契数列
- 剑指 Offer 10- II. 青蛙跳台阶问题
- 剑指 Offer 11. 旋转数组的最小数字
- 剑指 Offer 05. 替换空格
- 剑指 Offer 06. 从尾到头打印链表
- 剑指 Offer 25. 合并两个排序的链表
- 剑指 Offer 27. 二叉树的镜像
- 剑指 Offer 28. 对称的二叉树
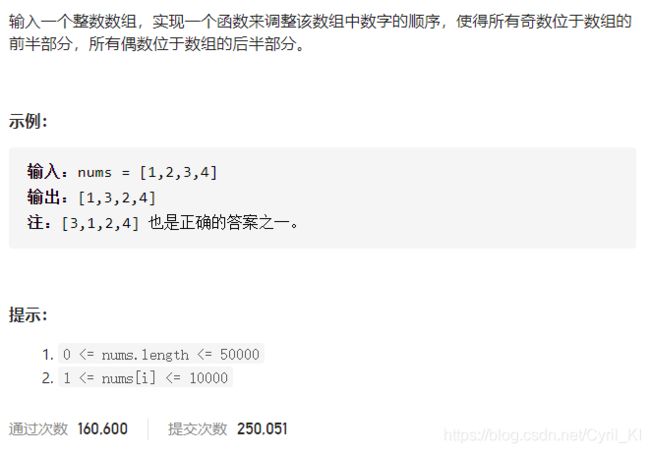
- 剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
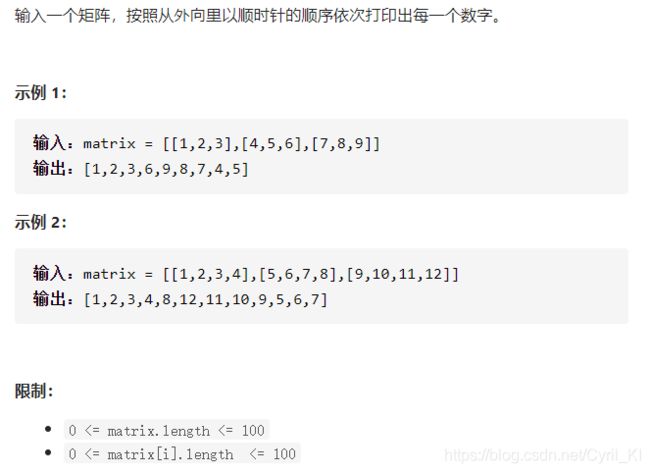
- 剑指 Offer 29. 顺时针打印矩阵
- 剑指 Offer 22. 链表中倒数第k个节点
- 剑指 Offer 17. 打印从1到最大的n位数
- 剑指 Offer 24. 反转链表
- 剑指 Offer 18. 删除链表的节点
- 剑指 Offer 40. 最小的k个数
- 剑指 Offer 30. 包含min函数的栈
- 剑指 Offer 42. 连续子数组的最大和
- 剑指 Offer 39. 数组中出现次数超过一半的数字
剑指 Offer 10- I. 斐波那契数列

分析:
(x + y) % mod = (x % mod + y % mod) % mod。
代码:
class Solution {
public:
int fib(int n) {
const long long int mod = 1e9 + 7;
long long x = 0, y = 1;
int z = 0;
if(n == 0) {
return 0;
}
if(n == 1 || n == 2) {
return 1;
}
for(int i = 2; i <= n; i++) {
z = (x % mod + y % mod) % mod;
x = y;
y = z;
}
return z % mod;
}
};
剑指 Offer 10- II. 青蛙跳台阶问题

分析:
f(i) = f(i - 1) + f(i - 2)。
代码:
class Solution {
public:
int numWays(int n) {
const long long mod = 1e9 + 7;
int x = 1, y = 2;
int z = 0;
if(n == 0 || n == 1) {
return 1;
}
if(n == 2) {
return 2;
}
for(int i = 3; i <= n; i++) {
z = (x % mod + y % mod) % mod;
x = y, y = z;
}
return z % mod;
}
};
剑指 Offer 11. 旋转数组的最小数字
class Solution {
public:
int minArray(vector<int>& numbers) {
return *min_element(numbers.begin(), numbers.end());
}
};
方法二:
二分查找,参考官方题解。
代码:
class Solution {
public:
int minArray(vector<int>& numbers) {
int low = 0;
int high = numbers.size() - 1;
while (low < high) {
int pivot = low + (high - low) / 2;
if (numbers[pivot] < numbers[high]) {
high = pivot;
}
else if (numbers[pivot] > numbers[high]) {
low = pivot + 1;
}
else {
high -= 1;
}
}
return numbers[low];
}
};
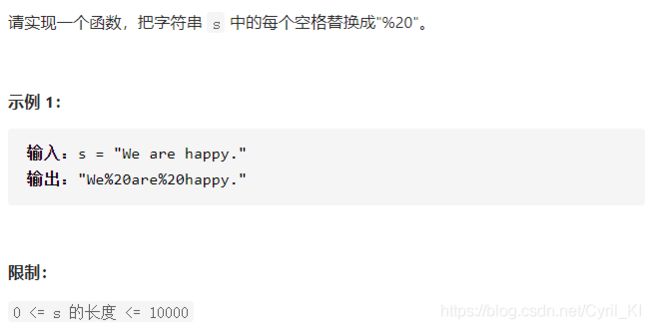
剑指 Offer 05. 替换空格
分析:
使用O(n)的额外空间定义一个字符串,遍历原字符串,遇到空格就替换。
代码:
class Solution {
public:
string replaceSpace(string s) {
string rep = "%20";
string res = "";
for(int i = 0; i < s.size(); i++) {
if(s[i] == ' ') {
res += rep;
}else {
res += s[i];
}
}
return res;
}
};
剑指 Offer 06. 从尾到头打印链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
vector<int> res;
while(head) {
res.push_back(head->val);
head = head->next;
}
reverse(res.begin(), res.end());
return res;
}
};
方法二:
利用栈保存遍历链表时访问的元素,然后顺序输出栈中的元素。
代码:
较为简单,不再编写。
剑指 Offer 25. 合并两个排序的链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode* prev = new ListNode(0);
ListNode* head = prev;
if(l1 == NULL) {
return l2;
}
if(l2 == NULL) {
return l1;
}
while(l1 && l2) {
int x1 = l1->val, x2 = l2->val;
if(x1 <= x2) {
prev->next = l1;
l1 = l1->next;
}else {
prev->next = l2;
l2 = l2->next;
}
prev = prev->next;
}
prev->next = l1 == NULL ? l2 : l1;
return head->next;
}
};
剑指 Offer 27. 二叉树的镜像

分析:
递归,递归太难,参考官方理解:从根节点开始,递归地对树进行遍历,并从叶子节点先开始翻转得到镜像。如果当前遍历到的节点root的左右两棵子树都已经翻转得到镜像,那么我们只需要交换两棵子树的位置,即可得到以root为根节点的整棵子树的镜像。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* mirrorTree(TreeNode* root) {
if (root == nullptr) {
return nullptr;
}
TreeNode* left = mirrorTree(root->left);
TreeNode* right = mirrorTree(root->right);
root->left = right;
root->right = left;
return root;
}
};
剑指 Offer 28. 对称的二叉树

分析:
很容易想到的方法是先得到树的镜像树,然后判断二者是否相同。不过这里也可以采用递归,见代码注释。
代码:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
bool isSymmetric(TreeNode* root) {
// 空树
if(!root)
return true;
else
return isSymmetric(root->left, root->right);
}
// 此函数比较二叉树中位置对称的两个节点
bool isSymmetric(TreeNode* left, TreeNode* right){
// 结束条件1:如果对称两个节点都为空,则返回true
if(!left && !right){
return true;
}
// 结束条件2:如果单独一个节点为空,另一个节点不为空,又或者是对称节点间的val值不等,则返回false
if(!left || !right || left->val != right->val)
return false;
// 该层符合对称二叉树的要求,开始比较下一层
return isSymmetric(left->left, right->right) && isSymmetric(left->right, right->left);
}
};
剑指 Offer 21. 调整数组顺序使奇数位于偶数前面
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
vector<int> res1, res2;
if(nums.size() == 0) {
return res1;
}
for(int i = 0; i < nums.size(); i++) {
if(nums[i] & 1) {
res1.push_back(nums[i]);
}else {
res2.push_back(nums[i]);
}
}
for(int i = 0; i < res2.size(); i++) {
res1.push_back(res2[i]);
}
return res1;
}
};
class Solution {
public:
vector<int> exchange(vector<int>& nums) {
int left = 0, right = nums.size() - 1;
while (left < right) {
if ((nums[left] & 1) != 0) {
left ++;
continue;
}
if ((nums[right] & 1) != 1) {
right --;
continue;
}
swap(nums[left++], nums[right--]);
}
return nums;
}
};
剑指 Offer 29. 顺时针打印矩阵
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
if(matrix.empty()) {
return res;
}
int m = matrix.size(), n = matrix[0].size();
vector<vector<int>> vis(m, vector<int>(n, 0));
int cnt = 0, x = 0, y = 0;
while(cnt < m * n) {
//右
while(y < n && !vis[x][y]) {
res.push_back(matrix[x][y]);
vis[x][y] = 1;
cnt++;
y++;
}
//下
y--, x++;
while(x < m && !vis[x][y]) {
res.push_back(matrix[x][y]);
vis[x][y] = 1;
cnt++;
x++;
}
//左
x--, y--;
while(y >= 0 && !vis[x][y]) {
res.push_back(matrix[x][y]);
vis[x][y] = 1;
cnt++;
y--;
}
//上
x--, y++;
while(x >= 0 && !vis[x][y]) {
res.push_back(matrix[x][y]);
vis[x][y] = 1;
cnt++;
x--;
}
x++, y++;
}
return res;
}
};
剑指 Offer 22. 链表中倒数第k个节点
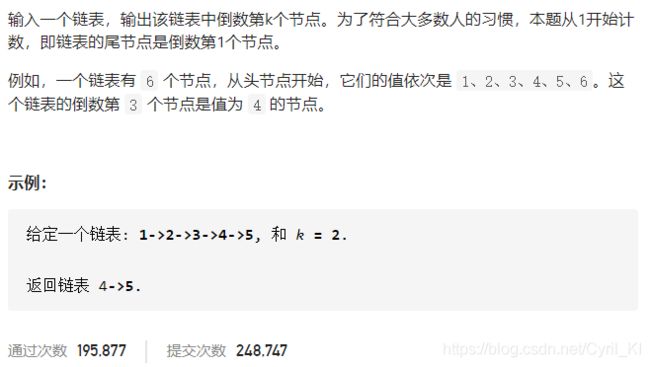
分析:
先得到链表的长度n,然后从头结点开始数n-k结点即为倒数第k个结点。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* getKthFromEnd(ListNode* head, int k) {
if(!head) {
return NULL;
}
int cnt = 1;
ListNode* ptr = head;
while(ptr->next) {
ptr = ptr->next;
cnt++;
}
for(int i = 0; i < cnt - k; i++) {
head = head->next;
}
return head;
}
};
剑指 Offer 17. 打印从1到最大的n位数
class Solution {
public:
vector<int> printNumbers(int n) {
vector<int> res;
long long end = (long long)pow(10, n);
for(long long i = 1; i < end; i++) {
res.push_back(i);
}
return res;
}
};
剑指 Offer 24. 反转链表

方法一:
先顺序保存链表中所有节点的值,然后逆序生成一个新的链表。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* reverseList(ListNode* head) {
if(!head) {
return nullptr;
}
ListNode* ptr = head;
vector<int> d;
while(ptr) {
d.push_back(ptr->val);
ptr = ptr->next;
}
int n = d.size();
ListNode* wail = new ListNode(d[n - 1]);
ListNode* p = wail;
for(int i = n - 2; i >= 0; i--) {
ListNode* temp = new ListNode(d[i]);
p->next = temp;
p = p->next;
}
p->next = nullptr;
return wail;
}
};
方法二:
在遍历链表时,将当前节点的next指针改为指向前一个节点。由于节点没有引用其前一个节点,因此必须事先存储其前一个节点。在更改引用之前,还需要存储后一个节点。最后返回新的头引用。
代码:
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* prev = nullptr;
ListNode* curr = head;
while (curr) {
ListNode* next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
return prev;
}
};
剑指 Offer 18. 删除链表的节点

分析:
遍历寻找到要删除的节点的前一个节点,然后进行删除操作。
代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* deleteNode(ListNode* head, int val) {
if(!head) {
return NULL;
}
ListNode* ptr = new ListNode(0);
ptr->next = head;
ListNode* res = ptr;
while(ptr) {
if(ptr->next->val == val) {
ptr->next = ptr->next->next;
return res->next;
}else {
ptr = ptr->next;
}
}
return res->next;
}
};
剑指 Offer 40. 最小的k个数
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
if(arr.empty()) {
return {
};
}
sort(arr.begin(), arr.end());
vector<int> res(arr.begin(), arr.begin() + k);
return res;
}
};
方法二:
用一个大根堆实时维护数组的前k小值。首先将前k个数插入大根堆中,随后从第k+1个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。c++中的大根堆为priority_queue
代码:
class Solution {
public:
vector<int> getLeastNumbers(vector<int>& arr, int k) {
vector<int> vec(k, 0);
if (k == 0) {
// 排除 0 的情况
return vec;
}
priority_queue<int> Q;
for (int i = 0; i < k; ++i) {
Q.push(arr[i]);
}
for (int i = k; i < (int)arr.size(); ++i) {
if (Q.top() > arr[i]) {
Q.pop();
Q.push(arr[i]);
}
}
for (int i = 0; i < k; ++i) {
vec[i] = Q.top();
Q.pop();
}
return vec;
}
};
剑指 Offer 30. 包含min函数的栈

分析:
使用一个辅助栈保存当前栈中的最小值。进栈时如果辅助栈为空或者其栈顶元素大于当前入栈元素,则更新辅助栈栈顶元素。出栈时如果出栈元素等于辅助栈栈顶元素,则辅助栈也要进行出栈操作。取最小值时,返回辅助栈的栈顶元素即可。
代码:
class MinStack {
public:
/** initialize your data structure here. */
stack<int> stk;
stack<int> stk_min;
MinStack() {
}
void push(int x) {
stk.push(x);
if(stk_min.empty() || x <= stk_min.top()) {
stk_min.push(x);
}
}
void pop() {
if(stk_min.top() == stk.top()) {
stk_min.pop();
}
stk.pop();
}
int top() {
return stk.top();
}
int min() {
return stk_min.top();
}
};
剑指 Offer 42. 连续子数组的最大和

分析:
令dp[i]表示以nums[i]结尾时所能取得的最大和。边界条件:dp[0] = nums[0]。如果dp[i - 1] < 0,则dp[i]就为nums[i],否则为dp[i - 1] + nums[i]。
代码:
class Solution {
public:
int maxSubArray(vector<int>& nums) {
vector<int> res;
int n = nums.size();
res.push_back(nums[0]);
for(int i = 1; i < n; i++) {
if(res[i - 1] > 0) {
res.push_back(res[i - 1] + nums[i]);
}else {
res.push_back(nums[i]);
}
}
sort(res.begin(), res.end(), greater<int>());
return res[0];
}
};
剑指 Offer 39. 数组中出现次数超过一半的数字

分析:
利用哈希表统计每个数出现的个数,然后返回满足条件的值。
代码:
class Solution {
public:
int majorityElement(vector<int>& nums) {
unordered_map<int, int> mp;
int n = nums.size();
for(int x : nums) {
mp[x]++;
if(mp[x] > n / 2) {
return x;
}
}
return 0;
}
};