优先级队列-堆【数据结构】

前言：
我们之前学习的普通的队列，元素是先进先出；而优先级队列，是按照顺序进，优先级最高的先出队列，优先级相同再遵循先进先出
优先级队列，名字叫队列，本质上是一个特殊的二叉树(堆)

举例：
幼儿园放学时，家长去接娃，整整齐齐的排着队等着进去接娃，突然来了一位校领导进学校有事…
.

二叉树的顺序存储

之前我们学习了二叉树的表示方法：左右孩子表示法，每个节点均记录左右子树的根节点引用
除此之外，我们也可以使用数组来表示一棵树

使用数组存储这棵树的层序变量结果(包含空节点)

但是，使用数组来表示树，可能会浪费很多的空间
比如：

对于一般的普通的树来说，使用数组表示，可能会造成空间的浪费，但是对于一种特殊的树(完全二叉树)来说，使用数组来表示就刚刚好，不会造成空间的浪费

完全二叉树： 和满二叉树相比，右侧缺了一个 “豁” (哈哈哈，比较容易理解~~)

堆(heap)

概念

在 JVM 内存区域划分(JVM内存模型 JMM)中，我们提到了方法区、栈区、堆区，程序计数器…
但是，今天提到的 堆 和 JVM 内存区域划分中的堆没关系 (此堆非彼堆)

堆(heap)，是数据结构中的通用概念，本质上是一个二叉树
.

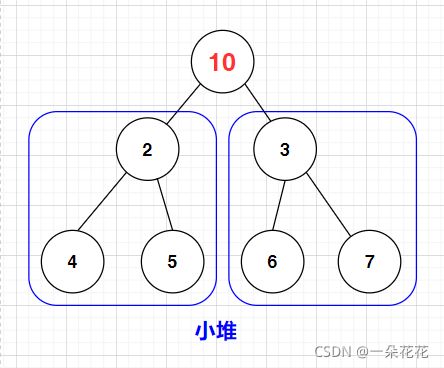
• 是一个完全二叉树
• 对于任意节点，满足根节点小于左右子树的值(小堆) 或 满足根节点大于左右子树的值(大堆)
• 堆通常是通过数组的形式来存储的
• 堆的最大用处：能够让我们快速找到树中的最大值或者最小值 (堆顶元素)
  还能帮我们高效的找出前 K 大 / 小 元素 topK问题

topK 问题

操作

向下调整

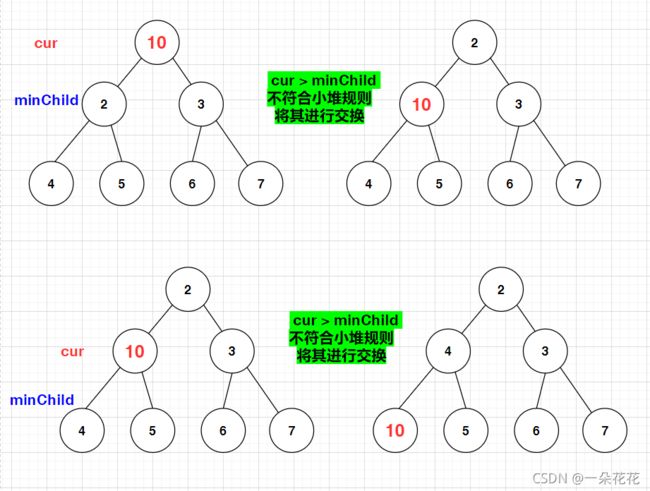
把不满足堆的结构调整成满足堆的结构

前提： 左右子树必须已经是一个堆，才能调整

过程：

• 设定根节点为当前节点 cur
• 比较其左右子树的值，使用 minChild 来标记较小的值
• 比较 minChild 和 cur 的值
  若 cur < minChild，即符合小堆规则，不进行交换，调整结束
  若 cur > minChild，不符合小堆规则，将其进行交换

代码实现：

时间复杂度： O(logN) — cur 固定，minChild 每次 x 2

private
 static void shiftDown(int[] array,int size,int index){
     
    // size 表示有效堆的 堆元素个数
    // index 表示从哪个位置的下标开始调整
    // cur 从 index 这里出发
    int cur = index;
    // 根据cur下标找到左子树的下标
    int minChild = cur * 2 + 1;
    while(minChild < size){
     
        //比较左右子树，找到较小值
        if(minChild + 1 < size && array[minChild + 1] < array[minChild]){
     
            minChild = minChild + 1;
        }
        // 此时minChild下标对应左右子树的较小值的下标
        // 比较 minChild 和 cur 的值
        if(array[cur] > array[minChild]){
     
            int tmp = array[minChild];
            array[minChild] = array[cur];
            array[cur] = tmp;
        }
        //调整结束
        else {
     
            break;
        }
        //更新 cur 和minChild
        cur = minChild;
        minChild = cur * 2 + 1;
    }
}

建堆

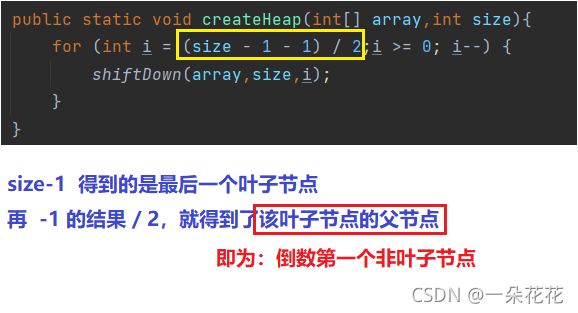
借助向下调整，就可以把一个数组构造成堆，从倒数第一个非叶子节点开始，从后往前遍历数组，针对每个位置，依次向下调整即可

举例： 将数组 [ 9，5，2，7，3，6，8 ] 建成一个小堆
过程分析：

代码实现：

public static void createHeap(int[] array,int size){
     
    for (int i = (size - 1 - 1) / 2;i >= 0; i--) {
     
        shiftDown(array,size,i);
    }
}

时间复杂度： 循环调用向下调整方法，时间复杂度看起来像是 O(logN*N)，但实际上是O(N) (复杂的数学推导过程)

向上调整 (以大堆为例)

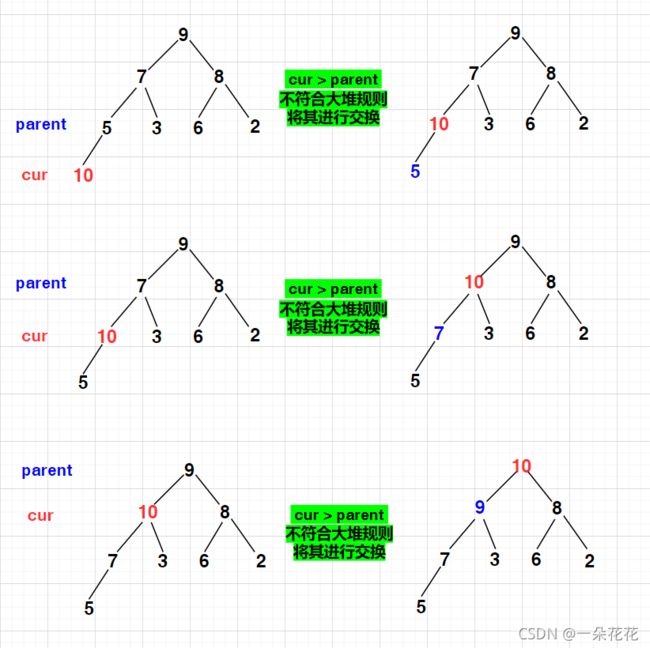
过程：

• 设当前节点 cur
• 比较 cur 和其父节点 parent 的值
  若 cur < parent，不符合大堆规则，将其进行交换
  若 cur > parent，即符合大堆规则，不进行交换，调整结束

由上可看出，向上调整比向下调整要简单些，直接比较父子节点即可

代码实现：

此处发现，没有用到 size参数，判定调整结束，只需要和 0 比较即可，不需要知道整个堆有多大

//向上调整
private static void shiftUp(int[] array,int size,int index){
     
    int cur = index;
    int parent = (cur - 1) / 2;
    while(cur > 0){
     
        //父亲比孩子大，不符合大堆要求
        if(array[parent] < array[cur]){
     
            //交换
            int tmp = array[parent];
            array[parent] = array[cur];
            array[cur] = tmp;
        }
        else{
     
            break;
        }
        cur = parent;
        parent = (cur - 1) / 2;
    }
}

使用堆模拟实现优先级队列

• 入队列

public void offer(int x){
     
    array[size] = x;
    size++;
    //把新加入的元素向上调整
    shiftUp(array,size-1);
}

• 出队列

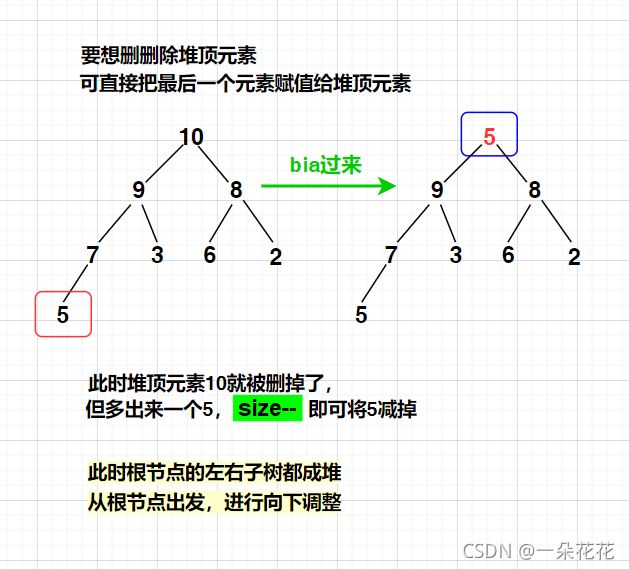
队首元素删掉的同时，满足剩下的结构仍然是一个堆

//出队列
public int poll(){
     
    //下标为0的元素即为堆顶元素
    int deleteVal = array[0];
    // 将最后一个元素 bia 到 堆顶元素
    array[0] = array[size - 1];
    size--;
    shiftDown(array,size,0);
    return deleteVal;
}

• 取堆顶元素

public int peek(){
     
    return array[0];
}

main方法验证：

public static void main(String[] args) {
     
    MyPriorityQueue queue = new MyPriorityQueue();
    queue.offer(9);
    queue.offer(5);
    queue.offer(2);
    queue.offer(7);
    queue.offer(3);
    queue.offer(6);
    queue.offer(8);

    //依次出队列
    while(!queue.isEmpty()){
     
        int cur = queue.poll();
        System.out.print(cur + " ");
    }
}

堆(优先队列)，每次poll一个元素都是把优先级最高 / 低的元素取出来，能帮我们解决 topK 问题，如果你 poll 了 n 次的话，就相当于对原来的序列进行了排序 — 堆排序

标准库中的优先队列

• 使用时必须导入PriorityQueue所在的包：

import java.util.PriorityQueue;

PriorityQueue是线程不安全的，而PriorityBlockingQueue是线程安全的

代码示例：

import java.util.PriorityQueue;

public class TestPriorityQueue {
     
    public static void main(String[] args) {
     
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        queue.offer(9);
        queue.offer(5);
        queue.offer(2);
        queue.offer(7);
        queue.offer(3);
        queue.offer(6);
        queue.offer(8);
        while(!queue.isEmpty()){
     
            int cur = queue.poll();
            System.out.print(cur + " ");
        }
    }
}

输出结果：

我们会发现，在标准库中，优先队列，默认是以小堆实现的

• 不能插入null对象，否则会抛出NullPointerException异常

• 不能插入无法比较大小的对象，否则会抛出ClassCastException异常

topK 问题

经典 topK 问题：
给定你 100 亿个数字，找出其中前1000大的元素(不考虑内存空间)

方法1:
用一个数组保存这100亿个数字，直接在这个数组上建大堆，循环1000次取出堆顶元素 + 调整操作，即可得到前1000大元素

方法2:

先取集合中的前1000个元素放到一个数组中，建一个小堆
一个一个遍历集合中的数字，将其和堆顶元素进行比较，若某个元素比堆顶元素大，就把堆顶元素删除(调整堆)，当所有元素遍历完后，堆中元素就是前1000大元素

时间复杂度分析：
假设给定 N 个元素，取前 M 大个元素 ( N 远大于M )

由上边的分析可见，方法2的效率更高

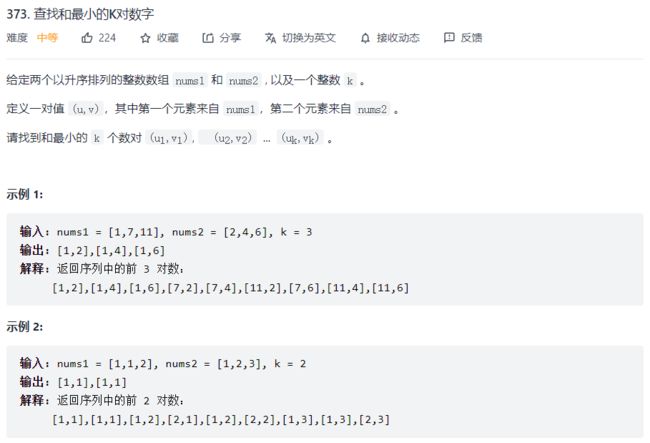
查找和最小的K对数字

在线OJ

思考：

• 获取到所有的数对
• 把数对放到优先队列中
  把数对放在一个类中，优先队列保存这个类即可
• 从优先队列中取前K对数对即可
  返回值的二维数组中，每一行是一个数对(两个元素)，一共有K行

代码实现：

以方法1 为例：

class Pair implements Comparable<Pair> {
     
    public int n1;
    public int n2;
    public int sum;

    public Pair(int n1, int n2) {
     
        this.n1 = n1;
        this.n2 = n2;
        this.sum = n1 + n2;
    }

    @Override
    public int compareTo(Pair o) {
     
        //this 比 other 小，返回 < 0
        //this 比 other 大，返回 > 0
        //this == other ，返回  0
        return this.sum - o.sum;
    }
}

public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
     
    List<List<Integer>> result = new ArrayList<>();
    //判断 nums1 nums2合法性
    if(nums1.length == 0 || nums2.length == 0 || k <= 0){
     
        return result;
    }
    //建立一个小堆
    PriorityQueue<Pair> queue = new PriorityQueue<>();
    //获取到所有可能的数对,并加入到队列中
    for (int i = 0; i < nums1.length; i++) {
     
        for (int j = 0; j < nums2.length; j++) {
     
            queue.offer(new Pair(nums1[i],nums2[j]));
        }
    }
    //循环取出前k项元素
    for (int i = 0; i < k && !queue.isEmpty(); i++) {
     
        Pair cur = queue.poll();
        List<Integer> tmp = new ArrayList<>();
        tmp.add(cur.n1);
        tmp.add(cur.n2);
        result.add(tmp);
    }
    return result;
}