《数据结构、算法与应用 —— C++语言描述》学习笔记 — 平衡搜索树 — AVL 树
《数据结构、算法与应用 —— C++语言描述》学习笔记 — 平衡搜索树 — AVL 树
- 一、AVL 树
-
- 1、定义
- 2、高度
- 3、描述
- 4、搜索
- 5、插入
-
- （1）特点
- （2）旋转
- （3）算法
- 6、删除
- 二、实现
-
- 1、节点类修改
- 2、二叉树修改
- 3、BST 修改
-
- （1）hotParent
- （2）查找接口
- （3）插入接口
- （4）删除接口
- （5）更新父节点接口
- 4、AVL声明
- 5、3+4重构
- 6、旋转
- 7、平衡
- 8、插入
- 9、删除
- 10、测试代码
一、AVL 树
如果搜索树的高度总是 O ( l o g n ) O(logn) O(logn)，我们就能保证查找、插入和删除的时间为 O ( l o g n ) O(logn) O(logn)。最坏情况下的高度为 O ( l o g n ) O(logn) O(logn)的树称为平衡树。比较流行的一种平衡树是 AVL 树。
1、定义
一棵空的二叉树是 AVL 树；如果 T 是一个非空的二叉树， T L T_L TL和 T R T_R TR分别是其左子树和右子树，那么当 T 满足以下条件时，T 是一棵 AVL 树：
① T L T_L TL和 T R T_R TR是 AVL 树
② ∣ h L − h R ∣ ≤ 1 |h_L-h_R|\le1 ∣hL−hR∣≤1，其中 h L h_L hL和 h R h_R hR分别 T L T_L TL和 T R T_R TR的高
一棵 AVL 搜索树既是二叉搜索树，也是 AVL 树。一棵索引 AVL 搜索树既是索引二叉搜索树，也是 AVL 树。
如果用 AVL 树来描述字典，并在对数级时间内完成每一种字典操作，那么，我们必须确定 AVL 树的以下特征：
① 一棵 n 个元素的 AVL 树，其高度是 O ( l o g n ) O(logn) O(logn)。
② 对于每一个 n，都存在一棵 AVL 树。
③ 对一棵 n 元素的 AVL 搜索树，在 O ( l o g n ) O(logn) O(logn)的时间内可以实现查找。
④ 将一个新元素插入一棵 n 元素的 AVL 搜索树中，可以得到一棵 n+1 个元素的 AVL 树，而且插入用时 O ( l o g n ) O(logn) O(logn)。
⑤ 一个元素从一棵 n 元素的 AVL 搜索树中删除，可以得到一棵 n-1 个元素的 AVL 树，而且删除用时为 O ( l o g n ) O(logn) O(logn)。
2、高度
对一棵高度为 h 的 AVL 树，令 N h N_h Nh是其最少的节点数。在最坏情况下，根的一棵子树的高度是 h-1，另一棵子树的高度是 h - 2，而且两棵子树都是 AVL 树。因此有： N h = N h − 1 + N h − 2 + 1 ， N 0 = 0 且 N 1 = 1 N_h=N_{h-1}+N_{h-2}+1，N_0=0且N_1=1 Nh=Nh−1+Nh−2+1，N0=0且N1=1不难发现，此定义和斐波那契数列的定义是相似的。因此，如果书中有 n 个节点，那么树的最大高度为： log φ ( 5 ( n + 1 ) ) − 2 ≈ 1.44 log 2 ( n + 2 ) = O ( l o g n ) \log_φ{(\sqrt5(n+1))}-2\approx1.44\log_2{(n+2)}=O(logn) logφ(5(n+1))−2≈1.44log2(n+2)=O(logn)
3、描述
AVL 树一般用链表描述。但是，为简化插入和删除操作，我们为每个节点增加一个平衡因子 bf。节点 x 的平衡因子 b f ( x ) bf(x) bf(x)定义为：x 的左子树高度 - x 的右子树高度。
从 AVL树的定义可知，平衡因子的取值范围可能为-1、0、1
4、搜索
AVL 搜索树的搜索功能可以直接使用二叉搜索树的相应函数实现。
5、插入
如果我们直接使用二叉搜索树的插入函数，可能导致 AVL 树不再是一棵平衡树。如图：
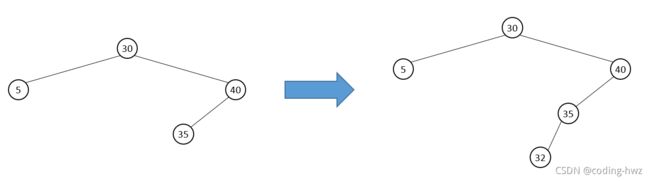图中根节点所对应的子树的平衡因子不再满足平衡条件。如果一棵 AVL 树中，有一个或多个节点不满足平衡条件，那么这棵 AVL 树就是不平衡的。我们可以通过移动不平衡树的子树恢复平衡：
（1）特点
为了恢复平衡，我们可以观察插入节点后导致失衡这一过程中的共同点：
① 在不平衡树中，平衡因子的值限于-2，-1，0，1，2
② 平衡因子为2的节点在插入前的平衡因子为1。类似地，平衡因子为-2的节点在插入前的平衡因子为-1。
③ 只有从根到新插入节点的路径上的节点，其平衡因子在插入后会改变。
④ 假设A是离新插入节点最近且平衡因子是-2或2的祖先，在插入前，从A到新插入节点的路径上，所有节点的平衡因子都是0。
针对④我们简单证明一下。假如存在从A到新插入节点路径上的某个节点X的平衡因子不是0（其余节点均为0），以1为例：说明此节点左右子树高度差为 h L − h R = 1 h_L-h_R=1 hL−hR=1。下面我们插入一个节点。若此节点插入到X的右子树中，显然，X所对应的子树高度不会发生变化，那么树的平衡性也不会被改变；若此节点插入到X的左子树中，由于其左子树为满二叉树，因此，该节点将改变左子树的高度。进而我们会发现该节点左右子树高度差变为 h L − h R = 2 h_L-h_R=2 hL−hR=2。那么此时，A不再是离新插入节点最近的平衡因子为2的祖先，假设被推翻。因此④成立。
（2）旋转
节点A的不平衡情况有两类：L型不平衡（新插入节点在A的左子树）和R型不平衡（新插入节点在A的右子树）。在从根到新插入节点的路径上，根据A的孙节点情况A的不平衡情况还可以细分。注意，包含新节点的A的子树高度至少是2，A才存在这样的孙节点。A的不平衡类型的细分为：LL（新插入节点在A节点的左子树的左子树中），LR（新插入节点在A节点的左子树的右子树中），RR和RL。
我们以LL型和LR型不平衡为例说明如何实施旋转操作：
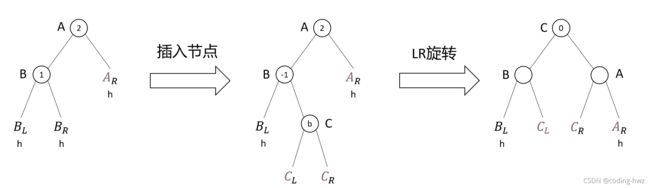
RR和RL与上面的图示是对称的。我们把矫正LL和RR型不平衡所做的转换称为单旋转，把矫正LR和RL型不平衡所做的转换称为双旋转。对LR型不平衡所做的转换可以看做RR旋转加LL旋转，而对RL型不平衡所做的双旋转可以看做LL旋转加RR旋转。
不难看出，经过旋转后子树的高度不会发生变化。
（3）算法
① 沿着从根节点开始的路径，根据新元素的关键字，去寻找新元素的插入位置。在此过程中，记录最新发现平衡因子为-1或1的节点，并令其为A节点。如果找到了具有相同关键字的元素，那么插入失败，终止算法。
② 如果没有找到这样的A节点，那么从根节点开始沿着插入路径修改平衡因子，然后终止算法。
③ 如果 bf(A) = 1 并且新节点插入A的右子树中，或者 bf(A) = -1 并且新节点插入到左子树，那么修改从A到新节点路径中节点的平衡因子，然后终止算法。
④ 确定 A 的不平衡类型并执行相应的旋转，并对新子树根节点至新插入节点的路径上的节点的平衡因子做相应的修改。
此算法的时间复杂度为 O ( l o g n ) O(logn) O(logn)。
6、删除
类似地，删除操作也可能导致不平衡情况的出现。令A是从删除节点到根节点路径上第一个不平衡的节点。要恢复A节点的平衡，需要根据不平衡的类型而定。如果删除发生在A的左子树，那么不平衡类型是L型；否则，不平衡类型就是R型。如果在删除后，bf(A)=2，那么在删除前，bf(A) 的值一定为1。因此，A有一棵以B为根的左子树。根据 bf(B) 的值，可以把一个R型不平衡细分为R0，R1和R-1。例如，R-1型不平衡指的是这种情况：删除操作发生在A的右子树并且 bf(B)=-1。下面我们以R型为例，图示不同类型不平衡节点的旋转：
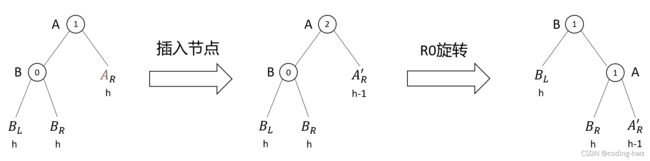
R1型旋转与R0型旋转类似，区别在于，R1型旋转操作后，子树的高度发生了变化，从h+2变为h+1。这种变化可能导致其他子树失衡。因此，R1型旋转的是时间复杂度为 O ( l o g n ) O(logn) O(logn)。
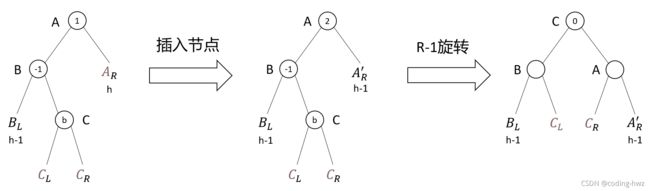
LL与R1类型的旋转相同，LL与R0型旋转的区别仅在于A和B最后的平衡因子；LR与R-1旋转相同。
此算法的时间复杂度为 O ( l o g n ) O(logn) O(logn)。
二、实现
这里我们需要节点和树的一些额外信息，因此需要先修改前面的部分代码实现
1、节点类修改
在AVL树中，我们需要计算每个节点的高度。如果我们每次都使用原来递归的方式计算，无疑会有大量重复。因此，我们将高度信息保存在节点中，由树负责更新高度。除此之外，我们增加了获取更高的孩子的接口，用于旋转使用。
template<typename T>
class binaryTreeNode
{
public:
int height;
binaryTreeNode(const T& element, binaryTreeNode* leftChild = nullptr, binaryTreeNode* rightChild = nullptr, binaryTreeNode* parent = nullptr) :
element(element)
{
...
this->height = 0;
}
}
template<typename T>
inline binaryTreeNode<T>* binaryTreeNode<T>::tallerChild()
{
if (rightChild == nullptr)
{
return leftChild;
}
else if (leftChild == nullptr)
{
return rightChild;
}
else
{
return leftChild->height >= rightChild->height ? leftChild : rightChild;
}
}
2、二叉树修改
二叉树增加了更新高度接口，修改了高度的计算方式。
#define stature(p) ((p) ? (p)->height : -1)
template<typename T>
inline int linkedBinaryTree<T>::height()
{
return root == nullptr ? -1 : root->height;
}
template<typename T>
inline void linkedBinaryTree<T>::updateHeight(binaryTreeNode<T>* node)
{
node->height = std::max(stature(node->leftChild), stature(node->rightChild)) + 1;
}
3、BST 修改
前面我们实现的BST有点小问题，考虑了重复元素的插入，但是在代码中没有完全体现。这次我们换一种实现方式，使其看起来更合理，同时减少代码冗余。
（1）hotParent
mutable NodeType* hotParent = nullptr;
我们在类声明中增加一个变量用以表示查找过程中的父节点。
（2）查找接口
template<typename Key, typename Value>
inline auto BinarySearchTree<Key, Value>::findNode(const Key& key) const ->BinarySearchTree<Key, Value>::NodeType*
{
auto currentNode = this->root;
hotParent = nullptr;
while (currentNode != NULL)
{
if (key == currentNode->element.first)
{
return currentNode;
}
else
{
hotParent = currentNode;
if (key < currentNode->element.first)
{
currentNode = currentNode->leftChild;
}
else
{
currentNode = currentNode->rightChild;
}
}
}
return nullptr;
}
（3）插入接口
template <typename Key, typename Value>
inline void BinarySearchTree<Key, Value>::insert(const ValueType& element)
{
auto node = findNode(element.first);
if (node != nullptr)
{
node->element.second = element.second;
return;
}
insertElementWithParent(element, hotParent);
this->treeSize++;
}
这里我们实际是将查找过程中得到的父节点作为冗余信息保存在对象中。
（4）删除接口
我们将删除接口中的部分操作封装到函数 removeAt 中：
template <typename Key, typename Value>
inline void BinarySearchTree<Key, Value>::erase(const Key& key)
{
auto deleteNode = findNode(key);
if (deleteNode == nullptr)
{
return;
}
removeAt(deleteNode);
}
template<typename Key, typename Value>
inline void BinarySearchTree<Key, Value>::removeAt(NodeType* node)
{
swapNodeWithSuccessor(node);
removeNodeWithNoOrSingleChild(node);
delete node;
this->treeSize--;
}
（5）更新父节点接口
我们新增更新父节点接口，用于将一个节点的父亲更新为另一个节点。由于此处替换可能导致根元素的修改，因此没有放在节点类中实现。
template<typename Key, typename Value>
inline void BinarySearchTree<Key, Value>::updateParent(NodeType* parent, NodeType* originalChild, NodeType* newChild)
{
newChild->parent = parent;
if (parent != nullptr)
{
parent->leftChild == originalChild ? parent->leftChild = newChild : parent->rightChild = newChild;
}
else
{
this->root = newChild;
}
}
4、AVL声明
#pragma once
#include "../binarySearchTree/BinarySearchTree.h"
template<typename Key, typename Value>
class AVL : public BinarySearchTree<Key, Value>
{
public:
using typename BinarySearchTree<Key, Value>::ValueType;
using typename BinarySearchTree<Key, Value>::NodeType;
virtual void erase(const Key& key) override;
virtual void insert(const ValueType& element) override;
protected:
int balancedFactor(NodeType* node);
bool isBalanced(NodeType* node);
NodeType* connect34(NodeType* node0, NodeType* node1, NodeType* node2, NodeType* t0, NodeType* t1, NodeType* t2, NodeType* t3);
NodeType* rotateAt(NodeType* node);
};
5、3+4重构
不难发现，这里我们最重要的函数就是旋转函数的实现。仔细观察各种情况，不难发现所有旋转的实现都是3+4重构。什么是3+4重构呢？假设，在插入或删除节点后，离新节点或被删除节点最近的失衡节点为g。若g，g较高的孩子p，p较高的孩子n三个节点的中序遍历顺序为n0，n1，n2，它们的子树（不包括这几个节点）从左到右依次为T0，T1，T2，T3。那么旋转后的结果为：
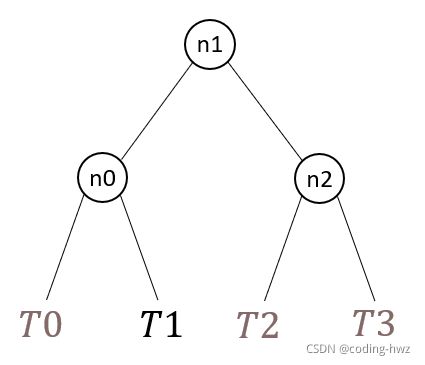
以LR旋转为例：
其实现代码如下：
template<typename Key, typename Value>
inline auto AVL<Key, Value>::connect34(NodeType* node0, NodeType* node1, NodeType* node2,
NodeType* t0, NodeType* t1, NodeType* t2, NodeType* t3) -> NodeType*
{
node0->leftChild = t0;
node0->rightChild = t1;
if (t0 != nullptr)
{
t0->parent = node0;
}
if (t1 != nullptr)
{
t1->parent = node0;
}
this->updateHeight(node0);
node2->leftChild = t2;
node2->rightChild = t3;
if (t2 != nullptr)
{
t2->parent = node2;
}
if (t3 != nullptr)
{
t3->parent = node2;
}
this->updateHeight(node2);
node1->leftChild = node0;
node1->rightChild = node2;
node0->parent = node1;
node2->parent = node1;
this->updateHeight(node1);
return node1;
}
6、旋转
旋转的主要作用在于确定3+4重构的节点和树的对应关系：
template<typename Key, typename Value>
inline auto AVL<Key, Value>::rotateAt(NodeType* node) -> NodeType*
{
auto parentNode = node->parent;
auto grandparentNode = parentNode->parent;
if (grandparentNode->leftChild == parentNode)
{
if (parentNode->leftChild == node)
{
this->updateParent(grandparentNode->parent, grandparentNode, parentNode);
return connect34(node, parentNode, grandparentNode,
node->leftChild, node->rightChild, parentNode->rightChild, grandparentNode->rightChild);
}
else
{
this->updateParent(grandparentNode->parent, grandparentNode, node);
return connect34(parentNode, node, grandparentNode,
parentNode->leftChild, node->leftChild, node->rightChild, grandparentNode->rightChild);
}
}
else
{
if (parentNode->leftChild == node)
{
this->updateParent(grandparentNode->parent, grandparentNode, node);
return connect34(grandparentNode, node, parentNode,
grandparentNode->leftChild, node->leftChild, node->rightChild, parentNode->rightChild);
}
else
{
this->updateParent(grandparentNode->parent, grandparentNode, parentNode);
return connect34(grandparentNode, parentNode, node,
grandparentNode->leftChild, parentNode->leftChild, node->leftChild, node->rightChild);
}
}
}
7、平衡
平衡因子只需计算子树的高度差的绝对值：
template<typename Key, typename Value>
inline int AVL<Key, Value>::balancedFactor(NodeType* node)
{
return (node->leftChild != nullptr ? node->leftChild->height : -1) -
(node->rightChild != nullptr ? node->rightChild->height : -1);
}
template<typename Key, typename Value>
inline bool AVL<Key, Value>::isBalanced(NodeType* node)
{
return std::abs(balancedFactor(node)) < 2;
}
8、插入
与我们前面的说明类似，插入接口在找到一个失衡节点并旋转后，不需再处理其祖先节点：
template<typename Key, typename Value>
inline void AVL<Key, Value>::insert(const ValueType& element)
{
auto node = this->findNode(element.first);
if (node != nullptr)
{
node->element.second = element.second;
return;
}
this->insertElementWithParent(element, this->hotParent);
this->treeSize++;
node = new NodeType(element, nullptr, nullptr, this->hotParent);
for (auto parentNode = node->parent; parentNode != nullptr; parentNode = parentNode->parent)
{
if (!isBalanced(parentNode))
{
rotateAt(parentNode->tallerChild()->tallerChild());
break;
}
else
{
this->updateHeight(parentNode);
}
}
}
9、删除
删除节点后，我们仍需处理其祖先节点，因此循环中没有 break。此外，节点旋转后，正在遍历的子树的根节点实际已经发生变化，需要更新。这也是我们前面3+4重构将新根节点返回的原因。
template<typename Key, typename Value>
inline void AVL<Key, Value>::erase(const Key& key)
{
auto node = this->findNode(key);
if (node == nullptr)
{
return;
}
this->removeAt(node);
for (node = this->hotParent; node != nullptr; node = node->parent)
{
if (!isBalanced(node))
{
node = rotateAt(node->tallerChild()->tallerChild());
}
this->updateHeight(node);
}
}
10、测试代码
书中没有提供测试代码，我自己写了一个测试代码，将这些情况都测试了一次：
#pragma once
#include 测试结果如下：
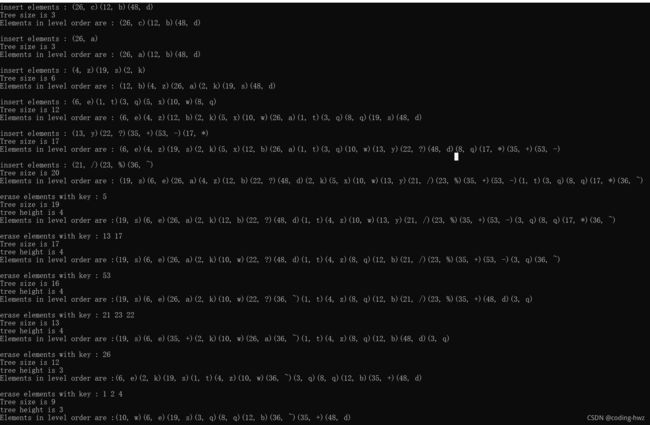
最后，书中并没有提到3+4重构。该原理及相关实现可以参考清华大学邓俊辉数据结构与算法【完】。AVL树的实现我也参考了其中的材料。