python - 啃书 第七章 模块、包和库 (二)
常用第三方库
Pandas
Pandas 中文网
Pandas是基于NumPy库的一种解决数据分析任务的工具库
Pandas库纳入了大量模块和一些标准的数据模型,提供了高效的操作大型数据集所需的工具
Pandas库的主要功能有:
创建Series(系列)和DataFrame(数据帧)、索引选取和过滤、算术运算、数据汇总和描述性统计、数据排序和排名、处理缺失值和层次化索引等
系列 Series
系列与NumPy库中的一维数组(array)类似,能保存字符串、Bool值、数字等不同的数据类型
创建格式:pands.Series(data,index,dtype,copy)
data:数据,采取各种形式,如ndarray、list、constants等
index:索引值,必须是唯一的和散裂的
dtype:数据类型
copy:复制数据,默认为False
import pandas as pd
import numpy as np
data=np.array(['需求分析','概要设计','详细设计','编制代码','运行维护'])
s=pd.Series(data)
print(s)
#
0 需求分析
1 概要设计
2 详细设计
3 编制代码
4 运行维护
dtype: object
从字典创建一个系列
import pandas as pd
d={
'A':"优秀",'B':"良好",'C':"合格",'D':"不合格"}
s=pd.Series(d)
print(s)
print("s[0]:",s[0])
print("s['A']:",s['A'])
print("s[0]'s key:",s.index[0])
#
A 优秀
B 良好
C 合格
D 不合格
dtype: object
s[0]: 优秀
s['A']: 优秀
s[0]'s key: A
与字典的不同之处,索引方面,pd既可以用index索引,又可以用key索引。而字典只能用key索引。
但是效率方面还是字典更高一筹
"D" in d # 49.7 ns
"D" in s # 799 ns
"不合格" in d.values() # 237 ns
"不合格" in s.values # 6.54 µs
那么Series的意义:
pandas 学习(1): pandas 数据结构之Series
里面介绍到pandas同时拥有字典和数组的结构,算是融合了两者的使用,又增加了字典没有的index索引,和对齐输出。
那么就只看看对齐输出这项!
%%timeit
d={
'A':"优秀",'B':"良好",'C':"合格",'D':"不合格"}
s=pd.Series(d)
print(s)
883 µs / noprint 214 µs
那么字典实现对齐输出呢
字典一般是这种模式:可以考虑字符替换,但无法保证对齐,也可以考虑,循环输出
{‘A’: ‘优秀’, ‘B’: ‘良好’, ‘C’: ‘合格’, ‘D’: ‘不合格’}
A 优秀
B 良好
C 合格
DDDDDDDDDDDDDDDDDDDD 不合格
dtype: object
%%timeit
l=0
for i in d:
if len(i)>l:l=len(i)
for i in d:
print(i+" "*(l-len(i)),1)
补空格法,886 µs
%%timeit
l=0
for i in d:
if len(i)>l:l=len(i)
for i in d:
exec("print('%%-%ds 1'%%i)"%l)
exec + %-10s法,514 µs,因为不知道如何实现变量,突然想,如果exec在for外面的话
518 µs ,好奇并没有变化,推测exec和自定义函数变量一样,只生效第一次,不在变化,看似他在for里面,可能只执行了一次,而不是每次都执行!?
但是如果key中有中文的话,这个方法就不行了,但其实pd也并不能完美显示的样子
A 优秀
B 良好
1111 合格
ddddD瓦房 不合格
这里不再讨论对齐这个事情,接着啃书,计算unicode的个数快呢,还是使用decode快呢!?
数据帧(DataFrame)
数据帧是二维的表格型数据结构,即数据以行和列的表格方式排列。与系列相比,数据帧使用得更普遍。
pandas.DataFrame(data,index,columns,dtype,copy)
data: 数据,可以是各种类型,如ndarray、series、lists、dict、constant、DataFrame等
index,columns: 分别为行标签和列标签
dtype: 每列的数据类型
copy: 复制数据,默认值为False
从列表创建DataFrame
import pandas as pd
data=[['Tom',3],['Jerry',1]]
df=pd.DataFrame(data,columns=['Name','Age'])
print(df)
#
Name Age
0 Tom 3
1 Jerry 1
访问:
(1)df[r,c]: row: 行 column: 列 ???运行失败
(2)df.loc(r,c): 基于标签访问数据,函数中的r和c分别为行标签和列标签
(3)df.iloc(r,c): 基于整数访问数据,函数中的r和c分别为行标签索引和列标签索引
import numpy as np
import pandas as pd
df=pd.DataFrame(np.arange(9).reshape((3,3)),index=['A','B','C'],columns=['one','two','three'])
df
#
one two three
A 0 1 2
B 3 4 5
C 6 7 8
df[1:2]
# columns是一直显示的,index只决定哪一行会显示
one two three
B 3 4 5
df[['three','one']]
#
three one
A 2 0
B 5 3
C 8 6
df[['three','one']][1:2]
# 如果再分的细一点呢,但我觉得应该有更好的方法,530 µs df[1:2][['three','one']],556 µs
three one
B 5 3
df[df['three']>5]
one two three
C 6 7 8
df.loc['A','two']
#
1
df.loc['A']
one 0
two 1
three 2
Name: A, dtype: int32
df.loc['A':'B','one':'two']
one two
A 0 1
B 3 4
df.loc[['A','B'],['one','three']]
one three
A 0 2
B 3 5
df.loc['B',['three','one']]
three 5
one 3
Name: B, dtype: int32
468 µs
df.iloc[1,1]
#
4
df.iloc[1]
#
one 3
two 4
three 5
Name: B, dtype: int32
df.iloc[1:2]
one two three
B 3 4 5
df.iloc[[1,2]]
one two three
B 3 4 5
C 6 7 8
df.iloc[1,2]
5
pandas的DataFrame的行列选择
pandas 获取不符合条件/不包含某个字符串的dataframe
SciPy库
SciPy库是一款方便、易于使用、专为科学和工程设计的工具库,包括统计、优化、整合、线性代数、傅里叶变换、信号和图像处理、常微分方程求解等
scipy库中的模块很多,不同模块的功能相对独立,如scipy.constants(数学常量),scipy.fftpack(快速傅里叶变换)、scipy.integrate(积分)、scipy.optimize(优化算法)、scipy.stats(统计函数)、scipy.special(特殊数学函数)、scipy.signal(信号处理)、scipy.ndimage(N维图像、图像处理)模块等
维度:dimension
constants模块
from scipy import constants as con
con.hour
3600.0
con.c
299792458.0
con.inch
0.0254
con.degree
0.017453292519943295
con.golden
1.618033988749895
除了这些常数之外,还提供了诸多转换、计算方法。
special模块
from scipy import special as sp
sp.cbrt(27)
1.28 µs
pow(27,1/3) #精度不足
223 ns
sp.sindg(30) # 角度正弦
0.49999999999999994 # 又精度不足?
sp.comb(6,3) # 6选3的组合数
20.0
sp.perm(6,3) # 6选3的排列数
60.0
sp.round(5.5) # 四舍五入的整数
6.0
def square_root_1():
c = 27
g = c/2
i = 0
while abs(g**3 - c) > 0.00000000001:
g = (2*g)/3 + c/(3*(g**2)) #此为开三次方根的公式
i = i + 1
# print("% d: % .13f" % (i,g))
square_root_1()
5.45 µs
def 开方(n,x):
m=pow(n,1/x)
if m**x<n:
i=0.0000000000000001
while 1:
t=m+i
if t==m:i+=0.0000000000000001
else:
m=t
if m**x>=n:break
return m
n=64
x=3
开方(n,x)
1.18 µs
由于精度的问题,这里直接加0.0000000000000001可能数值不变,要么转成bin再+1进行处理!
struct pack float
精度问题通常都是b’@\x0b\xff\xff\xff\xff\xff\xff’模式,但是二进制的+1运算貌似就是很难,而且并不知道何时是真的需要+1。那运算上是否可以尝试,嗯… 其实除了网友提到的那个运算,还真没有举出反例的,用随机浮点随机一些反例吧!
平方与开平方都是没问题的,三次方不准确率高达95.8%
总之,开方的是2的次幂是准确的,虽然在256次方会提示数值过大,无法运算之类的,但是在运算之内都是准确的。几个质数偶尔准确率也相当的高。剩下的如上,三次方的准确率。
但是这个结果此时并非如上的\xff模式,甚至说随机出来的很难出现整数,纯粹是次幂结果就是不精确值吧!?
尝试下随机整数,或者顺序整数,看看其结果! 很确信的是1、2、3的三次方都没问题,但是4得3次方是不行了。而其他的未知精确结果的就不知道了。 那假设这里取得随机值是基数 {4: (3.9999999999999996, b’@\x0f\xff\xff\xff\xff\xff\xff’), 回归原题,即便是special的开方,也只能做到如此,例如: 先处理下这个吧!? 貌似又很简单,只需要转换成字符串再处理,就简单不过了! 假设一个使用e表示的数字! 0.00000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001 1e-323:b’\x00\x00\x00\x00\x00\x00\x00\x02’ 在这个数量级的运算误差,假设单位是1米,夸克的直径量级也不过是1e-18。而且基准单位真的后面这么串0的话,完全可以把基准单位往后设置! 但其实最小的是:5e-324:b’\x00\x00\x00\x00\x00\x00\x00\x01’ 回正题: 所以最直接的方法就是想办法在二进制上+1!且不说效率是否比纯数学求精度,循环+精度,至少这个很计算机!至于如何实现,很遗憾的是我目前并未找到直接的转二进制方法和二进制加减法的方法。需要自己去写。至于是否有意外情况,未知! 这个操作在numpy中也有,但是效率优秀 一维卷积运算 卷积神经网络与图像识别 我查了下什么是卷积,其实就是对较大数据压缩成较小数据,数据缩小后,处理量和特征都能得到提高,于是搜了下卷积与图像识别。这个也能用在音频识别上 理解图像卷积操作的意义 x: 于是我写了下这个,在jupyter中,显示耗时 作者是国人,目前就职于百度,同时还发现百度的飞桨开源计划 jieba.cut、jieba.cut_for_search:返回迭代器,可用for遍历 纳秒级,这就是大神 词频——你想文件频率TF-IDF算法进行关键词抽取 jieba支持创建自定义分词器 这里的迭代器并不能用list等转化,看来自定义模块可以接收常用函数并定义返回方式的。而for这种方式看来是最通用的! 这个仍然需要用pipe进行安装 cmd: 在Python中,用户可以编写具有特定功能的模块,保存到扩展名为.py的文件中。由用户自己编写的模块称为自定义模块。 pack A11调用A12 调用方法: ERROR:‘A12’ is not a package 在源文件main.py中调用包pack2中的模块A2 方法: ERROR:‘pack2.A2’ is not a package ERROR:module ‘pack2’ has no attribute ‘A2’ 从上面可以看出的规律: 错误: 导入无论是from A import B还是import A 这里sys.path.append支持.和…的用法 1、begin_fill和end_fill成对出现,填充期间代码所画 还有个问题就是眼镜镜片的折射问题 另外书中的例子看着好麻烦的样子,那最简化写法 如果把红色放在最后面再画,这涉及到的问题就是线条覆盖,turtle就是这样的东西,当然设计合适的话,可以再做一个混合颜色的功能,实现较好的过渡和视觉感。 至于用途,之后探索,但是可能不大适合放在web服务器端,这个运算量过大。 受用NumPy和Matplotlib对股票000001在2018年7月的交易数据进行分析并显示股票收盘价走势图 分析:股票000001在2018年7月的交易数据存储在文件000001_stock01.csv中,数据各列分别是date(日期)、open(开盘价)、high(最高价)、close(收盘价)、low(最低价)、volume(成交量)。 2018/7/2, 9.05, 9.05, 8.61, 8.55, 1315520.12 本案例中调用NumPy和Matplotlib中的相关函数实现了如下功能: 收盘价的算术平均价格: 8.63元 数据同上,不过为了Pandas添加了第一列 (1)使用imageio库中的imread()函数读取图像文件 Lossy conversion from float64 to uint8. Range [0.0, 255.0]. Convert image to uint8 prior to saving to suppress this warning.
3: (1.4422495703074083, b’?\xf7\x13tI\x12>\xf6’),
4: (1.5874010519681994, b’?\xf9e\xfe\xa5=n<’),
5: (1.7099759466766968, b’?\xfb\\x0f\xbc\xfe\xc4\xd3’),
7: (1.912931182772389, b’?\xfe\x9b]\xbaX\x18\x9d’),
10: (2.154434690031884, b’@\x01
6: (5.999999999999999, b’@\x17\xff\xff\xff\xff\xff\xff’),
7: (6.999999999999999, b’@\x1b\xff\xff\xff\xff\xff\xff’),
8: (7.999999999999999, b’@\x1f\xff\xff\xff\xff\xff\xff’),
9: (8.999999999999998, b’@!\xff\xff\xff\xff\xff\xff’),
10: (9.999999999999998, b’@#\xff\xff\xff\xff\xff\xff’),
这里不仅出现了ff结尾的,还有fe结尾的。而且小数点后有14、15、16位不等的结尾。如果按照这个规律去对比进位后结果,该怎么说呢还是开始递增结尾+1的思路最简单,例如86结尾的,尝试发现+4有效,顶多简单的循环四次,如果想的太复杂,可能性是一个局限。那么只要修正之前代码中,最末尾精度的问题了!貌似也并不是简单的事情!
sp.cbrt(63)
63**(1/3)
结果都是3.9790572078963917
他的下一个值是3.979057207896392
3次方结果分别是62.99999999999999
63.000000000000014
还是小的那个更加接近63。其实最关键的是我们并不知道python的基础平方算法。只能说他的结果并不准确,但他的运算速度着实迅速,作为单纯的编程者来说,我们只是要补正误差操作!但是最好的方法就是二进制+1,毕竟判断浮点的最小精度想想都是很困难的,我们要从小数点后多少位想到小数点前多少位。
120000000000000000000000000000000000.0**(1/3)
493242414866.0933
493242414866.094024658209**3
1.2000000000000003e+35
这个才是最接近结果的?
493242414866.094024658209
493242414866.09406
493242414866.09402465820
493242414866.094
493242414866.09402> :493242414866.094
493242414866.09403<=:493242414866.09406
所以计算机客观上的表示是493242414866.094最接近结果,也并非代码得出的493242414866.0933
1.199999999999995e+35 vs
1.1999999999999999e+35
至于意义,未曾可知!
毕竟几遍如浮点数,他要是结果真的如50vs99,存在吗?即便是import struct
struct.pack("!d",493242414866.09406)
b'B\\\xb5\xe2}\xc4\x86\x05'
struct.unpack("!d",b'B\\\xb5\xe2}\xc4\x86\x06')
(493242414866.0941,)
b'B\\\xb5\xe2}\xc4\x86\x04'
(493242414866.094,)
scipy.linalg 线性代数
import numpy as np
from scipy import linalg
mat=np.array([[5,6],[7,8]])
print("方阵:",mat)
print("方阵的行列式:%6.2f."%linalg.det(mat))
print("方阵的逆矩阵:",linalg.inv(mat))
#
方阵: [[5 6]
[7 8]]
方阵的行列式: -2.00.
方阵的逆矩阵: [[-4. 3. ]
[ 3.5 -2.5]]
linalg.det 7.2 µs
np.linalg.det 7.88
linalg.inv 9.19
np.linalg.inv 35.9signal 信号处理模块
import numpy as np
import scipy.signal
x=np.array([3,4,5])
h=np.array([6,7,8])
nn=scipy.signal.convolve(x,h)
print("nn:",nn)
#
nn: [18 45 82 67 40]
Matplotlib 2D绘图库
(1)图形绘制
plot 图表、绘图
import matplotlib.pyplot as plt
x=[1,2,3,4,5,6,7,8]
y=[3,5,6,9,13,6,32,111]
plt.xlim((0,10))
plt.ylim((0,120))
plt.xlabel('x轴',fontproperties='SimHei',fontsize=16)
plt.ylabel('y轴',fontproperties='SimHei',fontsize=16)
plt.plot(x,y,'r',lw=2)
plt.show()
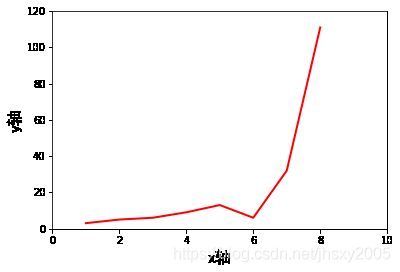
在jupyter中直接返回结果图,相比之前的海龟画图,这个是直接给结果,而海龟是弹出以python进程的窗口,名为python turtle graphics的窗口实现的动态绘图
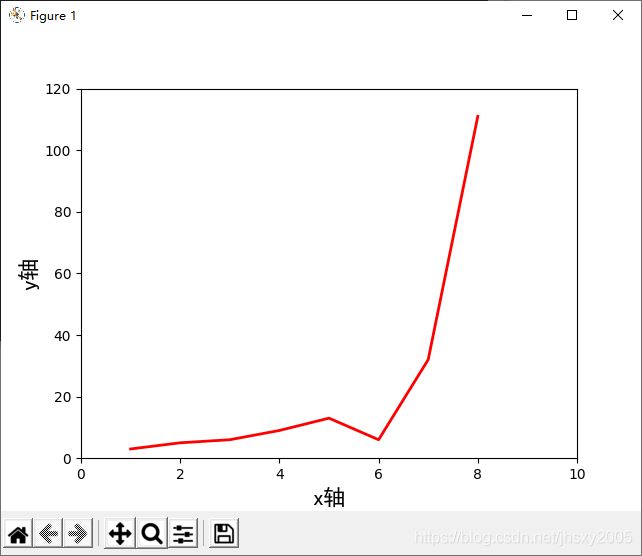
但是直接执行.py,他同样是python进程的窗口,不过是叫figure 1,且能拖动、放大等操作!figure 多个窗口,多个图形
import numpy as np
import matplotlib.pyplot as plt
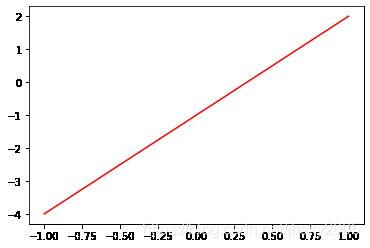
x=np.linspace(-1,1,50) # 生成50个从-1到1的均匀的数 (start,end,count) [s,e]
# figure 1
y1=3*x-1
plt.figure()
plt.plot(x,y1,'r')
# figure 2
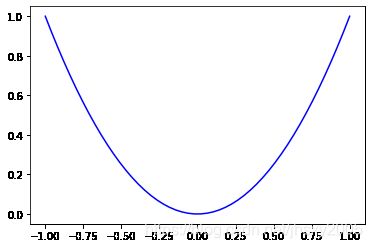
y2=x**2
plt.figure()
plt.plot(x,y2,'b')
plt.show() # 若不写,则不会显示图形窗口
array([-1. , - 0.95918367, -0.91836735, -0.87755102, -0.83673469,
-0.79591837, - 0.75510204, -0.71428571, -0.67346939, -0.63265306,
-0.59183673, - 0.55102041, -0.51020408, -0.46938776, -0.42857143,
-0.3877551 , - 0.34693878, -0.30612245, -0.26530612, -0.2244898 ,
-0.18367347, - 0.14285714, -0.10204082, -0.06122449, -0.02040816,
0.02040816, 0.06122449, 0.10204082, 0.14285714, 0.18367347,
0.2244898 , 0.26530612, 0.30612245, 0.34693878, 0.3877551 ,
0.42857143, 0.46938776, 0.51020408, 0.55102041, 0.59183673,
0.63265306, 0.67346939, 0.71428571, 0.75510204, 0.79591837,
0.83673469, 0.87755102, 0.91836735, 0.95918367, 1. ])
jupyter就算没有show也是会显示结果的,但这个结果不知道是否是jupyter的内置功能,即其实并未绘图,而是jupyter自动掉用了绘图并显示。for i in range(10):
plt.figure()
plt.plot(x,y1,'r')
print(time.time()-ss)
0.16590213775634766
但是在.py运行,很明显的感觉到耗时
2.467944860458374
肯定做了较大的运算,于是jupyter应该是把已有的运算结果直接搬了出来,而非强制运算,这方面在通常变量很好理解,但是在这种绘图结果,只能进行运算后才能切身感受!
而且他加载的直接是data:image/png;base64,iVBORw0K…U5ErkJggg==
也就是image的data,而非image路径,代码保存大小和图像大小一致,至于给我个这东西,不利用浏览器保存功能,怎么复建成一个png图片,我不知道设置图例
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(1,20,1) # [1,20)的整数
plt.plot(x,x**2+1,'red',lw=2) # 绘制线1
plt.plot(x,x*16,'b',linestyle='dashed',lw=2) # 绘制线2 这里没有上面那个代码的figure,于是两条线出现在一条图中
plt.legend(['x**2','16*x']) # 添加说明
plt.show()
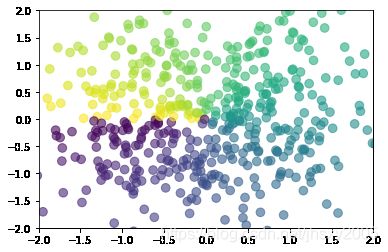
scatter 绘制散点图
import numpy as np,matplotlib.pyplot as plt
n=512
x=np.random.normal(0,1,n) # 已0为中心,离散度是1的n个数值
y=np.random.normal(0,1,n)
color=np.arctan2(y,x) # 反正切,在不同的角度,颜色不一样
plt.scatter(x,y,s=75,c=color,alpha=0.6) # s是散点大小,alpha是透明度
plt.xlim((-2.0,2.0))
plt.ylim((-2.0,2.0))
plt.show()
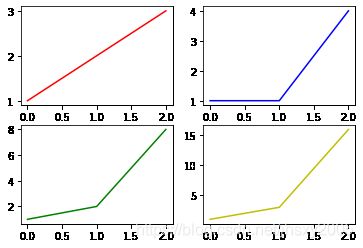
subplot 绘制多个子图
import matplotlib.pyplot as plt
plt.figure()
plt.subplot(2,2,1)
plt.plot([0,1,2],[1,2,3],'r')
plt.subplot(2,2,2)
plt.plot([0,1,2],[1,1,4],'b')
plt.subplot(2,2,3)
plt.plot([0,1,2],[1,2,8],'g')
plt.subplot(2,2,4)
plt.plot([0,1,2],[1,3,16],'y')
plt.show()
import matplotlib.pyplot as plt
plt.figure()
plt.subplot(2,2,1)
plt.plot([0,1,2],[1,2,3],'r')
plt.subplot(2,2,1)
plt.plot([0,1,2],[1,1,4],'b')
plt.subplot(2,2,4)
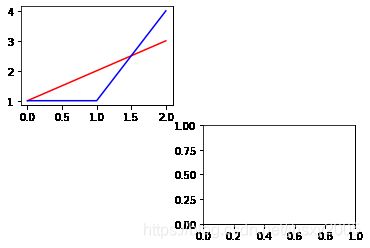
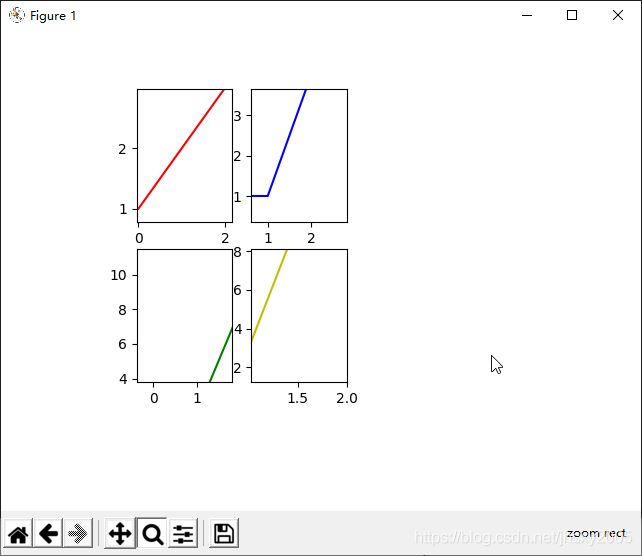
运行.py,四个图表出现在同一个窗口下,但是每个图表仍可以独立拖动和缩放,不过设置边距仍然是当做一个对象!Jieba
书中做了过多的描述,于是可以看得出,前面都是搬文档,这里是另外撰写的!分词
jieba.lcut、jieba.lcut_for_search: 返回列表
jieba.cut、jieba.icut接收3个参数
(1)string,需要分词的中文字符串,编码为Unicode、UTF-8或GBK
(2)cut_all,是否使用全模式,默认False
(3)HMM,是否使用HMM模型,默认True
jieba.cut_for_search、jieba_icut_for_search接收2个参数
(1)string
(2)HMMimport jieba
segList1=jieba.cut("居里夫人1903年获诺贝尔奖时做了精彩演讲",cut_all=True) # 338 ns
print("全模式","/".join(segList1))
segList2=jieba.cut("居里夫人1903年获诺贝尔奖时做了精彩演讲",cut_all=False) # 337 ns
print("精确模式","/".join(segList2))
#
全模式 居里/居里夫人/里夫/夫人/1903/年/获/诺贝/诺贝尔/诺贝尔奖/贝尔/奖/时/做/了/精彩/演讲
精确模式 居里夫人/1903/年/获/诺贝尔奖/时/做/了/精彩/演讲
关键词提取
jieba.analyse.extract_tags(sentence,topK=20,withWeight=False,allowPOS=())
结巴.分析.提取标签(待提取文本,权重最大的20个词,不返回关键词权重值,包括指定词性的词)import jieba
import jieba.analyse
sentence="艾萨克·牛顿(1643年1月4日——1727年3月31日)爵士,英国皇家学会会长,英国著名的物理学家,百科全书式的“全才”,著有《自然哲学的数学原理》《光学》。"
#关键词提取
keywords=jieba.analyse.extract_tags(sentence,topK=20,withWeight=True,allowPOS=('n','nr','ns'))
for item in keywords:
print(item[0],item[1])
#
艾萨克 1.5364049674375
数学原理 1.321059142725
爵士 1.13206132069
牛顿 1.03458251822375
会长 0.97365128905875
物理学家 0.97365128905875
光学 0.937137931755
英国 0.62829620167375
词性标注
jieba.posseg.POSTokenizer(tokenizer=None)import jieba.posseg as pseg
words=pseg.cut("中国人民是不可战胜的")
for word,flag in words:
print("%s %s"%(word,flag))
#
中国 ns
人民 n
是 v
不可 v
战胜 n
的 uj
for word in words:
print(word)
#
中国/ns
人民/n
是/v
不可/v
战胜/n
的/uj
Pyinstaller 打包python应用程序
书中例子只是个简单的代码,于是我把复杂的之前的plot画图打包了,应该说是编译,但是看来这个代码过于复杂,并没能运行成功而且有59.8MB!
话说现在的python已经有573MB了!
之前一个单纯的抽奖的文字代码,打包后10.3MB,正常运行!但是打开时比较慢,后面允许相对较快!
于是打开优势是没有了,不适合用来制作开袋即食的小工具!
pyinstaller -F *.py自定义模块
目录即包
pack1 pack2 main.py
A11.py A12.py A2.py场景1 同目录下调用
(1)在pack1文件夹下添加文件__init__.py ???我尝试发现这个并非一定要有
(2)分别编写源文件A11.py和模块A12中的程序代码
模块A12:# 定义函数
def func_A12():
return 'A12 in Pack1'
import A12
print(A12.func_A12())
from A12 import *
print(func_A12())
from A12 import func_A12
print(func_A12())
import A12 as a
print(a.func_A12())
from A12 import func_A12 as a
print(a())
import A12.func_A12 as a
print(a())
场景2 调用同层的子目录下
在本场景中,源文件main.py和模块A2所在的包pack2在同一路径
(1)在pack2目录下添加文件__init__.py ???这里仍没有显示出必要性
(2)分别编写模块A2和源文件main.py中的程序代码
模块A2中的程序代码:# 定义函数
def func_A2():
return 'A2 in Pack2'
from pack2.A2 import *
print(func_A2())
from pack2 import A2
print(A2.func_A2())
import pack2.A2.func_A2 as a
print(a())
import pack2
print(pack2.A2.func_A2())
pack(目录)、module(.py)、func(def)
from import
1、在导入模块的时候,第一档不能出现函数
2、不能只导入pack
import module
from pack import module
from module import func
import pack.module.func
最后一个点前必须是pack
import pack
这个pack被当做module导入了,此时没有错误,调用时错误,他无法被调用
A不能是func,最终导入不能是pack场景3 两个子目录间
import sys
sys.path.append('F:\\2019\\Documents\\python\\test\\自定义模块\\pack2')
import A2
print(A2.func_A2())
input()
import os
os.chdir("F:\\2019\\Documents\\python\\test\\自定义模块\\pack1")
import sys
sys.path.append('..\\')
import pack2.A2
print(pack2.A2.func_A2())
input()
典型案例
使用Turtle绘制表面填充正方体
收尾不必是同一点,会自动以直线连接填充,若只是花了一条线段,则不会填充
2、画笔结束时呈现封闭区域,否则报错,两个封闭区域相交处不填
3、需要设置fillcolorimport turtle
n = 100
turtle.pencolor('red')
turtle.begin_fill()
turtle.fillcolor('red')
for i in range(4):
turtle.forward(n)
turtle.left(90)
turtle.penup()
turtle.goto(50,50)
turtle.pendown()
for i in range(3):
turtle.forward(n)
turtle.right(90)
turtle.end_fill()
turtle.done()
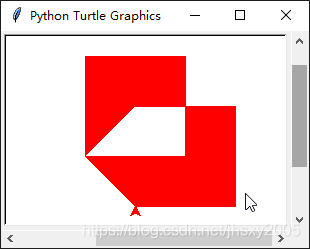
这段代码在jupyter运行时会不知名的报错一次,再运行才能画出来,直接运行.py没问题!import turtle # 导入模块
# 画正方体正面
n = 100 # 正方体边长
turtle.penup()
turtle.goto(-100,-50)
turtle.pendown()
turtle.pencolor('red')
turtle.begin_fill()
turtle.fillcolor('red')
for i in range(4):
turtle.forward(n)
turtle.left(90)
turtle.end_fill()
# 画正方体顶面
turtle.penup()
turtle.goto(-100,n-50)
turtle.pendown()
turtle.pencolor('green')
turtle.begin_fill()
turtle.fillcolor('green')
turtle.left(45)
turtle.forward(int(n*0.6))
turtle.right(45)
turtle.forward(n)
turtle.left(360-135)
turtle.forward(int(n*0.6))
turtle.end_fill()
# 画正方体右侧面
turtle.left(45)
turtle.penup()
turtle.goto(n-100,-50)
turtle.pendown()
turtle.pencolor('blue')
turtle.begin_fill()
turtle.fillcolor('blue')
turtle.left(135)
turtle.forward(int(n*0.6))
turtle.left(45)
turtle.forward(n)
turtle.left(135)
turtle.forward(int(n*0.6))
turtle.right(90)
turtle.end_fill()
turtle.done()
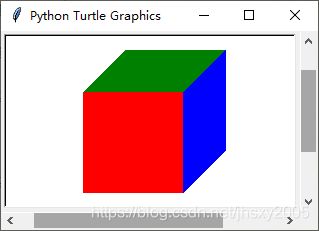
以上是书中的代码,我觉得挺烦杂的,而且这个交接点的颜色不交叉的样子import turtle as t
for i in range(50):
t.pencolor(i//10*0.2,i//10*0.2,i//10*0.2)
t.goto(0,i)
t.forward(1+0.1*i)
t.done()

turtle是支持浮点的,不过是四舍五入,而书中例子是int截断from turtle import color as c,\
forward as f,\
left as l,\
right as r,\
goto as g,\
done as d
import turtle as t
n = 100
c('red')
t.begin_fill()
t.fillcolor('red')
g(-100,0)
g(-100,-100)
g(0,-100)
g(0,0)
t.end_fill()
c('green')
t.begin_fill()
t.fillcolor('green')
g(-100,0)
l(45)
f(60)
r(45)
f(100)
t.end_fill()
c('blue')
t.begin_fill()
t.fillcolor('blue')
r(90)
f(100)
r(45)
f(60)
g(0,0)
t.end_fill()
r(90)
t.done()
使用NumPy和Matplotlib分析股票
000001在2018-07-2~2018-07-6的交易数据如下所示:
2018/7/3, 8.69, 8.7, 8.67, 8.45, 1274838.5
2018/7/4, 8.63, 8.75, 8.61, 8.61, 711153.38
2018/7/5, 8.62, 8.73, 8.6, 8.55, 835768.81
2018/7/6, 8.61, 8.78, 8.66, 8.45, 988282.75
(1)使用NumPy对骨片文件进行处理,需要先将股票交易文件000001_stock01.csv中的不同列数据分别督导多个数组中保存
(2)使用numpy.mean()计算收盘价和成交量的算术平均值
(3)使用numpy.average()函数计算收盘价的加权平均价格 加权平均=(数量1权重1+数量2权重2)/(权重1+权重2)
(4)使用numpy.max()函数、numpy.min()函数分别计算股票的最高价、最低价
(5)使用numpy.ptp()函数计算股票最高波动范围、股票最低波动范围
(6)使用matplotlib.pyplot中的相关函数绘制股票000001在2018年7月的收盘价走势图import numpy as np,os
import matplotlib.pyplot as plt
# 将000001_stock01.csv中的第4列(收盘价)、6列(成交量)数据读到数组c、v中
close,volume=np.loadtxt(os.getcwd()+'\\resource\\000001_stock01.csv',delimiter=',',usecols=(3,5),unpack=True)
print("收盘价的算术平均价格:%6.2f元"%np.mean(close))
print("成交量的算数平均值:%6.2f元"%np.mean(volume))
# 计算收盘价的加权平均价格(时间越靠近现在,权重越大)
t=np.arange(len(close))
print("收盘价的加权平均价格:%6.2f元"%(np.average(close,weights=t)))
# 你是否觉得这里很奇怪,因为没有原始数据,我是从书上抄的数据,只是一小部分
# 将000001_stock01.csv中的第3列(最高价)、第5列(最低价)数据读取到数组high、low中
high,low=np.loadtxt(".\\resource\\000001_stock01.csv",delimiter=",",usecols=(2,4),unpack=True)
print("股票最高价:%6.2f元"%np.max(high))
print("股票最低价:%6.2f元"%np.min(low))
print("股票最高价波动范围:%6.2f"%np.ptp(high))
print("股票最低价波动范围:%6.2f"%np.ptp(low))
# ptp(a, axis=None, out=None, keepdims=
成交量的算数平均值:1025112.71元
收盘价的加权平均价格: 8.63元
股票最高价: 9.05元
股票最低价: 8.45元
股票最高价波动范围: 0.35
股票最低价波动范围: 0.16

使用Pandas分析股票交易数据
Date,open,high,low,close,volume
2018/7/2, 9.05, 9.05, 8.61, 8.55, 1315520.12
2018/7/3, 8.69, 8.7, 8.67, 8.45, 1274838.5
2018/7/4, 8.63, 8.75, 8.61, 8.61, 711153.38
2018/7/5, 8.62, 8.73, 8.6, 8.55, 835768.81
2018/7/6, 8.61, 8.78, 8.66, 8.45, 988282.75
相对于NumPy,Pandas具有更方便、功能更强大的数据统计和分析方法
(1)使用Pandas中的pd.loc()函数、pd.count()函数对文件000001_stock02.csv中的股票数据进行筛选计数
(2)使用NumPy中的np.where()函数结合在Pandas中获取的列数据对股票数据进行分组
(3)调用Pandas中的pd.describe()函数对股票数据进行描述性统计
(4)调用Pandas中的pd.corr()函数分别对股票数据进行相关性分析import pandas as pd,numpy as np,os
data=pd.read_csv(os.getcwd()+'\\resource\\000001_stock02.csv')
print("1.股票最高价高于9.00元的天数:",(data.loc[data['high']>=9.00,['Date']].count()).iloc[0])
print("2.股票收盘价分组>=8.5:",np.where(data['close']>=8.5,'高','低'))
print("3.股票数据的描述性统计:")
print(data.describe())
print("4.股票数据的相关性分析:")
print(data.corr())
1.股票最高价高于9.00元的天数: 1
2.股票收盘价分组>=8.5: ['高' '低' '高' '高' '低']
3.股票数据的描述性统计:
open high low close volume
count 5.000000 5.000000 5.000000 5.000000 5.000000e+00
mean 8.720000 8.802000 8.630000 8.522000 1.025113e+06
std 0.187083 0.141669 0.032404 0.070143 2.657430e+05
min 8.610000 8.700000 8.600000 8.450000 7.111534e+05
25% 8.620000 8.730000 8.610000 8.450000 8.357688e+05
50% 8.630000 8.750000 8.610000 8.550000 9.882828e+05
75% 8.690000 8.780000 8.660000 8.550000 1.274838e+06
max 9.050000 9.050000 8.670000 8.610000 1.315520e+06
4.股票数据的相关性分析:
open high low close volume
open 1.000000 0.935716 -0.259808 0.163841 0.701911
high 0.935716 1.000000 -0.353985 0.233470 0.513434
low -0.259808 -0.353985 1.000000 -0.901938 0.436517
close 0.163841 0.233470 -0.901938 1.000000 -0.538188
volume 0.701911 0.513434 0.436517 -0.538188 1.000000
使用图像处理库处理和显示图像
(2)获取图像的数据类型和图像大小
(3)使用imageio库中的imwrite()函数等修改图像颜色、图像大小,裁剪图像。
(4)使用matplotlib.pyplt和matplotlib.image库中的相关函数绘制原始图像import imageio,os,numpy
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from PIL import Image
QB_PNG=imageio.imread('.\\resource\\QB.PNG')
print("图像的数据类型:",QB_PNG.dtype)
img_shape=QB_PNG.shape
print("图像尺寸,通道数:",QB_PNG.shape)
imageio.imwrite("QB_MC.PNG",QB_PNG*[1,0.5,0.5,1]) # 修改颜色
imageio.imwrite("QB_MS.PNG",numpy.array(Image.fromarray(QB_PNG).resize((120,70)))) # 缩放尺寸
imageio.imwrite("QB.MI.PNG",QB_PNG[600:700,600:700]) # 裁剪
plt.figure()
plt.subplot(2,2,1)
Q1=mpimg.imread("./resource/QB.png")
plt.imshow(Q1)
plt.axis('off') # 如果没有这句,背景色为白,有则按照PNG设置的透明
plt.subplot(2,2,2)
Q2=mpimg.imread('QB_MC.PNG')
plt.imshow(Q2)
plt.axis('off')
plt.subplot(2,2,3)
Q3=mpimg.imread('QB_MS.PNG')
plt.imshow(Q3)
plt.axis('off')
plt.subplot(2,2,4)
Q4=mpimg.imread('QB.MI.PNG')
plt.imshow(Q4)
plt.axis('off')
plt.show()
图像的数据类型: uint8
图像尺寸,通道数: (1319, 1313, 4)