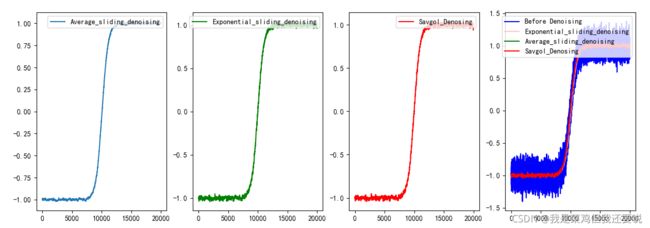
对含有奇异值和高斯噪声的数据进行处理
分别用平均滑动窗口、指数滑动窗口、SG滤波法对含有奇异值和高斯噪声的两列数据进行去奇异值和降噪,最终拟合曲线推测函数表达式。
去噪方法理论知识参考
对第一列数据:
import matplotlib.pyplot as plt
import numpy as np
from scipy import optimize
import scipy.io as scio
%matplotlib
#防止中文乱码
plt.rcParams["font.sans-serif"] = ["Simhei"]
plt.rcParams["axes.unicode_minus"] = False
data = scio.loadmat('2 data_preprocess_practice.mat')
yy3 = data["yy3"]
x = np.arange(0, 20001, 1)
#去除奇异值
def Noise_reduction(data_col) :
lst = []
i = 0
#此处用的是3sigema的方法
while i + 12 < 20001 :
lst1 = data_col[i : i + 12]
mean = np.mean(lst1)
std = np.std(lst1)
for value in lst1 :
if (value - mean) >= -3 * std and (value - mean) <= 3 * std :
lst.append(value)
i += 12
lst1 = []
return lst
#平均滑动去噪
#滑动平均法适用于,噪声的均值为0,真实值变化不大或线性变化的场景
def Average_sliding_denoising(arr, window_size) :
#对数组进首尾扩展,以滑动窗口可以处理到首尾点,思想与图片滤波算子相似
New_arr = arr[ : ]
window_size = (window_size - 1) // 2
for step in range(window_size) :
arr.insert(step, sum(arr[ : window_size]) / window_size)
arr.insert(len(arr) - step, sum(arr[len(arr) - window_size : len(arr)]) / window_size)
for i in range(window_size, len(arr) - window_size) :
New_arr[i - window_size] = (sum(arr[i - window_size : i + window_size + 1])) / (2 * window_size + 1)
return New_arr
#指数平均滑动去噪
#当误差不受观测值大小影响的话,指数滑动平均比滑动平均好;当误差随观测值大小变化时,滑动平均比指数滑动平均更好。
def Exponential_sliding_denoising(arr, weight = 0.01) :
for i in range(1, len(arr)) :
arr[i] = weight * arr[i] + (1 - weight) * arr[i - 1]
return arr
#Savitzky-Golay平滑去噪
#SG滤波法对于数据的观测信息保持的更好,在一些注重数据变化的场合会比较适用。
def create_x(size, rank):
x = []
for i in range(2 * size + 1):
m = i - size
row = [m ** j for j in range(rank)]
x.append(row)
x = np.mat(x)
return x
def Savgol_Denosing(arr, window_size, rank) :
New_arr = arr[ : ]
m = (window_size - 1) // 2
# 处理边缘数据,用边缘值首尾增加m个首尾项
for step in range(m) :
arr.insert(step, arr[0])
arr.insert(len(arr) - step, arr[len(arr) - 1])
# 创建X矩阵
X = create_x(m, rank)
# 计算加权系数矩阵B
B = (X * (X.T * X).I) * X.T
#只用更新第m个点,因此只需取B系数矩阵的第m行即可
A0 = B[m].T
# 计算平滑修正后的值
narr = []
for i in range(len(New_arr)):
y = [arr[i + j] for j in range(window_size)]
y1 = np.mat(y) * A0
y1 = float(y1)
narr.append(y1)
return narr
#可视化不同去噪方法的效果
def Mapping(lst, arr, arr1, arr2) :
x = np.array(list(range(0, len(arr), 1)))
fig = plt.figure(figsize=(15, 5))
fig.set(alpha = 0.2)
plt.subplot2grid((1,4), (0, 0))
plt.plot(x, arr, label = 'Average_sliding_denoising')
plt.legend(loc = 1)
plt.subplot2grid((1, 4), (0, 1))
plt.plot(x, arr1, 'g-', label = 'Exponential_sliding_denoising')
plt.legend(loc = 1)
plt.subplot2grid((1, 4), (0, 2))
plt.plot(x, arr2, 'r-', label = 'Savgol_Denosing')
plt.legend(loc = 1)
plt.subplot2grid((1, 4), (0, 3))
plt.plot(x, lst, 'b-', x, arr, 'pink', x, arr1, 'g', x, arr2, 'r')
plt.legend(['Before Denoising', 'Exponential_sliding_denoising', 'Average_sliding_denoising', 'Savgol_Denosing'], loc = 1)
plt.show()
#小结,单纯从可视化效果来看,指数平均化动的效果是最好的
#数据重新拟合,推测函数
def Polynomial_fitting(lst) :
x1 = np.arange(0, len(lst), 1).astype(float)
z1 = np.polyfit(x1, lst, 11)
# print(np.poly1d(z1))
x_points = np.linspace(0, 19973, 19973)
y_point = np.polyval(z1, x_points)
fig1 = plt.figure()
plt.plot(x1, lst, x_points, y_point, 'r')
plt.legend(['Before fitting', 'After fitting'], loc = 1)
plt.show()
data_col1 = []
data_col2 = []
for line in yy3 :
data_col1.append(line[0])
data_col2.append(line[1])
data_col1 = np.array(data_col1)
data_col2 = np.array(data_col2)
lst1 = Noise_reduction(data_col1)
lst1_A = Average_sliding_denoising(Noise_reduction(data_col1), 61)
lst1_E = Exponential_sliding_denoising(Noise_reduction(data_col1))
lst1_S = Savgol_Denosing(Noise_reduction(data_col1), 59, 2)
Mapping(lst1, lst1_A, lst1_E, lst1_S)
Polynomial_fitting1(lst1_A)
对第二列数据:
def Polynomial_fitting2(lst) :
x1 = np.arange(0, len(lst), 1).astype(float)
z1 = np.polyfit(x1, lst, 50)
x_points = np.linspace(0, 19973, 19973)
y_point = np.polyval(z1, x_points)
fig1 = plt.figure()
plt.plot(x1, lst, x_points, y_point, 'r')
plt.legend(['Before fitting', 'After fitting'], loc = 1)
plt.show()
lst2 = Noise_reduction(data_col2)
lst2_A = Average_sliding_denoising(Noise_reduction(data_col2), 61)
lst2_E = Exponential_sliding_denoising(Noise_reduction(data_col2))
lst2_S = Savgol_Denosing(Noise_reduction(data_col2), 59, 2)
Mapping(lst2, lst2_E, lst2_A, lst2_S)
Polynomial_fitting2(lst2_A)