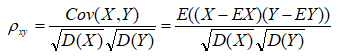样本相似度度量

样本相似度度量

分类时，有时需要估算样本之间的相似度，这时候就需要进行相似度度量。
常见的相似度度量有以下几种：

欧氏距离

两个样本a(x₁₁, x₁₂, x₁₃, … ,x_1n)和b(x₂₁, x₂₂, x₂₃, x_2n)的欧氏距离：

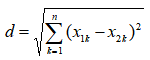
欧氏距离基于各维度特征的绝对数值，因此欧氏距离需要保证各维度指标在相同的刻度级别

标准化欧氏距离

标准欧氏距离是针对欧氏距离的缺点而作的一种改进。
其基本思路为：将原特征值转化为新的特征值，新特征值满足均值为0，方差为1，即：

这里x表示的是原特征，m表示的是原特征的均值，s表示原特征的标准差。
得到标准化欧氏距离计算公式：

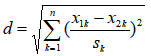
如果将方差的倒数看成是一个权重，则该公式可以看成是一种加权欧氏距离。

曼哈顿距离

曼哈顿距离也叫做城市街区距离(city block)。
(1) 二维平面上两点a(x₁,y₁)和b(x₂,y₂)的曼哈顿距离：

(2) n维向量a(x₁₁,x₁₂,…x_1n)和b(x₂₁,x₂₂,…,x_2n)的曼哈顿距离：

切比雪夫距离

切比雪夫距离是(x₁,y₁)到(x₂,y₂)的横/纵坐标的最大值。
两个n维样本a(x₁₁,x₁₂,…,x_1n)和b(x₂₁,x₂₂,…x_2n)的切比雪夫距离：

等价于：

闵可夫斯基距离

两个n维样本a(x₁₁,x₁₂,…,x_1n)和b(x₂₁,x₂₂,…x_2n)的闵可夫斯基距离为：

(1) 当p = 1时，就是曼哈顿距离
(2) 当p = 2时，就是欧氏距离
(3) 当p ->∞时，就是切比雪夫距离

欧氏距离、曼哈顿距离、切比雪夫距离和闵科夫斯基距离的缺点：
(1) 将各个特征的量纲（也就是单位）等同的看待了，但如：“10kg”和“10m”难道是等价的吗？
(2) 没有考虑各个分量的分布（期望、方差等）可能是不同的。

马氏距离

两个服从同一分布且其协方差矩阵为Σ的随机变量x和y的差异程度。

目的： 计算两个样本间距离时，需要考虑样本所在分布的影响，包括以下两个方面：
a) 不同维度上的方差不同，进而不同维度在计算距离时的重要性不同。
b) 不同维度之间可能存在相关性，干扰距离。
当数据分布已知时：通常用马氏距离代替欧氏距离，或对数据进行转换（比如PCA）

性质： 马氏距离消除了样本不同维度之间的方差差异和相关性，是一个无量纲的度量方式。

马氏距离与欧氏距离的关系
(1)、协方差是单位矩阵时，样本特征维度之间的相关性（协方差）为0，量纲一致，此时的马氏距离=欧氏距离
(2)、协方差矩阵是对角矩阵时，样本特征维度之间的量纲一致，此时的马氏距离=标准化欧氏距离。

夹角余弦

对于两个n维样本点a(x₁₁,x₁₂,x₁₃,…,x_1n)和b(x₂₁,x₂₂,…x_2n)可使用余弦公式：

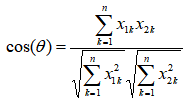
夹角余弦范围为[-1,1]，余弦值和夹角成反比，和相似度成正比
夹角余弦越大----->两个向量的夹角越小----->相似度越大
夹角余弦越小---->两个向量的夹角越大------->相似度越小

汉明距离

两个等长字符串的s1和s2之间的汉明距离定义为将其中一个变为另外一个所需作的最小替换次数，例如，“1111”和“1001”之间的汉明距离为2。
应用：信息编码（为了增强容错性，使得编码之间的最小汉明距离尽可能大）。

杰卡德距离 & 杰拉德相似系数

杰卡德相似系数
集合A和集合B的交集元素在A，B并集中所占的比例，称为两个集合的杰卡德相似系数。

杰卡德相似系数是衡量两个集合的相似度的一种指标。

杰卡德距离
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。

杰卡德相似系数与杰卡德距离的应用

1.杰卡德相似系数可用于衡量样本的相似度。
如，A(0,1,1,1)，B(1,0,1,1)将样本看成一个集合，1表示集合包含该元素，0表示集合不包含该元素。
p:样本A与B都是1的维度的个数
q:样本A是1，B是0的维度的个数
r：样本A是0，B是1的维度的个数
s：样本A与B都是0的维度的个数
那么A和B的杰卡德相似系数：

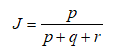
为什么分母不加s呢？
对于杰卡德相似系数或杰卡德距离来说，它处理的都是非对称变量（即状态的两个输出不是同等重要的）。例如：疾病检查的阳性和阴性结果，负匹配的数量s被认为是不重要的，可在计算时忽略。

2.举例
考察两个患者的症状情况（发烧，咳嗽，白细胞升高，呕吐，流鼻涕），如果他们的取值分别为(1,1,0,0,1)和(1,0,0,1,0)，则它们的杰卡德距离为(2+1)/(1+2+1)=3/4，表示两者的相异度，而1-3/4 = 1/4表示两者的相异度。

在CTR指标上，Jaccard的推荐精准度远优于cosine。

相关系数 & 相关距离

1. 相关系数的定义
   
   衡量随机变量x与Y相关程度的一种方法，取值范围为[-1,1]，绝对值越大，X与Y的相关度越高，ρ>0表示正相关，ρ<0表示负相关。

2. 相关距离
   

欧氏距离和余弦相似度

1. 欧氏距离：反映个体数值特征的差异，用于需要从维度的数值大小中体现差异的分析，例如使用用户行为指标分析用户价值的相似度问题。
2. 余弦相似度：从方向上区分差异，对绝对数值不敏感，用于使用用户对内容评分来区别用户兴趣的相似度差异（修正用户之间可能存在的度量标准不同意的问题）。

欧氏距离：分析程度
标准欧氏距离：分析程度和倾向
余弦相似度：分析倾向