Python语言实现基于组平均的AGNES算法，支持多维数组，距离用欧式距离

---

前言

题目要求：

• 任选语言（本文选择Python）自实现基于组平均的AGNES算法
• 支持多维数组
• 采用欧氏距离

先上效果图，（项目链接在文章最后）：

---

提示：以下是本篇文章正文内容

一、关于算法的相关介绍

AGNES(Agglomerative Nesting)是一种典型的凝聚型层次聚类算法

层次聚类、组平均

• 层次聚类方法是古老而且常用的聚类方法。
• 层次聚类方法又有以下两种产生层次聚类的基本方法。

1. 凝聚的：该方法是自底向上的方法，初始每个对象看做一个簇，每一步合并最相近的簇，最终形成一个簇。
2. 分类的：该方法是自顶向下的方法，从包含的所有点的簇开始，每一步分裂一个簇，知道仅剩下单点的簇。

在凝聚的层次聚类方法中，需要定义簇之间的相近性。
有许多凝聚层次的聚类技术，如单链、全链、组平均，本文介绍组平均。

组平均中两个簇的邻近度定义为两个不同簇中任意两点之间的平均距离。

两个簇之间的相似度计算公式为：
dist({m1,m2},{m3,m4})=(dist(m1,m3)+dist(m1,m4)+dist(m2,m3)+dist(m2,m4))/4

本题算法中心逻辑

如果簇C1中的一个对象和簇C2中的一个对象之间的距离是所有属于不同簇的对象间欧式距离中最小的，C1和C2被合并。基于组平均方法，其每个簇可以被簇中的所有对象代表，两个簇之间的相似度由这两个簇的邻近度来确定。

伪代码：

data = n个m维的数据
dis = m*m的矩阵，初始值为0  # dis[i][j] 表示簇i和簇j之间的距离(0 <= i 
pre_target = []  # len(pre_target) = m

# 第一步：初始化数据
dis[j][i] = ((data.iloc[j] - data.iloc[i]) ** 2).sum()
# 将对角线元素设置为无穷大
# 由于每次选取的是矩阵中的最小值，故dis[i][j]=MAX保证簇i和簇j之后不再参与运算
dis[np.diag_indices_from(dis)] = MAX

# 第二步：遍历数据
while 循环:
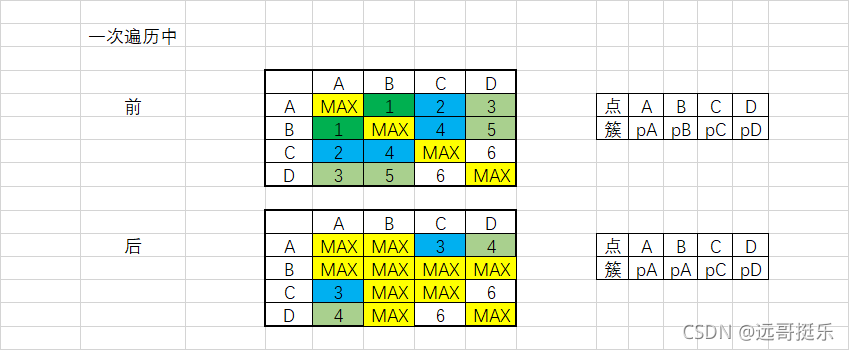
	# 找到矩阵中最小值的位置，找出此轮遍历中应该合并的两个点所在的簇pA和pB
	pA, pB = divmod(dis.argmin(), dis.shape[1])
	# 重点！！！
	"""
	1. dis[:, pA]表示各簇到簇pA的距离，dis[:, pB]表示各簇到簇pB的距离，故(dis[:, pA] + dis[:, pB]) / 2表示将pA和pB合并之后各簇到新簇
	2. 由于矩阵为对称矩阵，故dis[:, pA] == dis[pA]，dis[:, pB] == dis[pB]，两者等号两边必须同时修改，下面将不再重复强调
	"""
	# 将新平均距离赋给pA，作为新的各簇到新簇pApB的值
	dis[:, pA] = (dis[:, pA] + dis[:, pB]) / 2
	dis[pA] = dis[:, pA]
	# pB簇置为最大，之后再不参与计算，理由同第一步中附最大值
	dis[:, pB] = MAX
	dis[pB] = MAX
	# 将B所在pB簇所有点全部赋上点A所在的簇序号值
	pre_target[np.where(pre_target == pB)] = pA

	# 跳出条件本处设定为直到m个簇被合并最终变成k个簇，k为自己设定的值
	if 满足条件:
		break

二、核心内容

1、数据集介绍

提供三个测试数据集

链接：https://pan.baidu.com/s/1P4IRqy5yX7zUnBeR6_ryJA
提取码：ygtl

文件命名为：cluster_x-y_z.csv
其中各参数表示一共有x个y维的数据需要聚为z个类

比如： cluster_500-10_7.csv 表示 500个初始点，特征量有10维，需要聚为7个类。数据集中，target为聚类目标量，可用来后期校验结果正确性

2、核心代码

import numpy as np
import pandas as pd

import time
start = time.time()

# 读取数据
read_df = pd.read_csv('../../datas/cluster_500-10_7.csv')

target = read_df.iloc[:, -1]
data = read_df.iloc[:, 1:-1]

k = 7
n = data.shape[0]
dis = np.zeros([n, n])
pre_target = np.arange(n)

# 初始化dis矩阵
# 求两两簇（点）之间的距离
for i in range(n-1):
    for j in range(i+1, n):
        dis[j][i] = ((data.iloc[j] - data.iloc[i]) ** 2).sum()
    print("初始化dis矩阵进度：{}/{}".format(i+1, n))
# 下三角复制到上三角
i_lower = np.triu_indices(n, 0)
dis[i_lower] = dis.T[i_lower]
# 无穷大为最大值
MAX = float('inf')
# 对角线附上最大值不参与运算
dis[np.diag_indices_from(dis)] = MAX
print("初始化dis矩阵进度：{}/{}".format(n, n))

_iter = 1

print("开始循环迭代")

while _iter <= n:
    # 找出最距离最小的两个点
    pA, pB = divmod(dis.argmin(), dis.shape[1])
    # 将新平均距离赋给pA，作为新的各簇到新簇pApB的值
    dis[:, pA] = (dis[:, pA] + dis[:, pB]) / 2
    dis[pA] = dis[:, pA]
    # pB簇置为最大
    dis[:, pB] = MAX
    dis[pB] = MAX
    # 将B所在pB簇所有点全部赋上点A所在的簇序号值
    pre_target[np.where(pre_target == pB)] = pA
    # 簇数
    c_num = len(np.unique(pre_target))
    if _iter % 10 == 0:
        print("循环迭代次数：{}，此时有{}个簇".format(_iter, c_num))
    # 循环直至分成k簇
    if c_num == k:
        break
    _iter += 1
    
print("结束循环迭代")

#pca降维
from sklearn.decomposition import PCA

pca = PCA(n_components=2)
newData = pca.fit_transform(data)
newData = pd.DataFrame(newData)

# 可视化
import matplotlib.pyplot as plt
x = np.array(newData.iloc[:, 0])
y = np.array(newData.iloc[:, 1])

# 原数据
plt.subplot(2,1,1)
plt.scatter(x, y, c=np.array(target))
# 预测数据
plt.subplot(2,1,2)
plt.scatter(x, y, c=pre_target)
plt.show()

end = time.time()
print(end-start)

运行结果截图：

500*10的数据集一分钟左右就能完成，效率还挺高的

3、完整项目

对核心代码做“亿点点”的改造和包装之后就做成了文章开头的样子，截图如下：

项目完整代码下载链接：

点击跳转

---

结语

创作不易，如果您觉得写得还行，还请点赞、评论、收藏走一波。