PythonCV学习记录9——霍夫变换
目录
零之前言
一.霍夫变换原理简述
二.霍夫直线检测
1.基础检测
2.优化检测
三.霍夫圆环检测
零之前言
百度百科解释道:
霍夫变换是一种特征检测(feature extraction),被广泛应用在图像分析(image analysis)、计算机视觉(computer vision)以及数位影像处理(digital image processing)。霍夫变换是用来辨别找出物件中的特征,例如:线条。他的算法流程大致如下,给定一个物件、要辨别的形状的种类,算法会在参数空间(parameter space)中执行投票来决定物体的形状,而这是由累加空间(accumulator space)里的局部最大值(local maximum)来决定。
一.霍夫变换原理简述
个人来说,没怎么看懂怎么看懂它的变换法则,改天有机会看看源代码。目前的理解如下表示(用直线做例子吧,对于其他函数的原理也就是增加几个参数变量就可以决定的,核心思想看直线就行):
对于任意一条直线,我们可以表示为:![]() 。当我们知道,如果x,y一定时,只要k,q确定一个,那么就可以确定k和q了。也就是说知三推一。但是,如果我们不知道直线的形状,也就是,k,q都不知道的情况下,我们不能确定直线,也就是说,kq两个我们都不知道,但是如果我们在一个范围内取k,那么就会得到一个范围的q,那么k,q就能组成一个函数。这个函数代表着过该点的在取值范围内的所有直线,比如我们假设
。当我们知道,如果x,y一定时,只要k,q确定一个,那么就可以确定k和q了。也就是说知三推一。但是,如果我们不知道直线的形状,也就是,k,q都不知道的情况下,我们不能确定直线,也就是说,kq两个我们都不知道,但是如果我们在一个范围内取k,那么就会得到一个范围的q,那么k,q就能组成一个函数。这个函数代表着过该点的在取值范围内的所有直线,比如我们假设![]() ,
,![]() ,那么可能是这样的一个图:记此时的(k,h)为集合A
,那么可能是这样的一个图:记此时的(k,h)为集合A
然后,我们在(1,1)点继续这样做:
在(1.1)点一个一个试出来的(k,h)出来的集合为B
然后![]() ,说明他们中有一对共同的参数k=1,h=0。说明有一根直线都是经过了(0,0)和(1,1)的。那两点能确定一条直线,说明,这条直线就是
,说明他们中有一对共同的参数k=1,h=0。说明有一根直线都是经过了(0,0)和(1,1)的。那两点能确定一条直线,说明,这条直线就是![]() 。
。
但是,如果我们要挨个试值就很沙雕,因为![]() 。那么我们能不能给k,h一个范围呢?
。那么我们能不能给k,h一个范围呢?
答案是有的,极坐标系。对于直线,我们可以写成这样![]() 。别问我为啥和高中教材上的基本形式不一样,你自己画一画转换一下就知道了。直线的最大长度,肯定是我们图片的对角线,
。别问我为啥和高中教材上的基本形式不一样,你自己画一画转换一下就知道了。直线的最大长度,肯定是我们图片的对角线,![]() 。那么这个值就非常固定了。
。那么这个值就非常固定了。
对于直线的数量我们可以由![]() 的分度值决定。比如每次
的分度值决定。比如每次![]() 增长0.1π和1π,两者差距一下子就出来了。分度值越精确,直线的数量也就确多,也更精确,但是代码执行的时间会更长。这个由实际决定了呗。
增长0.1π和1π,两者差距一下子就出来了。分度值越精确,直线的数量也就确多,也更精确,但是代码执行的时间会更长。这个由实际决定了呗。
然后对于一幅图画,我们只要把每一个像素点都用这种方法跑一次,然后把满足的数组[ρ,θ]的值+1,这样,我们就能得到很多直线了!然后给一个阈值,要是数组[ρ,θ]大于这个阈值,那么我们就可以视为这个直线存在。
这有个大牛的文章:http://www.renrendoc.com/p-11640782.html
原理就是这样,也就是说,只要能给出参数方程,就能用该方法找到东西。
二.霍夫直线检测
1.基础检测
首先,我们必须给图像边缘检测,用canny边缘过滤下,然后就是调用
lines = cv2.HoughLines(edges,1,np.pi/360,250)第一个参数是边缘线的图。
第二个是长度的分度值,也就是1像素,可以往上改大。
第三个参数是角度的分度值,可以用π来除以一个数决定。
第四个参数是累加器值,只有超过这个阈值的,我们才视为一根直线。
然后再用数学算法把![]() 给转换成坐标和直线,就可以画出来了!这里放完整代码
给转换成坐标和直线,就可以画出来了!这里放完整代码
import cv2
import numpy as np
img = cv2.imread('line.jpg',1)
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,20,150,apertureSize = 3)
lines = cv2.HoughLinesP(edges,1,np.pi/180,1)
for rho,theta in lines[0]:
a = np.cos(theta)
b = np.sin(theta)
x0 = a*rho
y0 = b*rho
x1 = int(x0 + 1000*(-b))
y1 = int(y0 + 1000*(a))
x2 = int(x0 - 1000*(-b))
y2 = int(y0 - 1000*(a))
cv2.line(img,(x1,y1),(x2,y2),(0,0,255),1)
cv2.imshow('1',img)
cv2.waitKey(0)2.优化检测
官方解释:
从上边的过程我们可以发现:仅仅是一条直线都需要两个参数,这需要大量的计算。Probabilistic_Hough_Transform 是对霍夫变换的一种优化。它不会对每一个点都进行计算,而是从一幅图像中随机选取(是不是也可以使用图像金字塔呢?)一个点集进行计算,对于直线检测来说这已经足够了。但是使用这种变换我们必须要降低阈值(总的点数都少了,阈值肯定也要小呀!)。
lines = cv2.HoughLinesP(edges,1,np.pi/180,100,minLineLength,maxLineGap)它有额外的两个参数:
• minLineLength - 线的最短长度。比这个短的线都会被忽略。
• MaxLineGap - 两条线段之间的最大间隔,如果小于此值,这两条直线就被看成是一条直线。
更加给力的是,这个函数的返回值就是直线的起点和终点。
所以代码可以简化成这样:
import cv2
import numpy as np
img = cv2.imread('line.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
minLineLength = 100
maxLineGap = 10
lines = cv2.HoughLinesP(edges,1,np.pi/180,100,minLineLength,maxLineGap)
for x1,y1,x2,y2 in lines[0]:
cv2.line(img,(x1,y1),(x2,y2),(0,255,0),2)
cv2.imshow('1',img)
cv2.waitKey(0)三.霍夫圆环检测
原理可以同直线,只不过圆形的数学表达式为 (x − x center ) 2 +(y − y center ) 2 = r 2 ,其中(x center ,y center )为圆心的坐标,r 为圆的直径。从这个等式中我们可以看出:一个圆环需要 3个参数来确定。所以进行圆环霍夫变换的累加器必须是 3 维的,这样的话效率就会很低。所以 OpenCV 用来一个比较巧妙的办法,霍夫梯度法,它可以使用边界的梯度信息。所以直接看下图:
这是官方代码
import cv2
import numpy as np
img = cv2.imread('circle.jpg',0)
img = cv2.medianBlur(img,5)
cimg = cv2.cvtColor(img,cv2.COLOR_GRAY2BGR)
circles = cv2.HoughCircles(img,cv2.HOUGH_GRADIENT,1,200,param1=50,param2=30,minRadius=0,maxRadius=0)
circles = np.uint16(np.around(circles))
for i in circles[0,:]:
# draw the outer circle
cv2.circle(cimg,(i[0],i[1]),i[2],(0,255,0),2)
# draw the center of the circle
cv2.circle(cimg,(i[0],i[1]),2,(0,0,255),3)
cv2.imshow('detected circles',cimg)
cv2.waitKey(0)
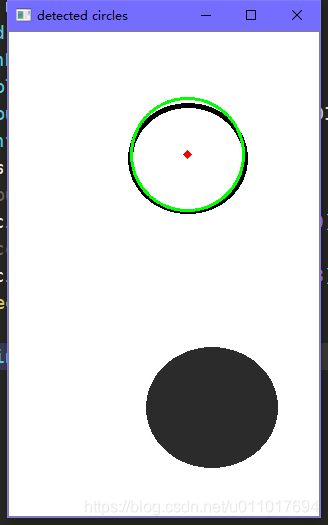
cv2.destroyAllWindows()效果:
如果我们加一个边缘检测后就这个样子:
我也不知道这个圆的差距为什么这样大...
更改下
circles = cv2.HoughCircles(edges,cv2.HOUGH_GRADIENT,1,150,param1=40,param2=25,minRadius=0,maxRadius=0)param1和param2的值修改后,拟合得非常好。
差不多至此,霍夫变换的东西就差不多了。