BOBCAT: 基于双层优化的计算机化自适应测验（超硬核解读论文+阅读论文技巧）

前言

大家好，我是小曾，今天主要给大家分享一篇最近看到的一篇文章
BOBCAT: Bilevel Optimization-Based Computerized Adaptive Testing
下载链接：https://arxiv.org/pdf/2108.07386.pdf
这篇文章是由Aritra Ghosh and Andrew Lan 在8月份发表在2021年IJCAI会议上的
希望我的分享能够为看到的小伙伴们提供帮助，加深理解！

Abstract

看一篇论文 第一步都是看摘要，一篇文章值不值得看，通过摘要就能够窥探一二，如果能够勾起你的兴趣，那么这篇文章你会主动的读下去。正如你认识朋友的时候，首先得第一印象很重要，如果印象好，才会继续沟通交流下去。

CAT简介：计算机自适应测试 (CAT) 是指一种针对每个学生/考生进行个性化的测试形式。CAT 方法根据每个学生对之前问题的回答，自适应地为每个学生选择下一个信息量最大的问题/项目，有效地缩短了测试时间。
现有方法：现有的 CAT 方法使用项目反应理论 (IRT) 模型将学生的能力与他们对问题的反应联系起来，以及旨在尽快减少能力估计误差的静态问题选择算法；
现有方法不足：这些算法无法通过从大规模学生反应数据中学习来改进。
本文贡献：
1、在本文中，我们提出了 BOBCAT，一种基于双层优化的 CAT 框架，可直接从训练数据中学习数据驱动的问题选择算法。
2、BOBCAT 与潜在的学生反应模型无关，并且在自适应测试过程中具有计算效率。
3、通过对五个真实世界学生反应数据集的大量实验，我们表明 BOBCAT 在减少测试长度方面优于现有的 CAT 方法（有时显着）。

Introduction

下面来介绍文章的相关内容背景

CAT 介绍

CAT简介：通过使用一种算法，根据学生对先前问题的回答，自适应地为每个学生选择下一个问题。
CAT目标:更快更准的测试学生的能力
CAT组成 ：认知诊断模型、候选题库、选题算法

传统的认知诊断模型

最简单的形式：Yi,j = 1是学生i对问题j的二值回答，其中1表示正确答案，σ(·)表示Sigmoid/Logistic函数，θi∈R , bj∈R分别对应于学生的能力和问题的难度
$$p\left(Y_{i,j}=1\right)=\sigma \left({\theta }_i-b_j\right)$$
最直观的理解就是学生的能力与题目难度的差值，经过sigmoid后代表答对的概率，所以说学生的能力越大，那么答对的概率也就越大。
还有一种变体形式，增加了猜测度和区分度两个参数，描述学生能力会更准确：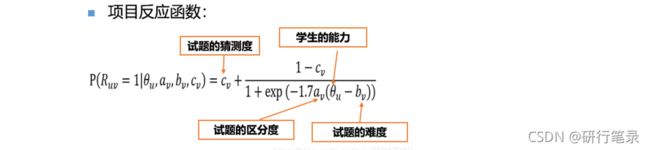

传统的CAT选题策略

最大Fisher信息量：选择信息量最大的问题，使学生特征测量误差最小化
$$j_i^{(t)}={\mathrm{argmax}}_{j\in {\Omega }_i^{(t)}}{I}_j\left({\hat{\theta }}_i^{(t-1)}\right)$$
${\hat{\theta }}_i^{(t-1)}$ 代表根据之前的选题学生回答的能力表示
Ij 代表选择第j道题目的信息量

传统方法局限性

1. 大多数问题选择算法都是专门为IRT模型设计的，捕捉复杂学生问题交互的能力受到限制
2. 大多数现有的问题选择算法是静态的，因为它们需要预定义的信息量度量。【它们只能使用大规模的学生回答数据来改进底层的IRT模型(例如，校准问题难度参数)，而不是问题选择算法。】

Contributions

这块基本上就是传统方法的局限性或者不足，加以改进，成为整篇文章的Motivation

1、将CAT重塑为一个双层优化问题，提出基于双层优化的CAT框架，直接学习数据驱动的问题选择算法。
【CAT构建双层优化问题细节：在外部发展最优化问题中，我们通过显式地最大化学生在待定元问题集中回答的预测可能性，学习了反应模型参数和数据驱动的问题选择算法；在内部发展最优化问题中，我们通过最大化每个学生在观察到的训练问题集中反应的预测可能性，使外层反应模型适用于每个学生；该双层优化框架通过训练元设置，直接学习有效、高效的问题选择算法。问题选择算法就会直接从过去的问题回答中选择下一个问题，而不需要在CAT过程中实时重复估计学生参数】

2、我们采用了梯度的近似估计器。双层优化问题中的问题选择算法参数。这种近似利用了每个问题对算法参数的影响来降低梯度估计中的方差，并导致比无偏梯度估计器更好的问题选择算法

3、通过在五个大规模的真实世界的学生回答数据集上进行大量的定量和定性实验，验证了Bobcat的有效性

强调：学习数据驱动的问题选择算法，而不是开发最好的底层学生响应模型。

BOBCAT框架

相信刚刚在贡献里面提到双层优化，有很多人是不太了解的，所以在介绍BOBCAT框架之前，先介绍一下双层优化问题，然后再介绍框架。
其实我们看文章的时候，有时文章所提到的技术或者算法，不太了解的时候，我们要有一个刨根问底的求知欲，立马就要进行灌注、给自己的知识储备库充电。

双层优化问题

双层优化（Bilevel optimization problem）针对的是一个目标函数，在前一个优化方向的结果中再进行另一个方向的优化。

可以看到上述公式：F代表外部优化问题的目标函数，L代表内部优化问题的目标函数，我们的最终目标是，既要F最小，同时L也是最小的。
具体优化过程：首先是内部目标函数在训练集中不断优化内部变量，然后外部目标函数在验证集样本中不断优化外部变量。

BOBCAT框架

首先看一下这个图片：主要介绍了Bobcat的框架，分为两个部分，Train Question 和 Meta Question Set 分别对应的是训练集和验证集。

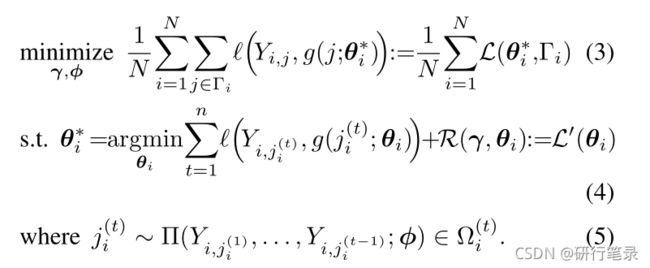
整个过程都是根据上面3、4、5公式来进行展开，其中介绍一下重要参数

γ：全局响应模型参数 φ：问题选择算法参数 θ∗i是全局参数γ和φ的函数

下面我们来跟着图中箭头方向来了解一下整体过程，
1、首先我们在训练集里面通过公式5，输入的是用户题目以及回答记录，通过问题选择算法选择出下一道要选择的题目j，也就是图中的Q4
2、输入Q4题目后，经过g（·）全局认知诊断模型以及学生i当前的学生能力，可以得到j的预测结果，以及训练集中真实的学生label(Yi,j)，计算出损失函数
3、其中公式4对应的R代表的是正则化，惩罚局部参数与其全局值的较大偏差，直到得到最小值更新后的θ∗i 【相当于内部优化完成】
4、可以看到蓝框部分，公式3，在验证集(Meta Question Set)里，根据内部传到外部的参数 θ∗i，通过g（·）全局认知诊断模型，计算出二元交叉熵损失，得到每个学生在元问题集中回答的问题的损失总和，更新全局参数γ 和 问题选择算法参数φ。

通过这个框架，也许会有疑问，为什么这样训练的问题选择算法参数会对选题比较好呢？

其实可以反向思维理解，对于一个用户而言，我在公式5 的时候给你选择最适合的题目(相当于)，那么对应公式4这块，无论这个用户答对答错记录，我这个模型判断你对错就是比较准的，因此loss也就最小，那么这个能力再传输到外层，对应的模型参数和能力在验证集里面也是准确的，因此所得到的loss也是最小的。

这也就证明，如果我参数优化的好，那么根据这个公式，也能选择好的题目、

BOBCAT 训练过程

具体流程：

对于上面的伪代码，那么跟着小曾来继续回顾一遍BOBCAT训练过程
1、一开始初始化全局参数γ，φ、学习率η1、η2、α和内层的GD步数K
2、随机选择部分学生记录分成训练集和验证集
3、根据学生对以前选择的问题的回答，对学生的当前状态(T)进行编码
4、通过问题选择算法选出题目J
5、通过梯度下降不断优化参数θ∗i
6、使用公式来估计梯度
7、更新选择题目算法的参数
8、在外层优化中，来更新全局模型的参数

最后直到收敛即可

Optimization

使用梯度下降(GD)来解决局部响应模型参数θ∗I的内层优化问题

通过从γ中采取K个GD步骤来使本地学生特定的参数偏离全局响应模型参数，其中每个步骤如下所示：$${\mathbf{\theta }}_i\leftarrow {\mathbf{\theta }}_i-{\alpha {\nabla }_{\mathbf{\theta }}\sum _{t=1}^n\ell \left(Y_{i,j_i^{(t)}},g\left(j_i^{(t)};\mathbf{\theta }\right)\right)|}_{{\mathbf{\theta }}_i}$$
α是学习速率，全局参数γ要求我们计算梯度w.r.t

为了学习选择算法参数φ，我们需要通过学生特定的参数θ∗I(γ，φ)来计算(3)w.r.t.中外层目标的梯度（即内层优化问题的解）

单个学生的梯度(所有学生的全部梯度和)由下式给出
$${\nabla }_{\varphi }\mathcal{L}\left({\mathbf{\theta }}_i^{\ast }(\gamma ,\varphi ),{\Gamma }_i\right)={\nabla }_{\varphi }{\mathbb{E}}_{j_i^{(1:n)}\sim \Pi (\cdot ;\varphi )}\left[\mathcal{L}\left({\mathbf{\theta }}_i^{\ast }\left(\gamma ,\left\{j_i^{(1:n)}\right\}\right),{\Gamma }_i\right)\right]$$

离散性质不可微，无法计算精确梯度

梯度估计的方法

无偏梯度估计(Unbiased Gradient Estimate)

使用基于得分函数的恒等式 (∂logf(X;φ)/∂φ=(∂f(X;φ)/∂φ)/f(X;φ)

任意概率分布f(X；φ))估计(7)中的无偏梯度为$$\begin{array}{rl}& {\nabla }_{\varphi }{\mathbb{E}}_{j_i^{(1:n)}\sim \Pi (\cdot ;\varphi )}\left[\mathcal{L}\left({\mathbf{\theta }}_i^{\ast }\left(\mathbf{\gamma },\left\{j_i^{(1:n)}\right\}\right),{\Gamma }_i\right)\right]\\ =& {\mathbb{E}}_{j_i^{(1:n)}\sim \Pi (\cdot ;\varphi )}\left[\left(\mathcal{L}\left({\mathbf{\theta }}_i^{\ast },{\Gamma }_i\right)-b_i\right){\nabla }_{\varphi }\log \prod _{t=1}^n\Pi \left(j_i^{(t)}\mid {\mathbf{x}}_i^{(t)};\mathbf{\varphi }\right)\right]\\ =& {\mathbb{E}}_{j_i^{(1:n)}\sim \Pi (\cdot ;\varphi )}\left[\left(\mathcal{L}\left({\mathbf{\theta }}_i^{\ast },{\Gamma }_i\right)-b_i\right)\sum _{t=1}^n{\nabla }_{\varphi }\log \Pi \left(j_i^{(t)}\mid {\mathbf{x}}_i^{(t)};\varphi \right)\right]\end{array}$$
其中bi是一个控制变量，用于减少梯度估计的方差。这种无偏梯度类似于CA T的强化学习型算法，这一想法在[Nurakhmetov，2019]中讨论过

这种无偏梯度估计只通过选择的问题来更新问题选择算法的参数，而没有包括对可用的但没有选择的问题的观察，导致实践中经验收敛速度很慢.

这种无偏梯度估计只通过选择的问题来更新问题选择算法的参数，而没有包括对可用的但没有选择的问题的观察，导致实践中经验收敛速度很慢。然而，将关于未选择问题的信息合并到梯度计算中可以降低了梯度的方差，稳定了训练过程。接下来，我们使用所有可用的训练问题详细说明对梯度的有偏近似。

近似梯度估计(Approximate Gradient Estimate)
将梯度公式重写：
$${\nabla }_{\varphi }\mathcal{L}\left({\mathbf{\theta }}_i^{\ast }(\gamma ,\varphi ),{\Gamma }_i\right)={\nabla }_{{\theta }_i}\mathcal{L}\left({\mathbf{\theta }}_i^{\ast },{\Gamma }_i\right){\nabla }_{\varphi }{\mathbf{\theta }}_i^{\ast }(\gamma ,\varphi )$$
详细讨论了单时间步长下∇φθ∗i？γ，φ？的计算

$$\begin{array}{rc}{\mathbf{\theta }}_i^{\ast }=\underset{{\theta }_i}{\mathrm{argmin}}{\sum }_{\tau =1}^{t-1}\ell \left(Y_{i,j_i^{(\tau )}},g\left(j_i^{(\tau )};{\mathbf{\theta }}_i\right)\right)+\mathcal{R}\left(\mathbf{\gamma },{\mathbf{\theta }}_i\right)& \\ & +{\sum }_{j\in {\Omega }_i^{(t)}}{w}_j(\varphi )\ell \left(Y_{i,j},g\left(j;{\mathbf{\theta }}_i\right)\right)\end{array}$$

1、初始化全局参数γ，φ、学习率η1、η2、α和内层的梯度下降步数K。
2、随机抽取一小批学生进行训练和元问题集{Ω(1)I，ΓI}I∈B。
1-N
3、根据学生对以前选择的问题的回答，对学生的当前状态(T)进行编码。
4、为每个学生选择问题j(T)i∼Π(x(T)i；φ)。
5、优化θ∗在等式6中，使用学习率α和k GD步骤对观察到的响应{Yi，j（1:t）i}。
6、使用公式估计无偏(或近似)梯度∇φL(θ∗i，Γi)。8(或等式。11)。
7、更新φ：φ←φ−η2 | B | P i∈B∇φL（θ∗i、 Γi）。
…
8、更新γ

计算复杂性：在训练时，我们需要解决完整的BOBCAT双层优化问题，这在大数据集上是计算密集型的。然而，在测试时，当我们需要为每个学生选择下一个问题时，我们只需要将他们过去的回答作为学习问题选择算法Π(·；φ)的输入，就可以得到选择的问题作为输出；

Experiments

详细介绍了我们在五个真实世界的学生反应数据集上进行的定量和定性实验，以验证CAT的有效性。

Datasets：EdNet2、Junyi 3、EEDI-1、EEDI-24和ASSISTments5

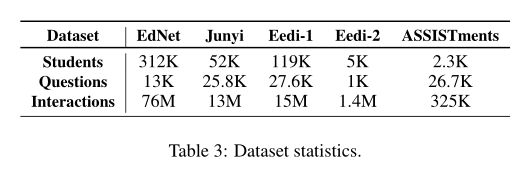
Training：对所有数据集进行5次交叉验证；对于每个折叠，我们分别使用60%-20%-20%的学生进行培训、验证和测试。

Testing ：对于BOBCAT，我们将每个学生回答的问题划分为训练(Ω(1)I，80%)和元(ΓI，20%)问题集。为了防止过度拟合，我们在每个训练时期随机生成这些分区。

Evaluation Metric：使用准确率和接收器操作特征曲线下的面积两个指标来评估所有方法在元集ΓI上预测二进制值学生回答的性能。

方法和基线：
IRT–Active，一种基于不确定性抽样的主动学习问题选择算法，它选择下一个最接近学生当前能力估计的问题作为基线。
IRT-Random，用额外的基线随机选择下一个问题
使用IRT模型(我们称为BiIRT)和神经网络(我们称为BiNN)作为响应模型的情况。

除了上面的-Activeand-Randomum算法外，我们还使用了关于问题选择算法参数φ的-无偏梯度(8)和近似(-近似)梯度(11)的学习算法。

网络和超级参数：我们使用逻辑回归和L2范数正则化来训练IRT模型; IRT-Active，我们使用12范数正则化来计算学生当前的能力估计，以惩罚与平均学生能力参数的偏差;BiNN,使用两层完全连接的网络(256隐藏结点，20% dropout rate)

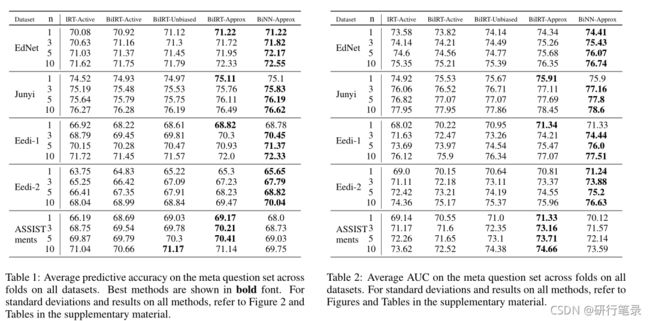
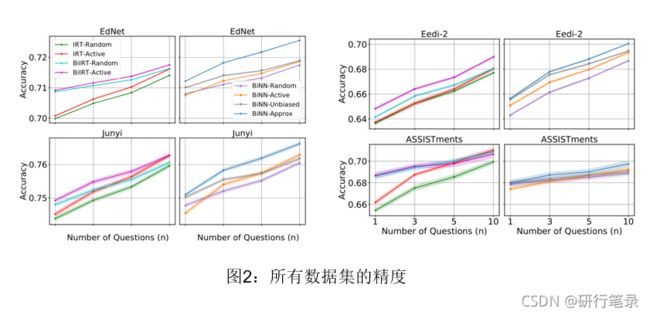
通过上图，可以看出BINN-Approx 效果比较好

还有就是在所有数据集的ACC结果，发现BiIRT还是比较有优势的。

能力评估

传统的是准确估计IRT模型下的学生能力参数，然后利用这些参数进行评分，使用当前能力参数估计ˆθ(N)i和真实能力θi之间的平方误差作为评估度量。
两种比较方法：IRT-Active方法【基于数据训练的底层1PL的IRT模型】和BiIRT-Approx【只使用学习到的模型不可知的问题选择算法进行评估】

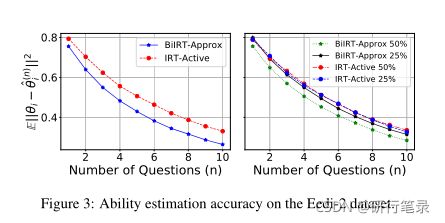
结论：我们看到，尽管BiIRT-Approx的目标不是能力参数估计，但它比IRTActive更有效，并且可以用多达30%的问题达到同样的准确率，显著缩短测试长度。图3(右)显示了在训练数据集的25%和50%上训练的模型的相同比较，随着更多的训练数据可用，BOBCAT可以显著改善。

问题暴露和内容重叠

问题曝光率：就是说同样的题目，对于不同的学生而言，会频繁的暴露给用户。
内容重叠：在CAT中,给学生出的题目与题目之间,相关知识点内容会有重叠.

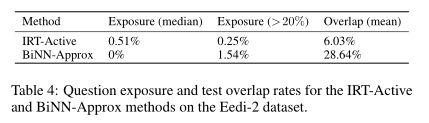
根据上图，可以看出BOBCA T导致的问题曝光率略高于现有的CA T方法，但仍然导致可接受的部分过度曝光的问题。
BOBCAT方法比现有的CAT方法有更高的测试重叠率,这种观察的原因是BOBCA T偏爱一小部分问题，这些问题对学生对其他问题的反应具有很高的预测性，我们接下来将详细解释这些问题。

问题选择

BiIRT/NN-Approx方法偏爱那些高度代表整个问题集的问题，导致表4中有更高的测试重叠率。
MI(计算每个问题与所有其他问题之间的加权互信息)
MI(j,k)代表题目j和k之间的互信息
$$\sum _{x\in \{0,1\}}\sum _{y\in \{0,1\}}\frac{\left|Y_{i,j}=x,Y_{i,,k}=y\right|}{m}\log \frac{m\left|Y_{i,j}=x,Y_{i,k}=y\right|}{\left|Y_{i,,j}=x\Vert Y_{i,,k}=y\right|}$$

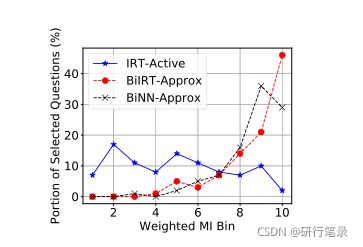
为测试集中的学生绘制了IRT-Active、BiIRT-Approx和Binn-Approx方法从每个库中选择的问题的分数。BiIRT-Approx和Binn-Approx方法倾向于为每个学生提供关于所有其他问题的更多信息的问题。

冲突目标：减少问题暴露和测试重叠率是需要平衡的相互冲突的目标

Conclusions

本文提出了一种面向CAT的双层优化框架BOBCAT，该框架独立于底层的学生响应模型，并从训练数据中学习问题选择算法。通过在五个真实的学生反应数据集上的广泛实验，我们证明了bobcat在缩短测试长度方面可以显著优于现有的CAT方法。

这篇小曾带你将比较重要的部分都已经过了一遍，还有一些细节和实验部分，后期有时间会将实验部分再加以补充。

关注小曾，小曾带你们一起进步！