动手学深度学习笔记（一）

矩阵计算

---

1. 标量导数

一般的标量导数表示切线的斜率

2. 亚导数

将导数拓展到不可微的函数。在函数的不可导点，将导数（斜率）取为一个范围内的任意值。

如，对于函数：
$$y=|x|$$

其导数可以记为：
$$\frac{\partial |x|}{\partial x}=\{\begin{array}{ll}1& ifx>0\\ -1& ifx<0\\ a& ifx=0,a\in [-1,1]\end{array}$$

函数 $\max (x,0)$ 的导数可以记为：
$$\frac{\partial \max (x,0)}{\partial x}=\{\begin{array}{ll}1& ifx>0\\ 0& ifx<0\\ a& ifx=0,a\in [-1,1]\end{array}$$

3. 梯度

导数在向量的拓展。

\quad	标量 $x$	向量 $\mathbf{x}$
标量 $y$	$$\frac{\partial y}{\partial x}（标量）$$	$$\frac{\partial y}{\partial \mathbf{x}}（行向量）$$
向量 $\mathbf{y}$	$$\frac{\partial \mathbf{y}}{\partial x}（列向量）$$	$$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}（矩阵）$$

1. $y$ 是标量，$\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$ 是向量，梯度按照如下方法计算，标量相对于一个列向量的导数是一个行向量（分子布局法），所以下面的计算都要转置。
   $$\frac{\partial y}{\partial \mathbf{x}}=\left[\begin{array}{cccc}\frac{\partial y}{\partial x_1},& \frac{\partial y}{\partial x_2},& \cdots ,& \frac{\partial y}{\partial x_n}\end{array}\right]$$

   如，对于 $y=x_1^2+2x_2^2$，梯度$\frac{\partial y}{\partial \mathbf{x}}=\left[\begin{array}{c}2x_1,4x_2\end{array}\right]$。

   一些梯度的计算：

   y	$sum(\mathbf{x})$	$\Vert x{\Vert }^2$	$⟨\mathbf{u},\mathbf{v}⟩$
   $\frac{\partial y}{\partial \mathbf{x}}$	$$1^T$$	$$2{\mathbf{x}}^T$$	$${\mathbf{u}}^T\frac{\partial \mathbf{v}}{\partial \mathbf{x}}+{\mathbf{v}}^T\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$$

2. $\mathbf{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$ 是矩阵，$x$ 是一个标量，计算梯度的方式如下，得到的是一个列向量（分子布局法）。
   $$\frac{\partial \mathbf{y}}{\partial x}=\left[\begin{array}{c}\frac{\partial y_1}{\partial x}\\ \frac{\partial y_2}{\partial x}\\ ⋮\\ \frac{\partial y_m}{\partial x}\end{array}\right]$$

3. 对于向量 $\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$ 与向量 $\mathbf{y}=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_m\end{array}\right]$，其求梯度的方式如下，最终得到一个矩阵。
   $$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}=\left[\begin{array}{c}\frac{\partial y_1}{\partial \mathbf{x}}\\ \frac{\partial y_2}{\partial \mathbf{x}}\\ ⋮\\ \frac{\partial y_m}{\partial \mathbf{x}}\end{array}\right]=\left[\begin{array}{cccc}\frac{\partial y_1}{\partial x_1},& \frac{\partial y_1}{\partial x_2},& \cdots ,& \frac{\partial y_1}{\partial x_n}\\ \frac{\partial y_2}{\partial x_1},& \frac{\partial y_2}{\partial x_2},& \cdots ,& \frac{\partial y_2}{\partial x_n}\\ & ⋮& & \\ \frac{\partial y_m}{\partial x_1},& \frac{\partial y_m}{\partial x_2},& \cdots ,& \frac{\partial y_m}{\partial x_n}\end{array}\right]$$

$\mathbf{y}$	$\mathbf{x}$	$\mathbf{A}\mathbf{x}$	$${\mathbf{x}}^T\mathbf{A}$$	$$a\mathbf{u}$$	$$\mathbf{A}\mathbf{u}$$
$\frac{\partial \mathbf{y}}{\partial \mathbf{x}}$	$$\mathbf{I}$$	$$\mathbf{A}$$	$${\mathbf{A}}^T$$	$$a\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$$	$$\mathbf{A}\frac{\partial \mathbf{u}}{\partial \mathbf{x}}$$

• $a$，$\mathbf{a}$ 和 $\mathbf{A}$ 中都不包含 $\mathbf{x}$

相关链接：

1. 矩阵求导的本质与分子布局、分母布局的本质（矩阵求导——本质篇）
2. 矩阵求导公式的数学推导（矩阵求导——基础篇）
3. 矩阵求导公式的数学推导（矩阵求导——进阶篇）

4. 向量链式法则

• 标量的链式法则：

  若 $y=f(u),u=g(x)$，则 $y$ 相对于 $x$ 的导数可以表示为：
  $$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u}\frac{\partial u}{\partial x}$$

• 向量的链式求导法则：

  类型	求导
  $y$ 是标量，$u$ 是标量，$\mathbf{x}$ 是向量	$\underset{(1,n)}{\frac{\partial y}{\partial \mathbf{x}}}=\underset{(1,)}{\frac{\partial y}{\partial u}}\underset{(1,n)}{\frac{\partial u}{\partial \mathbf{x}}}$
  $y$ 是标量，$\mathbf{u}$ 是向量，$\mathbf{x}$ 是向量	$\underset{(1,n)}{\frac{\partial y}{\partial \mathbf{x}}}=\underset{(1,k)}{\frac{\partial y}{\partial \mathbf{u}}}\underset{(k,n)}{\frac{\partial \mathbf{u}}{\partial \mathbf{x}}}$
  $\mathbf{y}$ 是向量，$\mathbf{u}$ 是向量，$\mathbf{x}$ 是向量	$\underset{(m,n)}{\frac{\partial \mathbf{y}}{\partial \mathbf{x}}}=\underset{(1,k)}{\frac{\partial \mathbf{y}}{\partial \mathbf{u}}}\underset{(k,n)}{\frac{\partial \mathbf{u}}{\partial \mathbf{x}}}$

例子：

• 对于一个表达式 $z=(⟨\mathbf{x},\mathbf{w}⟩-y{)}^2$，其中 $\mathbf{x},\mathbf{w}\in {\mathbb{R}}^n,y\in \mathbb{R}$，计算 $\frac{\partial z}{\partial \mathbf{w}}$ 的过程如下：

  1. 首先将其中的变量求导，记 $a=⟨\mathbf{x},\mathbf{w}⟩,b=a-y,z=b^2$

  2. 使用链式求导对每个中间变量求导
     $$\begin{array}{rl}\frac{\partial z}{\partial \mathbf{w}}& =\frac{\partial z}{\partial b}\frac{\partial b}{\partial a}\frac{\partial a}{\partial \mathbf{w}}\\ & =\frac{\partial b^2}{\partial b}\frac{\partial (a-y)}{\partial a}\frac{\partial ⟨\mathbf{x},\mathbf{w}⟩}{\partial \mathbf{w}}\\ & =2b\cdot 1\cdot {\mathbf{x}}^T\\ & =2(⟨\mathbf{x},\mathbf{w}⟩-y){\mathbf{x}}^T\end{array}$$

5. 自动求导

自动求导是计算一个函数在指定值上的导数，即对于一个 $y=f(x)$ 的表达式，对于某一个 $x=c$，$f^{\prime }(c)$ 的值是什么。

自动求导是根据计算图进行详细计算的，也就是给定一个表达式：

1. 首先将该表达式分解成一个一个的操作子
2. 使用操作子就可以将整个表达式表示为一个无环图

如，对于上面例子的表达式，$z=(⟨\mathbf{x},\mathbf{w}⟩-y{)}^2$，$a,b,z$ 就算单个的计算子，它们可以构成如下的计算图，其中每个圈表示一个表达式或输入。

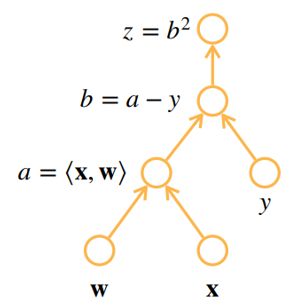
构造出计算图后，根据链式求导法则：
$$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}}\cdots \frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}$$

可以通过如下两种方式实现自动求导：

1. 正向累积。先计算 $\frac{\partial u_1}{\partial x}$ ，再计算 $\frac{\partial u_2}{\partial u_1}$，之后依次向前计算
   $$\frac{\partial y}{\partial x}=\frac{\partial y}{\partial u_n}\left(\frac{\partial u_n}{\partial u_{n-1}}\left(\cdots \left(\frac{\partial u_2}{\partial u_1}\frac{\partial u_1}{\partial x}\right)\right)\right)$$

   正向累计可以根据计算图，从下向上依次计算每个结点相对于下一个参数的导数。

2. 反向累积（反向传播）。先计算 $\frac{\partial y}{\partial u_n}$ ，再计算 $\frac{\partial u_n}{\partial u_{n-1}}$，之后依次向后计算。
   $$\frac{\partial y}{\partial x}=\left(\left(\left(\frac{\partial y}{\partial u_n}\frac{\partial u_n}{\partial u_{n-1}}\right)\cdots \right)\frac{\partial u_2}{\partial u_1}\right)\frac{\partial u_1}{\partial x}$$

   反向累积需要根据计算图从上向下依次求导，求导过程中需要将正向计算中的结果拿来构成每个结点的求导结果并保存为中间结果。如下所示：
   

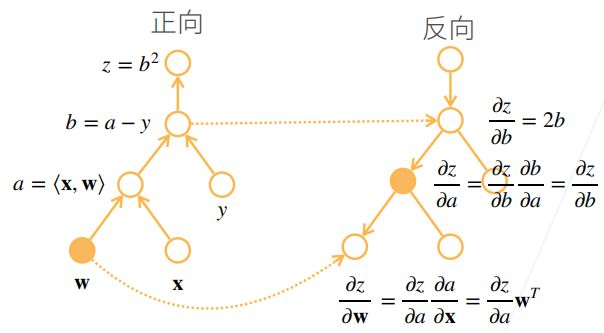
• 反向累积中，计算复杂度为 $O(n)$，内存复杂度为 $O(n)$，因为要存储正向的所有中间结果，所以更加耗费资源。
• 正向累积中，计算一个变量的时间复杂度为 $O(n)$（即从下向上扫一遍），对于多个变量的计算会使计算复杂度非常大。内存复杂度为 $O(1)$，不需要保存中间的结果。

6. PyTorch 自动求导

• 若要计算 $y=2{\mathbf{x}}^T\mathbf{x}$ 关于行向量 $\mathbf{x}$ 的导数，可以通过如下步骤。

  1. 构造 $\mathbf{x}$ 向量，并指定在 x.grad 中保存计算出来的梯度

     # 1. 先创建 x ，再指定 x 可以求导
     >>> x = torch.arange(4.0)
     >>> x
     tensor([0., 1., 2., 3.])
     >>> x.requires_grad_(True)
     tensor([0., 1., 2., 3.], requires_grad=True)
     >>> x.grad     #默认为 None
     
     # 2. 在创建 x 同时指定 x 可以求导
     >>> x = torch.arange(4.0, requires_grad=True)
     >>> x
     tensor([0., 1., 2., 3.], requires_grad=True)
     >>> x.grad     #默认为 None
     

  2. 利用 $\mathbf{x}$ 计算 $y$

     >>> y = 2 * torch.dot(x,x)           #计算内积
     >>> y
     tensor(28., grad_fn=<MulBackward0>)  #grad_fn 保存 y 的运算信息，表明 y 是由 x 构建的
     >>> y.grad_fn
     <MulBackward0 object at 0x00000211287EEFD0>
     

  3. 调用反向传播函数 y.backward() 自动计算 $y$ 关于 $\mathbf{x}$ 每个分量的梯度

     >>> y.backward()
     >>> x.grad
     tensor([ 0.,  4.,  8., 12.])
     
     >>> x.grad == 4 * x
     tensor([True, True, True, True])
     

  其计算的本质就是构造出 $y=f(x)$ 的表达式，上式为 $y=2(x_1^2+x_2^2+x_3^2+x_4^2)$ ，之后将向量 $\mathbf{x}$ 中的每个值都带入计算，得到 $\mathbf{x}=\left[\begin{array}{c}{x}_1,x_2,\cdots ,x_n\end{array}\right]$ 中每个位置的变量对应的求导公式 $y^{\prime }=f^{\prime }(\mathbf{x})=\left[\begin{array}{c}{f}^{\prime }(x_1),f^{\prime }(x_2),\cdots ,f^{\prime }(x_n)\end{array}\right]=\left[\begin{array}{c}4x_1^2,4x_2^2,4x_3^2,4x_4^2\end{array}\right]$，再将值带入对应位置。

• 下面展示了计算 $x$ 的累加和的梯度

  在默认情况下，PyTorch 会 累加梯度，使用 x.grad.zero_() 可以清除之前的值

  >>> x.grad.zero_()
  tensor([0., 0., 0., 0.])
  >>> x.grad
  tensor([0., 0., 0., 0.])
  
  >>> y = x.sum()
  >>> y.backward()
  >>> x.grad
  tensor([1., 1., 1., 1.])
  

• 使用 y.backward() 计算梯度时必须保证 y 是一个标量，在数学上是不允许对非标量求导的，如下所示，一般情况下我们首先对 y 求和，求和之后是一个标量，再进行求导。

  >>> x.grad.zero_()
  >>> y = x *x
  >>> y.backward()
  Traceback (most recent call last):
    File "", line 1, in <module>
    File "D:\Applications\Anaconda\lib\site-packages\torch\tensor.py", line 221, in backward
      torch.autograd.backward(self, gradient, retain_graph, create_graph)
    File "D:\Applications\Anaconda\lib\site-packages\torch\autograd\__init__.py", line 126, in backward
      grad_tensors_ = _make_grads(tensors, grad_tensors_)
    File "D:\Applications\Anaconda\lib\site-packages\torch\autograd\__init__.py", line 50, in _make_grads
      raise RuntimeError("grad can be implicitly created only for scalar outputs")
  RuntimeError: grad can be implicitly created only for scalar outputs
  
  >>> y.sum().backward()
  >>> x.grad
  tensor([0., 2., 4., 6.])
  

• 将某些计算移动到记录的计算图之外，即通过 y.detach() 命令使得中间变量 $y$ 成为一个常数，对于包含 $y$ 的表达式，当计算梯度时候会将 $y$ 视为常数

  #1. 对 y 执行 detach()
  >>> x.grad.zero_()
  tensor([0., 0., 0., 0.])
  >>> y = x * x
  >>> u = y.detach()
  >>> z = u * x
  >>> z.sum().backward()
  
  >>> x.grad == u
  tensor([True, True, True, True])
  >>> x.grad
  tensor([0., 1., 4., 9.])
  
  #2. 不对 y 执行 detach()
  >>> x.grad.zero_()
  tensor([0., 0., 0., 0.])
  >>> y = x * x
  >>> z = y * x
  >>> z.sum().backward()
  >>> x.grad
  tensor([ 0.,  3., 12., 27.])
  
  #3. 因为 y 是 x 的函数，所以直接对 y 进行梯度求解没有影响，但是不能对 u 求导
  >>> x.grad.zero_()
  tensor([0., 0., 0., 0.])
  >>> y.sum().backward()
  >>> x.grad
  tensor([0., 2., 4., 6.])
  
  >>> u.sum().backward()
  RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn