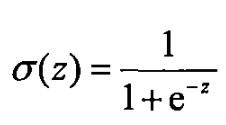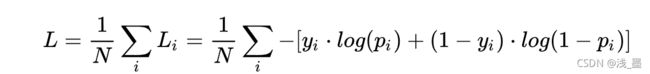多个逻辑回归二分类器实现minist手写数字识别(Python 仅使用numpy实现)
多分类问题可以转换为多个二分类问题,例如,需要完成对手写数字的十分类时,可以采用依次对每个数字(0-9)进行二分类的方式,最终对每次分类中计算出的正样本概率值进行排序,选择概率最高的数字作为分类的结果。
整个过程需要训练10个分类模型(0-9这十个数字每个数字训练一个分类模型),若模型的输入为数字x,则分别使用这10个模型对x进行分类,对每次分类的逻辑回归输出值(即正样本的概率)进行排序,取最大的值所对应的标签作为最终的分类结果。
首先,采用Sigmoid函数作为逻辑回归的激活函数:
代码实现如下:
def logistic(X):
if(X>=0):
return 1.0 / (1.0 + np.exp(-X))
else:
return np.exp(X)/(1.0 + np.exp(X))采用交叉熵作为损失函数,在二分类下,交叉熵损失函数如下:
代码实现如下:
def cross_entropy(Y, P):
Y = np.float_(Y)
P = np.float_(P)
return -np.sum(Y * np.log(P + 1e-10) + (1 - Y) * np.log(1 - P + 1e-10))L对权重w的偏导数为:(logistic - y)* x , 其中logistic为前向传播经过Sigmoid函数激活后的值,其范围在0到1之间。
L对偏置b的偏导数为:(logistic - y)
故在反向传播中,参数w和b的更新如下:
def backward(w,b,data,y,logistic,l_rate):
for i in range(len(w)):
w[i] -= l_rate * (logistic - y)*data[i]
b -= l_rate * (logistic - y)
return (w,b)其中l_rate为学习率
模型的训练过程如下(每个训练样本更新一次权重,每个epoch执行一次评估):
def train(epoch,l_rate,num):
training_data, validation_data, test_data = get_binary_classification_data(num)
w,b = init_weight()
print("Start train num",num,"...")
for i in range(epoch):
print("epoch",i+1)
loss = 0.0
for i in range(len(training_data)):
logistic = forward(training_data[i][0],w,b)
w, b = backward(w, b, training_data[i][0], training_data[i][1], logistic, l_rate)
loss += cross_entropy(training_data[i][1],logistic)
loss = loss/len(training_data)
print("loss = ", loss)
#验证
count = 0
for item in validation_data:
logistic = forward(item[0], w, b)
pre = 0
if(logistic>=0.5):
pre = 1
if(pre == item[1]):
count += 1
print("The accuracy rate is:",count/len(validation_data))
f = open("../logistic_model/"+str(num)+".json","w")
data = {"weights": w,
"biases": b}
json.dump(data, f)其中num表示当前针对数字num训练二分类模型,其范围为0-9
如图所示,使用上述方法分别对每个num训练出一个模型
接下来,对于输入的数字,使用上图保存的十个模型对其进行分类,对Sigmoid函数的输出值进行排序,最终输出最大值对应的标签即可:
def multi_classification():
print("Loading data...")
training_data, validation_data, test_data = load_data_wrapper()
print("Loading para...")
para = load_para()
count = 0
print("Start test...")
for item in test_data:
pre = -1
max = 0
for i in range(10):
logistic = forward(item[0].reshape(1,784)[0], para[i][0], para[i][1])
if logistic > max:
max = logistic
pre = i
if(pre == item[1]):
count += 1
print("The accuracy rate is: ",count/len(test_data))
load_para()函数的作用是加载模型文件,其实现如下:
def load_para():
para = []
for i in range(0,10):
f = open("../logistic_model/"+str(i)+".json","r")
data = json.load(f)
f.close()
weights = data["weights"]
biases = data["biases"]
para.append([weights,biases])
return para这样,一个基于逻辑回归二分类分类器的手写数字识别算法就完成啦!
最后贴上完整的代码:
'''
逻辑回归函数
'''
def logistic(X):
if(X>=0):
return 1.0 / (1.0 + np.exp(-X))
else:
return np.exp(X)/(1.0 + np.exp(X))
'''
交叉熵损失函数
'''
def cross_entropy(Y, P):
Y = np.float_(Y)
P = np.float_(P)
return -np.sum(Y * np.log(P + 1e-10) + (1 - Y) * np.log(1 - P + 1e-10))
"""
加载数据
"""
def load_data():
f = gzip.open('../data/mnist.pkl.gz', 'rb')
training_data, validation_data, test_data = pickle.load(f,encoding='bytes')
f.close()
return (training_data, validation_data, test_data)
"""
将数据格式化
"""
def load_data_wrapper():
tr_d, va_d, te_d = load_data()
training_inputs = [np.reshape(x, (784, 1)) for x in tr_d[0]]
training_data = list(zip(training_inputs, tr_d[1]))
validation_inputs = [np.reshape(x, (784, 1)) for x in va_d[0]]
validation_data = list(zip(validation_inputs, va_d[1]))
test_inputs = [np.reshape(x, (784, 1)) for x in te_d[0]]
test_data = list(zip(test_inputs, te_d[1]))
return (training_data, validation_data, test_data)
'''
将原始数据集标签转为二分类
'''
def get_binary_classification_data(num):
training_data, validation_data, test_data = load_data_wrapper()
bin_training_data = []
bin_validation_data = []
bin_test_data = []
for item in training_data:
temp = []
temp.append(item[0].reshape(1,784)[0])
if(item[1] == num):
temp.append(1)
else:
temp.append(0)
bin_training_data.append(temp)
for item in validation_data:
temp = []
temp.append(item[0].reshape(1,784)[0])
if (item[1] == num):
temp.append(1)
else:
temp.append(0)
bin_validation_data.append(temp)
for item in test_data:
temp = []
temp.append(item[0].reshape(1,784)[0])
if (item[1] == num):
temp.append(1)
else:
temp.append(0)
bin_test_data.append(temp)
return (bin_training_data, bin_validation_data, bin_test_data)
'''
初始化权重
'''
def init_weight():
w = []
for i in range(784):
w.append(random.random())
b = random.random()
return (w,b)
'''
前向传播
'''
def forward(data,w,b):
temp = 0
temp += np.dot(data,w)
temp += b
return logistic(temp)
'''
反向传播
'''
def backward(w,b,data,y,logistic,l_rate):
for i in range(len(w)):
w[i] -= l_rate * (logistic - y)*data[i]
b -= l_rate * (logistic - y)
return (w,b)
"""
训练二分类模型
"""
def train(epoch,l_rate,num):
training_data, validation_data, test_data = get_binary_classification_data(num)
w,b = init_weight()
print("Start train num",num,"...")
for i in range(epoch):
print("epoch",i+1)
loss = 0.0
for i in range(len(training_data)):
logistic = forward(training_data[i][0],w,b)
w, b = backward(w, b, training_data[i][0], training_data[i][1], logistic, l_rate)
loss += cross_entropy(training_data[i][1],logistic)
loss = loss/len(training_data)
print("loss = ", loss)
#验证
count = 0
for item in validation_data:
logistic = forward(item[0], w, b)
pre = 0
if(logistic>=0.5):
pre = 1
if(pre == item[1]):
count += 1
print("The accuracy rate is:",count/len(validation_data))
f = open("../logistic_model/"+str(num)+".json","w")
data = {"weights": w,
"biases": b}
json.dump(data, f)
"""
从保存的模型中加载参数
"""
def load_para():
para = []
for i in range(0,10):
f = open("../logistic_model/"+str(i)+".json","r")
data = json.load(f)
f.close()
weights = data["weights"]
biases = data["biases"]
para.append([weights,biases])
return para
"""
利用二分类模型构建多分类分类器
"""
def multi_classification():
print("Loading data...")
training_data, validation_data, test_data = load_data_wrapper()
print("Loading para...")
para = load_para()
count = 0
print("Start test...")
for item in test_data:
pre = -1
max = 0
for i in range(10):
logistic = forward(item[0].reshape(1,784)[0], para[i][0], para[i][1])
if logistic > max:
max = logistic
pre = i
if(pre == item[1]):
count += 1
print("The accuracy rate is: ",count/len(test_data))
if __name__ == '__main__':
train(10,0.1,1)
#load_para()
#multi_classification()