C++实现疫情感染扩散模型

题目如下：  

我们对疫情的感染过程进行以下数学建模：

1. 将人简化为质点；
2. 人在活动区域内随机行走，行走规则为：每个人只能向上、下、左、右四个方向行走，向四个方向行走的概率相等，行走速度V为1米/时间步，在活动区域边界处，向离开活动区域方向行走的概率降为0，向其他三个方向行走的概率不变；
3. 感染半径R为2米；
4. 未接种疫苗时，感染概率P（只要在感染半径内）为0.6；
5. 感染时间T为10个时间步；
6. 致死概率D（被感染者在感染时间内每个时间步都有可能致死）为0.001，致死后移除出活动区域；
7. 非致死，即治愈，被治愈者不再被感染；

活动区域为200米*200米的正方形，被划分为1米*1米的网格点。初始化时，每个人随机出现在活动区域内的网格点上，并且所有人除致死外均不离开活动区域，随机选择一个人，其初始状态为被感染（即零号感染者）。

请模拟出上述传播过程。

题解：

首先，定义Person类：

class Person
{	
	public:
		//公共参数
		int activeRadius = 200; //活动区域
		int V = 1; //行走速度
		int R = 2; //感染半径
		double P = 0.6; //感染概率
		int T = 10; //感染时间
		double D = 0.001; //致死概率

		//个人参数
		int positionX; //X方向位置
		int positionY; //Y方向位置
		bool isInfected = false; //是否被感染
		bool isDead = false; //是否死亡
		bool isCured = false;
		int infectedTimeRemain; //当前剩余感染时间


		//成员函数
		Person(int infected); //构造函数
		void Move(); //移动
		vector JudgeState(int X, int Y); //判断当前移动状态
		void Infected(); //执行感染操作
		void Dead(); //执行死亡操作
		void getString();
};

首先，使用随机数初始化当前Person的位置，并在所有人中随机初始化一个感染者：

Person::Person(int infected)
{
	//初始化位置
	positionX = rand() % (activeRadius + 1);
	positionY = rand() % (activeRadius + 1);
	//初始化感染状态
	isInfected = infected == 0 ? false:true;
}

第二步，模拟Person的移动，在移动前，首先需要根据其位置坐标判断其可以执行的移动方式，这里使用了枚举的方式，将当前状态下可以执行的移动方式保存下来：

vector Person::JudgeState(int X, int Y)
{
	//1为向左,2为向上,3为向右,4为向下
	vector ans;

	if (X == 0)
	{
		if (Y == 0)
		{
			ans.push_back(2);
			ans.push_back(3);
			return ans;
		}
		else if (Y == activeRadius)
		{
			ans.push_back(3);
			ans.push_back(4);
			return ans;
		}
		else
		{
			ans.push_back(2);
			ans.push_back(3);
			ans.push_back(4);
			return ans;
		}
	}
	else if (X == activeRadius)
	{
		if (Y == 0)
		{
			ans.push_back(1);
			ans.push_back(2);
			return ans;
		}
		else if (Y == activeRadius)
		{
			ans.push_back(1);
			ans.push_back(4);
			return ans;
		}
		else
		{
			ans.push_back(1);
			ans.push_back(2);
			ans.push_back(4);
			return ans;
		}
	}
	else
	{
		if (Y == 0)
		{
			ans.push_back(1);
			ans.push_back(2);
			ans.push_back(3);
			return ans;
		}
		else if (Y == activeRadius)
		{
			ans.push_back(1);
			ans.push_back(3);
			ans.push_back(4);
			return ans;
		}
		else
		{
			ans.push_back(1);
			ans.push_back(2);
			ans.push_back(3);
			ans.push_back(4);
			return ans;
		}
	}
}

接下来，定义移动操作，这里采用了随机的方式，首先获取当前状态下可以进行的移动方式数组，随机从该数组中获取一个移动操作：

void Person::Move()
{
	vector state = JudgeState(positionX, positionY);
	//初始化随机种子
	int r = rand() % state.size();
	int direction = state[r];
	//1为向左,2为向上,3为向右,4为向下
	if (direction == 1)
	{
		positionX -= 1;
	}
	if (direction == 2)
	{
		positionY += 1;
	}
	if (direction == 3)
	{
		positionX += 1;
	}
	if (direction == 4)
	{
		positionY -= 1;
	}
}

感染操作定义如下（P为感染概率）这里使用rand()生成一个整数，并取其最后一位，+1使得其范围变为[1,10]，若此时得到的数字≤ P*10，则处于概率范围内，故被感染：

void Person::Infected()
{
	int r = rand() % 10 + 1;
	if (r <= P * 10)
	{
		isInfected = true;
		infectedTimeRemain = T;
	}
}

死亡操作定义如下（概率为1/1000）：

void Person::Dead()
{
	int r = rand() % 1000 + 1;
	if (r == 1)
	{
		//执行死亡
		isDead = true;
	}
}

到这里，Person类就实现完了，接下来是主函数的实现：

首先是一个工具函数，用于计算两点之间的欧氏距离：

double Distance(int x1, int y1, int x2, int y2)
{
	int ans = sqrt(pow(x2 - x1, 2) + pow(y2 - y1, 2));
	return ans;
}

主函数中包含了题目中所提到的人物移动及感染过程，其实现如下：

int main()
{
	//活动人数
	int personNum = 10000;
	//时间步
	int timeStep = 20;
   //初始化所有Person
	cout << "initializing......\n";
	vector personList;
	//随机选择一个人物作为零号感染者
	srand(time(0));
	int r = rand() % personNum;
	srand(time(0));
	for (int i = 0; i < personNum; i++)
	{
		int infected = 0;
		if (i == r) 
		{
			infected = 1;
		}
		Person* p = new Person(infected);
		personList.push_back(p);
	}

	cout << "moving......\n";
	//移动,当前迭代timeStep个时间步
	for (int i = 0; i < timeStep; i++)
	{
		for (Person* p : personList) 
		{
			//若当前人物已死,则不再参与
			if (p->isDead) { continue; }
			//如果当前已经感染
			if (p->isInfected)
			{
				//若当前剩余感染时间为0,则已治愈
				if (p->infectedTimeRemain == 0)
				{
					p->isInfected = false;
					p->isCured = true;
				}
				else 
				{
					//否则,当前感染时间-1,并尝试死亡操作
					p->infectedTimeRemain -= 1;
					p->Dead();
				}
			}
			//如果当前未感染
			else 
			{
				//若当前已治愈,则不会再感染
				if (p->isCured) { continue; }
			    //判断当前感染半径内是否存在感染者
				for (Person* temp : personList) 
				{
					//如果感染半径内存在感染者,则尝试感染操作
					if (temp->isInfected ==  true && Distance(p->positionX, p->positionY, temp->positionX, temp->positionY) <= p->R)
					{
						//尝试感染操作
						p->Infected();
					}
				}
			}
			//移动
			p->Move();
		}
		int infected = 0;
		int dead = 0;
		int cure = 0;
		for (Person* p : personList)
		{
			if (p->isDead)
			{
				dead += 1;
				continue;
			}
			if (p->isInfected)
			{
				infected += 1;
				continue;
			}
			if (p->isCured)
			{
				cure += 1;
			}
		}
		cout << "第" << i + 1<< "轮:";
		cout << "死亡:" << dead << "人   ";
		cout << "目前仍感染:" << infected << "人   ";
		cout << "治愈:" << cure << "人\n";
	}
	for (Person* p : personList) 
	{
		delete(p);
	}
	
}

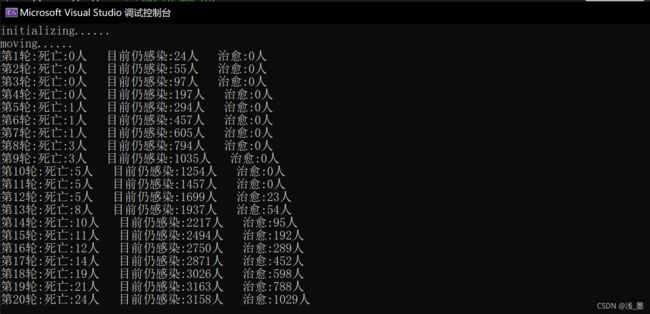
最后，当人数为10000，执行20个时间步时，执行结果如下：