雷达测角算法（二）---单脉冲和差波束测角

对于数字相控阵而言，其对目标角度的测量能力是评估性能的重要指标之一。常用的测角方向有单脉冲比幅法，单脉冲比相法等。鉴于单脉冲和差波束测角具有易于实现且精度高的特性，因此在工程中常被相控阵用于波达角估计。

目录

数字波束形成(DBF)

和差波束测角原理

---

数字波束形成(DBF)

        在讲解单脉冲和差波束测角原理前，需要一定对数字波束形成有一定的了解。相控阵天线是由多个天线单元按某种规律排列而成的天线单元网络，而数字波束形成是相控阵领域特有的技术。

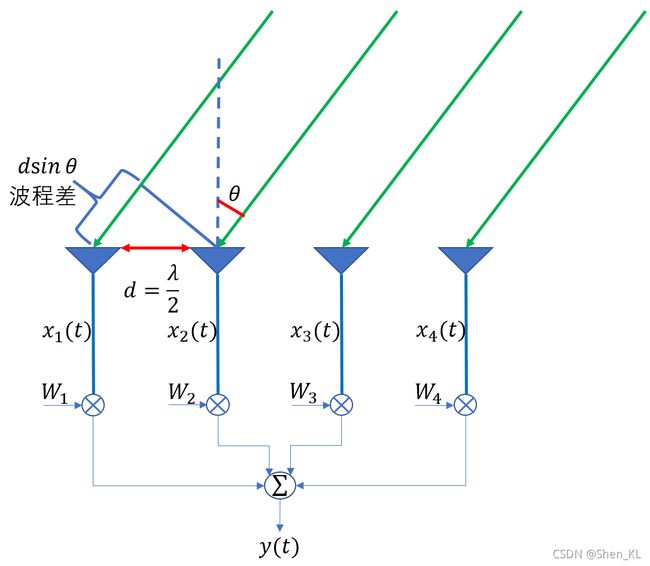
        对于无方向性的单个天线单元而言，其方向图是全向的。但是，我们可以利用数字信号处理的方式，对每一个天线阵元通道做相位补偿（此处补偿的相位差是由天线阵元空间位置的差异导致每个阵元接收信号的波程差引起的），使得天线阵元对期望方向的信号做同相叠加，最大化该方向的接受增益，实现该方向的是波束形成。而相位补偿最常用的方式就是加权。如下图所示，

        那么，现在问题便是权系数的选择。假设有一个由N个阵元组成的线阵，有一来自方向的来波信号入射到阵元上，其导向矢量可以写为

        其中，为阵元间距，为波长。则入射信号可以写为,为加性噪声。对入射信号进行加权后，可以表示为,为加权权矢量，。

        若想实现对方向的波束形成，则令即可。现在假设一仿真背景，有一个由11个阵元构成的均匀线阵(ULA),阵元间距为半波长，实现对方向15°的波束形成。以下为仿真代码与结果图，

%%天线方向图
clear all;clc;close all;
N=11;%阵元数目
d_lambda=0.5;%阵元间距比波长
theta0=15;%波束指向
theta=-90:0.1:90;
win=taylorwin(N);
theta0=theta0*pi/180;
theta=theta*pi/180;
a0=exp(j*2*pi*d_lambda*(0:N-1)'*sin(theta0));%导向矢量
a=exp(j*2*pi*d_lambda*(0:N-1)'*sin(theta));
ww=a0.*win;//对权矢量加窗
pattern=abs(ww'*a);
pattern1=abs(a0'*a);
figure;
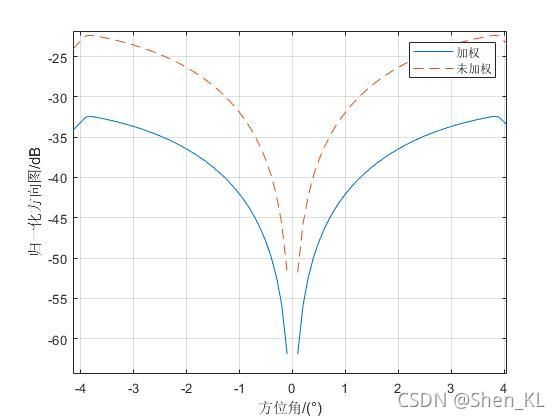
plot(theta*180/pi,20*log10(pattern/max(pattern)),'-',theta*180/pi,20*log10(pattern1/max(pattern1)),'--');
xlabel('方位角/(°)');ylabel('归一化方向图/dB');
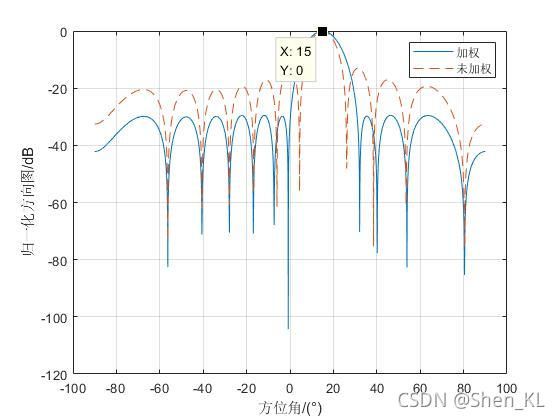
legend('加权','未加权');
grid on;

        由仿真结果图不难发现，加权矢量后，实现了对15°方向的最大接受增益，而抑制了其他方向的信号，同时当加权矢量进行加窗处理后，可有效抑制副瓣电平。同时相信有的读者已经发现，波束形成的方式与我们平时设计滤波器的过程十分相似。其实，波束形成就是一种“滤波”，只不过我们之前接触的都是时域中的滤波器，其滤波器表现形式为幅频响应，而波束形成为空域滤波，其表现形式为方向图。本质上都是滤除不关心的信号分量，得到期望信号。

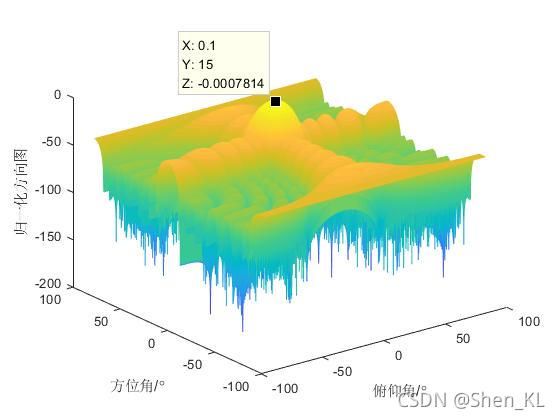
        同样，波束形成可以由线阵拓展到面阵，实现对二维信号的滤波，下图为对方向角0°，俯仰角15°方向的波束形成天线方向图。

        

和差波束测角原理

        了解何为波束形成后，再来了解波束和差原理就变得相对简单些。

        波束和差原理简单来说就是对波束形成方向形成主瓣(目标方向需要在主瓣内)，即和波束；同时在波束形成方向形成零陷，即差波束。通过和差波束比值得到某一确定的值，从而知道目标方向偏离波束中心的方向大小，最后确定目标位置。

        和波束便是运用到上文所提及的波束形成原理。现在讲解差波束的形成原理。差波束有两种形成方式。第一种方法，假设和波束指向，则在,两个方向分别形成波束，并相减，即可到到差波束，如下图所示。

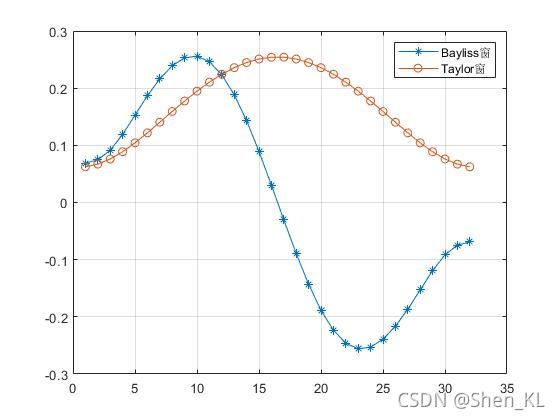
         第二种方法便是需要Bayliss窗函数。Bayliss分布是一种典型的差分布，可以使得阵列左右单元的相位互相反相。由下图窗函数值可以很直观的看出为何Bayliss窗函数可以实现相位的反相。

         现在简要介绍一下Bayliss窗函数系数的求解方法(警告！前方一大堆公式来袭)，其权系数表达式为

        其中，为等副瓣电平个数，为天线个数，表达式为

            其中，为副瓣电平，一般取{15，20，25，30，35，40}dB。下表是的系数表格

多项式系数表格

多项式系数
	0.30387530	-0.05042922	-0.00027989	-0.00000343	-0.0000002
	0.98583020	-0.03338850	0.00014064	0.00000190	0.0000001
	2.00337487	-0.01141548	0.00041590	0.00000373	0.0000001
	3.00636321	-0.00683394	0.00029281	0.00000161	0.0000000
	4.00518423	-0.00501795	0.00021735	0.00000088	0.0000000

        上述公式看似复杂，其实借助MATLAB可以很轻松的求出Bayliss窗函数的系数

        下面利用上述公式做出差波束的方向图，副瓣比取30dB，波束指向0°，等副瓣电平个数取8，天线个数32，阵元间距半波长。代码中已经提前算出Bayliss的五个系数，感兴趣的读者可以自己在验算一下，

clear all;clc;close all;
N=32;%阵元数目
d_lambda=0.5;%阵元间距波长比 取d=lambda/2
theta0=0;%波束指向
theta=-90:0.1:90;
win=taylorwin(N);%泰勒窗
win=win/norm(win);
theta0=theta0*pi/180;
theta=theta*pi/180;
a0=exp(1i*2*pi*d_lambda*(0:N-1)'*sin(theta0));%导向矢量
a=exp(1i*2*pi*d_lambda*(0:N-1)'*sin(theta));

n_=8;%等副瓣电平个数
Omega1=zeros(n_,1);
SLR=-30;%副瓣电平 dB单位
 switch SLR       
     case -15
         A=0.9988; 
         Omega=[1.5170,2.2607,3.1693,4.1264]; 
     case -20
         A=1.1959; 
         Omega=[1.7107,2.3842,3.2473,4.1854]; 
     case -25
         A=1.3651; 
         Omega=[1.9178,2.5295,3.3351,4.2527]; 
     case -30 
         A=1.6413; 
         Omega=[2.1438,2.7004,3.4314,4.3276]; 
     case -35
         A=1.5730; 
         Omega=[2.3953,2.9025,3.5352,4.4093]; 
     case -40
         A=1.5807; 
         Omega=[2.6808,3.1427,3.6452,4.4973];       
  end

 Omega1(1:4)=Omega;
 for i=5:n_
    Omega1(i)=sqrt(A^2+i^2);
 end
 B=ones(1,n_);
 SIGMA=(n_+0.5)/(sqrt(A^2+n_^2));
 TEMP1=ones(1,n_);
 TEMP2=ones(1,n_);
 for i=1:n_
    for j=1:n_-1
        TEMP1(i)=TEMP1(i)*(1-(i-1+0.5)^2/(Omega1(j)*SIGMA)^2);
    end
 end
  for i=1:n_
    for j=1:n_
        if j~=i
            TEMP2(i)=TEMP2(i)*(1-(i-1+0.5)^2/(j-1+0.5)^2);
        end
    end
 end
 for i=1:n_
     B(i)=1/(2*1i)*(i-1+0.5)^2*(-1)^(i-1)*TEMP1(i)/TEMP2(i);
 end
 w=zeros(N,1);
 for i=1:N
     for j=1:n_
        w(i)=w(i)+B(j)*sin(pi*((j-1)+0.5)*(2*i-N-1)/(N-1));%Bayliss窗函数权值
     end
 end
w=w/norm(w);
ww=a0.*w;
Fd=(ww'*a);
ww=a0.*win;
Fs=(ww'*a);
plot(theta*180/pi,20*log10(abs(Fd)/max(abs(Fs))),'-');
hold on;
plot(theta*180/pi,20*log10(abs(Fs)/max(abs(Fs))),'--');
grid on;legend('差波束','和波束');xlabel('方位角/(°)');ylabel('方向图/dB');
axis([-90 90 -50 0]);
figure;
plot(theta*180/pi,real(Fd./Fs));xlim([-1 1]);xlabel('相对波束中心的方位/(°)');ylabel('归一化方位误差信号');grid on;

         分别将Taylor窗函数矢量、Bayliss窗函数矢量加权到接收信号，得到和波束、差波束信号,,提取归一化方位误差信号

 假设误差信号的多项式拟合系数为(此处取三阶拟合)，则

由波束指向推出目标方位为