Python科学计算:用NumPy快速处理数据
![]()
戳我 -> 卧槽!当当网图书全场4折了!
作者:AI悦创
来源:AI悦创
我来分享一下数据分析中 Numpy 库的使用,本文内容较多,不可能每段代码的输出过程、输出结果分析这显然工作量不是一点点。但我都结合了大量的代码块,希望小伙伴动手运行代码并分析所得到的结果。当你能做到这点的时候,在未来:不管是 Numpy 版本升级导致 API 变化还是其他,你都可以游刃有余的去解决和学习新知识。
而对于结果,分析得不到的结果中规律的小伙伴呢,也不要慌。如果你对本文中的示例代码的运行结果不理解或者其他问题,都可以在博客原文下方留言「点击阅读原文即可」。当然,也可以通过关注公众号:AI悦创,加我好友「不是小号哦」,我拉你进群。有问题可以直接在群里直接提问,也可以并且 @我。我有时间并看到了,是肯定回你哒。「不推荐私聊看,因为你遇到的问题,有可能恰好其他人也遇到过,不要害羞,一起交流学习。这条信息一直有效,欢迎你来撩小编哦!『skr~』
1. 数据分析基础
也就是我们来看看,数据分析当中最底层的东西——数组「Array」,这也是其中最关键的概念,所以接下来我们来看看数组的概念。
什么是数组?
简单说就是有序的元素序列。比如列表 [1,2,3,4] ,这个是简单的一维数组,只有 4个元素,并且不能被拆分为其他的数组组合;复杂一点呢, [[1,2,3],[4,5,6]] 是一个二维数组,由两个一维数组组成。
有同学说,数组这东西不知道是什么东西,其实很简单:把数字编成组,当然它这一组数字肯定有不同的方式进行排列。我们可以看到下图:1D、2D、3D 是什么意思?其实也就是:一维数组、二维数组、三维数组。
所以,也就是说,我们对数字进行排列的时候我可以以一维的方式进行排列,那一维的长啥样呢?也就是下图的左边第一个图。那二维的呢?有点像个表格,也就是下图的中间「第二个图」。三维的就变成了这样的立方体,也就是下图的最右边的图形。
 image-20200804160433579
image-20200804160433579
所以,这样大家看上图基本上可以看出来是什么意思:
一维的数组它就只有一个方向;
二维的数组它就是两个方向;
三维的数组自然也就是三个方向「也就是在二维的基础上加了一个方向」;
2. 数据处理的一般流程
 image-20200804161848844
image-20200804161848844
接下来,我们来看看我们对于数据分析一般来说会有怎样的流程,一般来说会有如上所示的四步:
数据收集 :第一步其实也是很重要的,也就是我们的数据从哪里来。
数据预处理 :在正式处理数据之前,我们要做数据预处理。那有同学可能会问:预处理和处理有什么区别?
数据处理这一步呢,是我正式的要对数据进行处理和分析。预处理,它的作用是为了方便我们在第三部数据处理而做的数据预处理。
数据展示 :到这里也就是,我数据处理和分析完成了,我如何来把我们分析得出来的结果更加直观。
1. 数据收集
数据收集有如下几种常用的方法:
网络爬虫:可以自己写爬虫代码,自由度较高,麻烦的就是自己得写爬虫;
公开数据:比如一些新闻数据、微博评论数据等等一些可以为你提供下载的数据集;
购买数据:有专门的爬虫公司,可以为你的需求进行编写特定代码获取数据;
公司内部直接提供:比如你是做运营的,利用数据分析给运营看见销售情况等等;
其他渠道获取数据:调查问卷等其他形式;
2. 数据预处理
这里我简单的给大家列一下,不理解也是没有关系的:
归一化
二值化
维度变换
去重
无效数据过滤
1. 归一化
归一化方法有两种形式,一种是把数变为(0,1)之间的小数,一种是把有量纲表达式变为无量纲表达式。主要是为了数据处理方便提出来的,把数据映射到0~1范围之内处理,更加便捷快速,应该归到数字信号处理范畴之内。
把数变为(0,1)之间的小数
例1 :{2.5 3.5 0.5 1.5} 归一化后变成了 {0.3125 0.4375 0.0625 0.1875}
解:
2.5+3.5+0.5+1.5 = 8,
2.5/8 = 0.3125,
3.5/8 = 0.4375,
0.5/8 = 0.0625,
1.5/8 = 0.1875.
这个归一化就是将括号里面的总和变成1.然后写出每个数的比例。
1.1 无量纲表达式「选看」
归一化是一种简化计算的方式,即将有量纲的表达式,经过变换,化为无量纲的表达式,成为纯量。
在统计学中,归一化的具体作用是归纳统一样本的统计分布性。归一化在0-1之间是统计的概率分布,归一化在-1--+1之间是统计的坐标分布。
归一化化定义 :归一化就是要把需要处理的数据经过处理后(通过某种算法)限制在你需要的一定范围内。
首先归一化是为了后面数据处理的方便,其次是保证程序运行时收敛加快。
归一化的具体作用是 归纳统一样本的统计分布性 。
归一化在 0-1之间是 统计的概率分布 ,归一化在某个区间上是 统计的坐标分布 。
归一化有同一、统一和合一的意思。
如果是区间上的值,则可以用区间上的相对位置来归一化,即选中一个相位参考点,用相对位置和整个区间的比值或是整个区间的给定值作比值,得到一个归一化的数据,比如类似于一个概率值0<=p<=1;
如果是数值,则可以用很多常见的数学函数进行归一化,使它们之间的可比性更显然,更强,比如对数归一,指数归一,三角or反三角函数归一等,归一的目的:可能是使得没有可比性的数据变得具有可比性 ,但又还会保持相比较的两个数据之间的相对关系,如大小关系,大的仍然大,小的仍然小,或是为了作图,原来很难在一张图上作出来,归一化后就可以很方便的给出图上的相对位置等;
从集合的角度来看,可以做维度的维一,即抽象化归一,把不重要的,不具可比性的集合中的元素的属性去掉,保留人们关心的那些属性,这样,本来不具有可比性的对象或是事物,就可以归一,即归为一类,然后就可以比较了,并且,人们往往喜欢用相对量来比较,比如人和牛,身高体重都没有可比性,但身高/体重的值,就可能有了可比性,人吃多少,牛吃多少,可能也没有直接的可比性,但相对于体重,或是相对于一天的各自的能量提供需要的食量,就有了可比性;这些,从数学角度来看,可以认为是把有纲量变成了无纲量了。
数据标准化方法(Data Normalization Method)
数据处理之标准化/归一化,形式上是变化表达,本质上是为了比较认识 。数据的标准化是将数据按比例缩放,使之落入一个小的特定区间。由于信用指标体系的各个指标度量单位是不同的,为了能够将指标参与评价计算,需要对指标进行规范化处理,通过函数变换将其数值映射到某个数值区间。
2. 二值化
原图:
 img
img
二值化之后的效果:
 img
img
二值化(英语:Binarization)是图像分割的一种最简单的方法。二值化可以把灰度图像转换成二值图像。把大于某个临界灰度值的像素灰度设为灰度极大值,把小于这个值的像素灰度设为灰度极小值,从而实现二值化。
根据阈值选取的不同,二值化的算法分为固定阈值和自适应阈值。 比较常用的二值化方法则有:双峰法、P参数法、迭代法和**OTSU法**等。
二值化就是:我可能一堆数据,我们拿到手之后直接把它分成两类:低的跟高的,就类似于这样。
2.1 辅助理解
1. 图像分割
在计算机视觉领域,图像分割(segmentation)指的是将数字图像细分为多个图像子区域(像素的集合)(也被称作超像素)的过程。图像分割的目的是简化或改变图像的表示形式,使得图像更容易理解和分析。[1]图像分割通常用于定位图像中的物体和边界(线,曲线等)。更精确的,图像分割是对图像中的每个像素加标签的一个过程,这一过程使得具有相同标签的像素具有某种共同视觉特性。
图像分割的结果是图像上子区域的集合(这些子区域的全体覆盖了整个图像),或是从图像中提取的轮廓线的集合(例如边缘检测)。一个子区域中的每个像素在某种特性的度量下或是由计算得出的特性都是相似的,例如颜色、亮度、纹理。邻接区域在某种特性的度量下有很大的不同。[1]
2. 灰度
在计算机领域中,灰度(Gray scale)数字图像是每个像素只有一个采样颜色的图像。这类图像通常显示为从最暗黑色到最亮的白色的灰度,尽管理论上这个采样可以是任何颜色的不同深浅,甚至可以是不同亮度上的不同颜色。灰度图像与黑白图像不同,在计算机图像领域中黑白图像只有黑白两种颜色,灰度图像在黑色与白色之间还有许多级的颜色深度。但是,在数字图像领域之外,“黑白图像”也表示“灰度图像”,例如灰度的照片通常叫做“黑白照片”。在一些关于数字图像的文章中**单色图像**等同于灰度图像,在另外一些文章中又等同于黑白图像。
灰度图像经常是在单个电磁波频谱如可见光内测量每个像素的亮度得到的。
用于显示的灰度图像通常用每个采样像素8 bits的非线性尺度来保存,这样可以有256种灰度(8bits就是2的8次方=256)。这种精度刚刚能够避免可见的条带失真,并且非常易于编程。在医学图像与遥感图像这些技术应用中经常采用更多的级数以充分利用每个采样10或12 bits的传感器精度,并且避免计算时的近似误差。在这样的应用领域流行使用16 bits即65536个组合(或65536种颜色)。
3. 二值图像
二值图像是每个像素只有两个可能值的数字图像。人们经常用黑白、B&W、单色图像表示二值图像,但是也可以用来表示每个像素只有一个采样值的任何图像,例如灰度图像等。
二值图像经常出现在数字图像处理中作为图像掩码或者在图像分割、二值化和dithering的结果中出现。一些输入输出设备,如激光打印机、传真机、单色计算机显示器等都可以处理二值图像。
二值图像经常使用位图格式存储。
二值图像可以解释为二维整数格 Z2,图像变形处理领域很大程度上就是受到这个观点启发。
3. 维度变换
可以理解为,二维变一维数组这样的变换。
4. 去重
如果重复的数据较多,我们可以在数据预处理的时候处理掉。
5. 无效数据过滤
有可能数据缺漏不全之类的。
3. 数据处理
数据排序:类似从大到小排序;
数据查找:按某种条件进行查找;
数据统计分析
这里其实有很多,我只是列了几个而已。
4. 数据展示
列表
图表
动态交互图形
以上就是数据处理的基本流程。
3. 为什么使用 Numpy
高性能
开源
数组运算
读写迅速
简单来讲,Python 内置的若干种数据类型,无法高效地应对计算密集型场景,比如矩阵运算。因此 Numpy 随之应运而生,并被认为是高性能科学计算和数据分析的基础包。
数据分析中所介绍到几乎所有的高级工具,都是基于 Numpy 开发的。因为 NumPy 的大部分代码都是用 C 语言写的,其底层算法在设计时就有着极优异的性能,所以使得 NumPy 比纯 Python 代码高效得多。作为基础工具,其实玩转 Numpy 很简单,只要掌握三个关键知识点,即:数据类型的创建、数据层的索引切片、数组运算。下面我们分不同的篇幅一一展开。
对于新入门的同学,尤其需要注意的是,虽然大多数的数据分析工作并不会直接操作 Numpy 对象,但是深谙面向数组的编程方式和逻辑能力是成为 Python 数据分析大牛的关键,切记磨刀不误砍柴工。
面向数组的编程方式,最大的特点就是用数组表达式完成数据操作任务,无需写大量循环。向量化的数组操作会比纯 Python 的等价实现快一到两个数量级。在后续的学习中,我们会有机会细细品味其中的差别和优势。
1. 高性能
import numpy as np
import time
list_array = list(range(int(1e6))) # 10 的 6次方
start_time = time.time()
python_array = [val * 5 for val in list_array] # 一百万个数字,里面每个数字都乘于 5
end_time = time.time()
print('Python array time: {}ms'.format(round((end_time - start_time) * 1000, 2)))
np_array = np.arange(1e6)
start_time = time.time()
np_array = np_array * 5
end_time = time.time()
print('Numpy array time: {}ms'.format(round((end_time - start_time) * 1000, 2)))
print('What sup!')
4. 安装 Numpy
Windows 系统: pip install numpy
Mac 系统: pip3 install numpy
5. 使用 Numpy 模块
5.1 新建一个 Python 文件
导入 Numpy 模块
import numpy as npas np表示在接下来的程序里 用 np 表示 numpyimport 某某模块 as 一个缩写
5.2 Numpy 的基础类型——ndarray
Numpy 最重要的一个特点就是它可以快速地创建一个 N 维数组对象(即 ndarray ,本文在 ndarray 对象和 数组 并不做概念上的区分),然后你可以利用 ndarray 这种数据结构非常高效地执行一些数学运算,并且语法风格和 Python 基本一致。
1. 创建数组
1. 一维数组
创建一个 ndarray 数组,我们在 Python 里面直接创建数组原本是这样创建的:
data = [2, 4, 6.5, 8]
创建 ndarray 最简单的方法就是使用 array 函数,它接受一个序列型对象(比如列表),并转化为 ndarray 对象。所以,如果要创建一个 Numpy 类型的 一维数组 ,就需要如下编写代码:
data = np.array([2, 4, 6.5, 8]) # np.array() 里面直接填一个由数字组成的列表
当然,你有可能想把列表单独的来写,那就可以像下面这么来写:
In [14]: python_list = [2, 4, 6.5, 8]
...: data = np.array(python_list)
In [15]: data
Out[15]: array([2. , 4. , 6.5, 8. ])
这里细心的朋友会发现一个有趣的现象,我们传入的列表中,存在 float 和 int 两种数据类型,但是在创建的 ndarray 对象中,默认转化为了 float 结构,这是因为 ndarray 是一个通用的同构数据多维容器,也就是说,其中的所有的元素必须是相同的类型, Numpy 会根据输入的实际情况进行转换。「也就是如果创建的时候,没有指定数据类型,那 Numpy 就会以数组中最小的数据类型为数据。」
2. 二维数组
上面我们创建了一个一维数组,接下来我们来创建一个 二维数组,有行有列的,我们是如下去创建的:
import numpy as np
data = np.array([[1, 2, 3], [4, 5, 6]]) # 也可以这么写:data = np.array([(1, 2), (3, 4)])
当然,我们的格式还可以这么写:「更加清晰一些」
import numpy as np
data = np.array(
[
[1, 2, 3],
[4, 5, 6]
]
)
Ps:嵌套列表或者嵌套元祖都是可以的,输出结果可以自行尝试。
这里我再次创建一个二维数组,并为同学们添加上了一张图片,方便同学们理解。
#创建二维数组
arr2d=np.arange(9, dtype=np.float32).reshape(3,3)
显然,二维数组有两个维度的索引,映射到平面空间的话,二维数组的两个轴分别为 axis 0和 axis 1,Numpy 默认先对 axis 0 轴索引,再对 axis 1轴索引。(数组其实可以视作嵌套列表,通常把最外层的索引定义为 axis 0,依次往里递增,该规律对于高维数组也适用)
 图片描述
图片描述
细心的同学会发现上面,我使用了 dtype 那我来补充一下:
#判断数组的数据类型
data = np.array([1, 2, 3, 4, 5])
np.issubdtype(data.dtype, np.integer)
Out: True
##数组类型也可以用字符代码来指代,主要是为了保持与诸如 Numeric 之类的旧程序包的向后兼容性。一些文档可能仍引用这些文档,例如:
data = np.array([1, 2, 3], dtype='f') # 等价于:array([ 1., 2., 3.], dtype=float32) 我们建议改为使用 dtype 对象。
data
Out: array([1., 2., 3.], dtype=float32)
data.dtype
Out[13]: dtype('float32')
3. 三维数组
三维数组比二维数组多了一维。三维数组在图片领域比较常见,对于 RGB 三原色模式的图片,就是用 m×n×3 大小的数组来表示一张图片,其中 m 表示图片垂直尺寸, n 表示图片水平尺寸,3 表示三原色。那在 Python 中我们如何创建三维数组呢?
import numpy as np
data = np.array(
[
[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]
]
)
print(data.ndim)
4. 高维数组
通常在我们的数据分析领域,甚至在AI大数据领域,原始的输入层都是二维的,即每个样本是一维的(由n个指标去定义一个样本),样本集则是二维的;在图片识别领域,通常用到的原始输入层都是三维的,因为图片一般都是三维的数组。所以朋友们熟悉二维和三维的常用索引、切片就足够应付绝大部分实际场景了。高维数组不建议大家深入挖掘。
四维数组
import numpy as np
data = np.array(
[
[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]],
[[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]
]
)
print(data.ndim)
五维数组
import numpy as np
data = np.array(
[
[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]],
[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]]
]
)
print(data.ndim)
六维数组
import numpy as np
data = np.array(
[
[[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]],[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]]],
[[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]],[[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]], [[[13, 14, 15], [16, 17, 18]], [[19, 20, 21], [22, 23, 24]]]]],
]
)
print(data.ndim)
其他维度的数组可以自行尝试,没写出来不代表没有!自己试一试才知道!
2. arange 创建等差数组
如果让大家创建一个等差列表,从1到100,一共 100 项,那一定非常方便,用 range(1,101,1) 快速搞定。Numpy 也提供了类似的方法 arange() ,用法与 range() 非常相似。
In [1]: import numpy as np
...: # 指定 start、stop、以及step。arange和range一样,是左闭右开的区间。
...: arr_uniform0 = np.arange(1,10,1)
...: # 也可以只传入一个参数,这种情况下默认start=0,step=1
...: arr_uniform1 = np.arange(10)
In [2]: arr_uniform0
Out[2]: array([1, 2, 3, 4, 5, 6, 7, 8, 9])
In [3]: arr_uniform1
Out[3]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
3. ndmin 指定创建的数组类型
'''
Minimum dimensions 2:
最小尺寸2:
Notes:ndmin: 指定维度类型,类似强制转换
'''
# 示例一:
import numpy as np
data = np.array([1, 2, 3], ndmin=2)
print(data)
print(data.ndim)
# 输出结果:
[[1 2 3]]
2
# 示例二:
import numpy as np
data = np.array([1, 2, 3], ndmin=3)
print(data)
print(data.ndim)
# 输出结果:
[[[1 2 3]]]
3
4. 判断 ndarray 维度「判断数组维度」——ndim
ndim = property(lambda self: object(), lambda self, v: None, lambda self: None) # default
"""Number of array dimensions.
数组维数。
Examples
--------
>>> x = np.array([1, 2, 3])
>>> x.ndim
1
>>> y = np.zeros((2, 3, 4))
# np.zeros((组,行,列)) 三维
# np.zeros((行,列)) 二维
>>> y.ndim
3
"""
其实,上面的代码已经用到了 ndim ,这个可以帮助我们查看数组维度,有时候肉眼也不一定看的清楚,其次就是你的数组来源有可能是其他方式的来源,用 ndim 就会更加的智能化。
import numpy as np
data = np.array(
[
[1, 2, 3],
[4, 5, 6]
]
)
print(data.ndim)
5. 了解 ndarray 各维度的长度
我不仅要知道这个数组有多少维度,我们还想知道该数组在每个维度上面的长度是多少。 比如:我们有个二维数组,我们想要知道,这个二维数组是几行几列。「每个维度的长度」
import numpy as np
data = np.array(
[
[1, 2, 3],
[4, 5, 6]
]
)
print(data.shape)
运行结果:
(2, 3) # 两行三列
当然,我们不仅仅可以使用 shape 查看数组各维度的长度,还可以使用它变换数组的维度:
import numpy as np
data = np.array(
[
[1, 2, 3],
[4, 5, 6]
]
)
print(f"原本数组的维度:{data.ndim}")
data.shape = (6,)
print(data)
print(f"变换之后,数组的维度:{data.ndim}")
6. 创建全是 0 的数组
比如,我想初始化一个全是 0 的数组,先暂时的创建全是 0 的数组。
import numpy as np
data = np.zeros(10)
print(data)
运行结果:
[0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
上面的 0. 实际是 0.0
补充内容:
import numpy as np
data = np.zeros((2, 3, 4))
# np.zeros((组,行,列)) 三维
# np.zeros((行,列)) 二维
print(data)
print(data.ndim)
运行结果:
[[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]
[[0. 0. 0. 0.]
[0. 0. 0. 0.]
[0. 0. 0. 0.]]]
3
7. 创建一个全是 1 的二维数组
看了小标题之后,同学们会问:那创建全是 1 的一维数组呢?
import numpy as np
data = np.ones(10)
print(data)
# 运行结果
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
接下来,我们来创建全是 1 的二维数组:
import numpy as np
data = np.ones((3, 10))
# np.ones((组,行,列)) 三维
# np.ones((行,列)) 二维
print(data)
print(data.ndim)
运行结果:
[[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1.]]
2
创建全是 1 的三维数组:
import numpy as np
data = np.ones((2, 4, 6))
# np.ones((组,行,列)) 三维
# np.ones((行,列)) 二维
print(data)
print(data.ndim)
注意:多位数组的长度需要使用元组来表示。
8. 数组的索引与切片
1. 获取数组中的某个数字(行话:索引)
import numpy as np
data = np.arange(10)
print(data)
print(data[5])
# 输出
[0 1 2 3 4 5 6 7 8 9]
5
2. 获取二维数组中的某个数字(行话:索引)
import numpy as np
arr2d = np.arange(9, dtype=np.float32).reshape(3,3)
print(arr2d)
# 输出
[[0. 1. 2.]
[3. 4. 5.]
[6. 7. 8.]]
如果仅仅对axis 0轴进行索引:
# 方括号里面,可以理解为对轴的操作。这里方括号里为单个整数,表示对最外层的axis 0进行操作
print(arr2d[1])
# 结果请参考下图的左侧部分
[3. 4. 5.]
同时对axis 0轴和axis 1轴进行索引:
# 方括号里为2个整数,表示依次对axis 0和axis 1操作(axis 0在前);取同时满足axis 0中index=1和axis 1中index=1的元素
print(arr2d[1, 1])
# 结果请参考下图的右侧部分
4.0
 图片描述
图片描述
其他形式的索引方式:
# 行从 0 开始
print(arr2d[0][2]) # 2.0
print(arr2d[0, 1]) # 1.0
print(arr2d[1, 0]) # 3.0
3. 获取三维数组中的某个数字(行话:索引)
import numpy as np
data = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
# 行从 0 开始
# 变为三维数组
data.shape = (2, 2, 2)
print(data)
print(data.ndim)
print(data[0][0][1]) # 2
print(data[0, 0, 1]) # 2
这里使用转换而不是直接创建三维数组或者使用 reshape 是为了让小伙伴们知道除了使用 reshape 之外如何变换数组。
这里提前说一下 shape 和 reshape 在变换数组维度最主要的区别是:「shape」:一个是修改数组本身,「reshape」:一个是新建一个数组返回。
4. 获取一维数组中某几个数字(行话:切片)
在索引的基础上稍微拓展一下,同时选择多个连续的索引,那就是切片效果了。
import numpy as np
data = np.arange(10)
print(data) # [0 1 2 3 4 5 6 7 8 9]
print(data[3:6]) # [3 4 5]
切片起始位置是 0 的话可以省略不写
比如: data[:6] 和 data[0:6] 得到的结果一 样
5. 获取二维数组中某几个数字(行话:切片)
import numpy as np
arr2d = np.arange(9, dtype=np.float32).reshape(3,3)
print(arr2d)
print(arr2d[0][0:3])
print(arr2d[0, 0:3])
# 输出
[[0. 1. 2.]
[3. 4. 5.]
[6. 7. 8.]]
[0. 1. 2.]
[0. 1. 2.]
上面我给大家展示的是最最简单的切片,接下来我给大家来一点稍微进阶的内容。细细品味下面的操作:「下方为了方便阅读,使用 IPython 操作」
In [16]: arr2d=np.arange(9, dtype=np.float32).reshape(3,3)
In [17]: arr2d
Out[17]:
array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]], dtype=float32)
In [18]: arr2d[0]
Out[18]: array([0., 1., 2.], dtype=float32)
In [19]: arr2d[0:2, 1:3]
Out[19]:
array([[1., 2.],
[4., 5.]], dtype=float32)
In [20]: arr2d[0:2][1:3]
Out[20]: array([[3., 4., 5.]], dtype=float32)
In [21]: arr2d=np.arange(12, dtype=np.float32).reshape(4,3)
In [22]: arr2d
Out[22]:
array([[ 0., 1., 2.],
[ 3., 4., 5.],
[ 6., 7., 8.],
[ 9., 10., 11.]], dtype=float32)
In [23]: arr2d[0:2, 1:3]
Out[23]:
array([[1., 2.],
[4., 5.]], dtype=float32)
In [24]: arr2d[0:3, 1:2]
Out[24]:
array([[1.],
[4.],
[7.]], dtype=float32)
In [25]: arr2d[0:3][1:2]
Out[25]: array([[3., 4., 5.]], dtype=float32)
In [26]: arr2d[0:3]
Out[26]:
array([[0., 1., 2.],
[3., 4., 5.],
[6., 7., 8.]], dtype=float32)
In [27]: arr2d[1:2]
Out[27]: array([[3., 4., 5.]], dtype=float32)
6. 获取三维数组中某几个数字(行话:切片)
import numpy as np
data = np.array([[1, 2, 3, 4], [5, 6, 7, 8]])
print(data.ndim) # 2
Three_dimensional_array = data.reshape(2, 2, 2)
print(Three_dimensional_array.ndim) # 3
# array([])[组][行][]
print(Three_dimensional_array[0][0][0:3]) # [1 2]
print(Three_dimensional_array[0][0][:]) # [1 2]
print(Three_dimensional_array[0][0]) # [1 2]
**注意!**切片得到的数据,对应的还是原始数据。任何修改都会反映到原始数据上。
import numpy as np
data = np.arange(10)
data_slice = data[3:6]
data_slice[2] = 100
print(f"data_slice:{data_slice}")
print(f"data:{data}")
# 输出
data_slice:[ 3 4 100]
data:[ 0 1 2 3 4 100 6 7 8 9]
想要一份副本不影响原始数据? 请用 data[3:6].copy()
import numpy as np
data = np.arange(10)
data_slice = data[3:6].copy()
data_slice[2] = 100
print(f"data_slice:{data_slice}")
print(f"data:{data}")
# 输出
data_slice:[ 3 4 100]
data:[0 1 2 3 4 5 6 7 8 9]
7. 布尔型索引
当数组碰到实际场景的时候,布尔型的索引就显得更接地气一点了。打个比方来说的话,布尔型索引更像 Excel 中的筛选器,基于条件判定结果的布尔值,来决定哪些数据是我们的目标数据。
我们先来看一个例子:
cities = np.array(["hz", "sh", "hz", "bj", "wh", "sh", "sz"])
arr_rnd = np.random.randn(7,4) # 创建一个符合 7x4 的正态分布的数组
arr_rnd
Out:
array([[ 0.52214772, 0.70276312, -2.2606387 , 0.44816176],
[ 1.8575996 , -0.07908252, -0.60976332, -1.24109283],
[ 0.79739726, 0.86862637, 0.91748762, 1.58236216],
[-2.01706647, 1.02411895, -0.27238117, 0.11644394],
[-0.5413323 , 0.41044278, -0.54505957, -0.27226035],
[ 0.85592045, 1.14458831, 0.36227036, -0.22211316],
[ 2.40476032, 1.22042702, -1.07018219, 0.95419508]])
# 利用数组的比较运算,生成一个布尔类型的数组
cities == "hz"
Out: array([ True, False, True, False, False, False, False])
# 利用布尔型数组,进行数组索引;观察索引的规律
# 我们可以做这样一个推断:布尔型数组的长度要和被索引的轴的长度一致
arr_rnd[cities == "hz"]
Out:
array([[ 0.52214772, 0.70276312, -2.2606387 , 0.44816176],
[ 0.79739726, 0.86862637, 0.91748762, 1.58236216]])
这里需要注意的是,布尔型索引可以和索引切片联用:
# 利用布尔型数组、切片进行2个维度的索引
arr_rnd[cities == "hz", :3]
Out:
array([[ 0.52214772, 0.70276312, -2.2606387 ],
[ 0.79739726, 0.86862637, 0.91748762]])
当然了,布尔型索引使用得恰到好处,具有化腐朽为神奇的功效。例如对于上一步生成的服从标准正态分布的arr_rnd数组,我希望能够把其中的负数都筛选出来,并置为0。其实非常简便:
arr_rnd[arr_rnd<0] = 0
arr_rnd
Out:
array([[0.52214772, 0.70276312, 0. , 0.44816176],
[1.8575996 , 0. , 0. , 0. ],
[0.79739726, 0.86862637, 0.91748762, 1.58236216],
[0. , 1.02411895, 0. , 0.11644394],
[0. , 0.41044278, 0. , 0. ],
[0.85592045, 1.14458831, 0.36227036, 0. ],
[2.40476032, 1.22042702, 0. , 0.95419508]])
在这里还需要强调一下布尔型数组的布尔算数运算符,有点绕口,但是其实很好理解,就是如何便捷地实现多个布尔型数组之间的“和”、“或”、“非”运算:
cities == "hz"
Out: array([ True, False, True, False, False, False, False])
cities == "sz"
Out: array([False, False, False, False, False, False, True])
# 非运算 ~
~(cities == "hz")
Out: array([False, True, False, True, True, True, True])
# 和运算 &
(cities == "hz") & (cities == "sz")
Out: array([False, False, False, False, False, False, False])
# 或运算 |
(cities == "hz") | (cities == "sz")
Out: array([ True, False, True, False, False, False, True])
8. 花式索引
简单总结一下,截止到这里,我们一共讲解了如何创建数组、一些常用的 Numpy 函数、以及数组运算,还有就是:如何利用单个整数、切片、布尔列表以及它们之间的组合来进行索引。事实上,它们已经很强大了,强大到足够应付绝大部分场景。我们来看一个案例,我有一个4×6的二维数组,我希望做一个有趣的切片,把二维数组4个角的元素取出来,组成一个2×2的数组,效果如下:
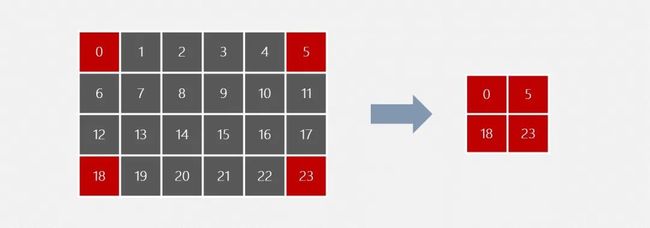 图片描述
图片描述
利用我们截止目前讲解到知识,也是可以实现的,只不过因为我们学到的都是连续的切片或者独立的单个索引,所以要实现这个效果会稍微繁琐一些。朋友们读到这里,不妨思考一下,你有什么方法来解决这个问题呢?
这里至少我们可以先提供2个思路:
# 新建4×6的二维数组arr_
arr_demo01 = np.arange(24).reshape(4,6)
arr_demo01
Our:
array([[ 0, 1, 2, 3, 4, 5],
[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17],
[18, 19, 20, 21, 22, 23]])
# 方法1:分别将4个角的元素索引出来,然后把取出来的4个元素,重新组成一个新2×2的数组
arr_method1 = np.array([[arr_demo01[0,0], arr_demo01[0,-1]],
[arr_demo01[-1,0],arr_demo01[-1,-1]]])
arr_method1
Out:
array([[ 0, 5],
[18, 23]])
# 方法2:利用布尔索引,可以同时索引不连续的行。分别对axis 0方向和axis 1方向进行索引。但是需要注意的是,得分2次索引;
arr_method2 = arr_demo01[[True, False, False, True]][:, [True, False, False, False, False, True]]
arr_method2:
Out:
array([[ 0, 5],
[18, 23]])
第一种方法更容易理解一些,第二种方法则是分别做两次索引。第一步是对axis 0方向进行布尔索引;第二步是综合运营切片和布尔索引,在上一步生成的结果上,对axis 1方向进行索引。
那有没有更简洁的方法呢?这里就要祭出花式索引了。
花式索引,其实就是利用整数数组来进行索引。基于上面我们生成的arr_demo01,我们来看两个简单的例子。
# 我们传入一个整数数组,对axis 0方向进行索引,并且索引结果的顺序和传入的整数数组一一对应:
arr_demo01[[2,0]]
Out:
array([[12, 13, 14, 15, 16, 17],
[ 0, 1, 2, 3, 4, 5]])
如果我们同时传入两个整数数组呢,那结果可能会和预料中的有些不一样,我们看下面这个例子:
# 如果同时传入2个整数数组,中间用逗号分开。那么这两个数组会以两两配对的形式,对元素进行索引。而并不是一个矩形状的索引区域!
arr_demo01[[0,-1], [0,-1]]
Out:
array([ 0, 23])
这里实际索引到的结果是(0, 0), (-1, -1)这两个坐标上的元素,注意不是矩形状的区域哦。那如何实现上面 demo 的效果呢?这里我们再介绍几种方法,供大家比对、学习。
方法3:把4个角的坐标都传进去就行了,整个思路和方法1很接近,不过写法更简洁一些:
# 方法3:分别传入4个角的坐标,请朋友们注意观察传入的2个整数数组的规律
arr_demo01[[0, 0, -1, -1], [0, -1, 0, -1]]
Out: array([ 0, 5, 18, 23])
arr_demo01[[0,0,-1,-1], [0,-1,0,-1]].reshape(2,2)
Out:
array([[ 0, 5],
[18, 23]])
注意观察能够发现,这种方式得到的数据只是一系列元素组成的一维数组,还需要我们额外通过reshape方法更改数据形状。
# 方法4:利用花式索引和切片混用,整体思路和方法2很相似。也是通过连续2次索引,得到一个矩形状的区域
arr_demo01[[0,-1]] [:,[0,-1]]
Out:
array([[ 0, 5],
[18, 23]])
最后给大家介绍一个索引器,利用np.ix_函数,把传入的两个一维整数数组,转为为一个用于选取元素的区域索引器。
# 方法5:利用函数np.ix_,构建矩形索引器:
arr_demo01[np.ix_([0,-1], [0,-1])]
Out:
array([[ 0, 5],
[18, 23]])
我们利用索引和切片的方法,可以随心所欲地变化数组的结构、提取其中的元素以及元素集合。
整体来看,索引可以分为4个类型:单个整数的索引、布尔索引、切片索引(和Python列表一致)以及整数数组。稍微复杂一些的,则是其中的组合索引,比如说其它索引与切片索引的组合。相信朋友们细细读懂上文的内容,必定能够掌握数据的索引方法。在日常的学习中,建议把这一篇文章当做案例一样的工具书,以逻辑理解为主,遇到问题来查阅即可,并不需要死记硬背。
数组的索引与切片是整个数据分析课程的基础内容,在之后的 Pandas 内容中,我们还会遇到切片和索引的问题,届时大家可以对照起来看,加深理解。
9. 变换数组的维度 reshape()
接下来我们就来编写代码感受感受:
import numpy as np
data = np.arange(10)
print(data)
print(data.reshape((2, 5)))
# 输出
[0 1 2 3 4 5 6 7 8 9]
[[0 1 2 3 4]
[5 6 7 8 9]]
这里,我得补充个知识点,也就是各位小伙伴平时会看见其他人代码的 reshape 中有 -1 这个参数,这个 -1 代表什么呢?
上面其实,演示了 reshape 的一般用法,接下来我将完整的用代码加语言来演示 -1 的奥妙之处。
**一般用法:**numpy.arange(n).reshape(a, b) 依次生成 n 个自然数,并且以 a 行 b 列的数组形式显示:
In [1]:
np.arange(16).reshape(2,8) #生成 16 个自然数,以 2 行 8 列的形式显示
Out[1]:
array([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15]])
特殊用法: mat (or array).reshape(c, -1) 必须是矩阵格式或者数组格式,才能使用 .reshape(c, -1) 函数, 表示将此矩阵或者数组重组,以 c 行 d 列的形式表示 ( -1 的作用就在此,自动计算 d:d=数组或者矩阵里面所有的元素个数/c, d必须是整数,不然报错)(reshape(-1, e) 即列数固定,行数需要计算):
In [1]: import numpy as np
In [2]: arr=np.arange(16).reshape(2,8)
In [3]: arr
Out[3]:
array([[ 0, 1, 2, 3, 4, 5, 6, 7],
[ 8, 9, 10, 11, 12, 13, 14, 15]])
In [4]: arr.reshape(4,-1) #将 arr 变成 4 行的格式,列数自动计算的 (c=4, d=16/4=4)
out[4]:
array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11],
[12, 13, 14, 15]])
In [5]: arr.reshape(8,-1) #将arr变成8行的格式,列数自动计算的(c=8, d=16/8=2)
out[5]:
array([[ 0, 1],
[ 2, 3],
[ 4, 5],
[ 6, 7],
[ 8, 9],
[10, 11],
[12, 13],
[14, 15]])
In [6]: arr.reshape(10,-1) #将 arr 变成 10 行的格式,列数自动计算的(c=10, d=16/10=1.6 != Int)
out[6]:
ValueError: cannot reshape array of size 16 into shape (10,newaxis)
10. 变换数组的维度或长度 resize()
reshape 变换数组维度是属于新建一个数组,resize 变换数组属于原地变换,当然 我们可以看出这个函数除了 re 之外还有个 size,所以 resize 也是可以变换数组长度的。
缩小数组:将数组展平(按数据存储在内存中的顺序),调整大小并调整形状:
import numpy as np
a = np.array([[0, 1], [2, 3]], order='C')
# C 按行
a.resize((2, 1))
print(a)
a = np.array([[0, 1], [2, 3]], order='C')
a.resize(2, 2)
print(a)
# 输出
[[0]
[1]]
[[0 1]
[2 3]]
import numpy as np
a = np.array([[0, 1], [2, 3]], order='F')
# F 按列
a.resize((2, 1))
print(a)
a = np.array([[0, 1], [2, 3]], order='F')
a.resize((2, 2))
print(a)
# 输出
[[0]
[2]]
[[0 1]
[2 3]]
扩大数组:如上所述,但是缺少的条目用零填充:「如果改变的长度超过原本数组的数量,那将会自动使用 0 填充」
import numpy as np
a = np.array([[0, 1], [2, 3]]) # 默认 order='C'
print(a)
a.resize((2, 3))
print(a)
# 输出
[[0 1]
[2 3]]
[[0 1 2]
[3 0 0]]
import numpy as np
a = np.array([[0, 1], [2, 3]], order="F")
print(a)
a.resize((2, 3))
print(a)
# 输出
[[0 1]
[2 3]]
[[0 1 0]
[2 3 0]]
虽然,上面的代码已经演示了,接下来的代码也就当作补充的简单演示:
import numpy as np
data = np.arange(10)
print(data)
print(data.resize((2, 5)))
那如果我们想让数组不被改变呢?可以使用引用数组即可达到该效果:「引用数组可防止调整大小...「也就是我们引用数组之后,即可防止数组被调整大小!」
import numpy as np
a = np.array([[0, 1], [2, 3]])
c = a
a.resize((2, 3))
print(a)
# 输出
Traceback (most recent call last):
File "/Users/apple/PycharmProjects/Coder/project.py", line 5, in
a.resize((2, 3))
ValueError: cannot resize an array that references or is referenced
by another array in this way.
Use the np.resize function or refcheck=False
ValueError:无法调整引用或被引用数组的大小。除非 refcheck 为假:
所以我们可以将代码修改如下:
import numpy as np
a = np.array([[0, 1], [2, 3]])
c = a
a.resize((2, 3), refcheck=False)
print(a)
# 输出
[[0 1 2]
[3 0 0]]
11. 矩阵转置
如果,你学了线性代数「矩阵」,应该会知道是什么了,比如你原本是两行五列的数据,我们使用 .T ,就会把刚刚的两行五列变成了五行两列。
不过,我还是在这里稍微列一下这个矩阵转置的数学知识:
 image-20200809171818976
image-20200809171818976
操作代码如下:
import numpy as np
a = np.arange(10)
print(a)
print(a.reshape(2, 5))
print(a.reshape(2, 5).T)
# 输出
[0 1 2 3 4 5 6 7 8 9]
[[0 1 2 3 4]
[5 6 7 8 9]]
[[0 5]
[1 6]
[2 7]
[3 8]
[4 9]]
12. empty 函数,创建一个空数组,只分配内存空间,但是不填充任何值
In [33]: # empty 函数返回值为未经过初始化的垃圾值
...: np.empty((2,3), dtype=np.int8)
Out[33]:
array([[0, 0, 0],
[0, 0, 0]], dtype=int8)
13. identity 函数,创建一个大小为 n×n 的单位矩阵(对角线为1,其余为0)
# identity函数原型如下:
np.identity(n, dtype=)
In [42]: # 创建一个大小为3×3的单位矩阵
...: np.identity(3, dtype=np.int8)
Out[42]:
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]], dtype=int8)
14. eye 函数,identity 的升级版本
# eye函数的原型如下:
np.eye(N, M=None, k=0, dtype=)
如果仅仅指定 N,则输出大小为 N×N 的方阵,功能与 identity 函数一致;如果同时指定 N 和 M ,则输出大小为 N×M 的矩形矩阵。K 为调节值,调节为 1 的对角线的位置偏离度。这里可以通过具体例子来体会一下:
In [44]: # 创建3×3的方阵
...: np.eye(N=3, dtype=np.int8)
Out[44]:
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1]], dtype=int8)
In [45]: # 创建3×4的矩形矩阵
...: np.eye(N=3, M=4, dtype=np.int8)
Out[45]:
array([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0]], dtype=int8)
In [46]: # 创建3×4的矩形矩阵,并且为1的对角线向右偏移1个单位。
...: np.eye(N=3, M=4, k=1, dtype=np.int8)
Out[46]:
array([[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]], dtype=int8)
In [47]: # 创建3×4的矩形矩阵,并且为1的对角线向右偏移2个单位。
...: np.eye(N=3, M=4, k=2, dtype=np.int8)
Out[47]:
array([[0, 0, 1, 0],
[0, 0, 0, 1],
[0, 0, 0, 0]], dtype=int8)
需要注意的是,k 值可以为负数。比如 k=-2,则表示:为1的对角线向左偏移2个单位。
5.3 数组运算,“懒人”必备
老子道德经有云:道生一,一生二,二生三,三生万物。说的是“道”创生万物的过程,即“道”生万物从少到多,从简单到复杂的一个过程。
衍生到我们的数学学习中来,我们学习了数据的创建,好比是“道生一,一生二”的过程,数组运算则蕴含了无穷的组合,有点类似“二生三,三生万物”的感觉。确实,数组运算,极大地拓展了我们使用数组来解决实际问题的能力,让我们有了掌控数组小宇宙的能力。
数组的运算看似很神秘,其实很简单,你不需要学习复杂的数学知识,在日常的使用中,跟普通的运算并无太大差别。
1. 数组与标量之间的运算
通常我们把单独的数叫做标量,数组可以直接与标量进行计算,计算逻辑会自动传播到数组的全部元素中。我们举几个简单的例子:
# 数组与标量的加法运算
import numpy as np
arr = np.array([[1,2,3], [4,5,6]])
arr + 5
Out:
array([[ 6, 7, 8],
[ 9, 10, 11]])
# 数组与标量的乘法运算
arr * 2
Out:
array([[ 2, 4, 6],
[ 8, 10, 12]])
# 数组与标量的除法运算,求数组中每个元素的倒数
1 / arr
Out:
array([[1. , 0.5 , 0.33333333],
[0.25 , 0.2 , 0.16666667]])
# 数组与标量的乘方运算,求数组中每个元素的平方
arr ** 2
Out:
array([[ 1, 4, 9],
[16, 25, 36]], dtype=int32)
# 求数组中每个元素的算术平方根
arr ** 0.5
Out:
array([[1. , 1.41421356, 1.73205081],
[2. , 2.23606798, 2.44948974]])
2. 数组的通用函数运算
ufunc 是 universal function 的缩写,是不是听起来就感觉功能非常强大?确如其名,它能对数组中每个元素进行函数操作。NumPy 中很多 ufunc 函数计算速度非常快,因为都是采用 C 语言实现的。通用函数 ufunc,就是能够对数组中的每个元素进行微操,也就是元素级的函数运算。
四则运算
最简单的通用函数就是数组与数组的四则运算。但是在进行数组的四则运算的时候,我们需要保证二者的维数一样「其实,经过我测试需要列数一样,行数不一样也可以进行计算」:
# 数组的减法:
arr - arr
Out:
array([[0, 0, 0],
[0, 0, 0]])
# 数组的乘法:
arr * arr
Out:
array([[ 1, 4, 9],
[16, 25, 36]])
需要注意的是,这里的乘法是表示数组对应位置的元素相乘,并不是高等数学上的矩阵的乘法。当然了数组的加法和除法规则都类似,这里不一一举例了。
事实上,Numpy 也封装了针对四则运算的函数,这里我们以数组的通用乘法为例,如下:
# 数组乘法的另一种写法,效果与*星号乘法一致:
np.multiply(arr, arr)
Out:
array([[ 1, 4, 9],
[16, 25, 36]])
总的来讲,Numpy 针对常见的数组之间的运算,做了一些函数封装,一起看一下:
| 函数 | 说明 |
|---|---|
| add | 计算两个数组的和 |
| subtract | 从第一个数组减去第二个数组 |
| multiply | 计算两个数组元素的乘积(不是矩阵乘法) |
| divide | 第一个数组元素除以第二个数组元素 |
| power | 第一个数组元素 A,第二个数组元素 B,计算 A^B |
| fmax | 计算两个元素各个位置上更大的那个 |
| fmin | 计算两个元素各个位置上更小的那个 |
add:计算两个数组的和
data = np.add(1.0, 4.0) data Out: 5.0 data1 = np.array([1, 3, 5, 7, 9]) data2 = np.array([2, 4, 6, 8, 10]) np.add(data1, data2) Out: array([ 3, 7, 11, 15, 19]) data1 = np.arange(9.0).reshape((3, 3)) data2 = np.arange(3.0) f"data1:{data1}" Out: 'data1:[[0. 1. 2.]\n [3. 4. 5.]\n [6. 7. 8.]]' f"data2:{data2}" Out: 'data2:[0. 1. 2.]' np.add(data1, data2) Out: array([[ 0., 2., 4.], [ 3., 5., 7.], [ 6., 8., 10.]])这里我就特意的提一下 divide:第一个数组元素除以第二个数组元素。说到 divide 就不得不提到另一个函数:true_divide 这里我要说的是,Python3 之后,这两个函数是等价的,阅读这两个函数的源码解析即可得知。
power:第一个数组元素 A,第二个数组元素 B,计算 A^B
import numpy as np data1 = np.array([2, 6, 5]) data2 = np.array([1, 2, 3]) print(np.power(data1, data2)) print(data1 ** data2) print(np.power(data1, 2)) # 输出 [ 2 36 125] [ 2 36 125] [ 4 36 25]fmax:计算两个元素各个位置上更大的那个
import numpy as np data1 = np.array([2, 6, 5]) data2 = np.array([1, 2, 3]) print(np.fmax(data1, data2)) # 输出 [2 6 5] import numpy as np data = np.array([2, 6, 5]) print(np.fmax(data, 1)) print(np.fmax(data, 9)) # 输出 [2 6 5] [9 9 9]fmin:计算两个元素各个位置上更小的那个
import numpy as np data1 = np.array([2, 6, 5]) data2 = np.array([1, 2, 3]) print(np.fmin(data1, data2)) # 输出 [1 2 3] import numpy as np data = np.array([2, 6, 5]) print(np.fmin(data, 1)) print(np.fmin(data, 9)) # 输出 [1 1 1] [2 6 5]
根据通用函数所能接纳的参数的个数,我们常常又把通用函数分为一元函数和二元函数。
一元函数
对数组进行四舍五入是一个典型的一元函数,举例如下:
# 创建一个符合均值为5标准差为10的正态分布数组
arr_rnd = np.random.normal(5, 10, (3, 4))
arr_rnd
Out:
array([[19.03116154, 13.58954268, 11.93818701, 4.85006153],
[ 0.57122874, 4.33719914, 8.67773155, 10.15552974],
[ 7.04757778, 6.98288594, 10.60656035, 17.95555988]])
# 对数组进行四舍五入运算。需要注意的是,结果数组仍然保留了输入数组的 dtype 属性
np.rint(arr_rnd)
Out:
array([[19., 14., 12., 5.],
[ 1., 4., 9., 10.],
[ 7., 7., 11., 18.]])
对数组求三角函数、求平均、求幂运算等均输入一元函数的范畴,我们把常用的一元函数列举如下,供大家查阅:
| 函数 | 说明 |
|---|---|
| abs,fabs | 计算绝对值,对于非负数值,可以使用更快的fabs |
| sqrt,square,exp | 计算个元素的平方根、平方、指数e^x |
| log,log10,log2,log1p | 分别计算自然对数(底数为e)、底数为10的log、底数为2的 log、log(1+x) |
| sign | 计算各元素的正负号:1(整数)、0(零)、-1(负数) |
| ceil | 计算各元素的、大于等于该值的最小整数「向上取整」 |
| floor | 计算各元素的、大于等于该值的最大整数「向下取整」 |
| rint | 将各元素值四舍五入到最接近的整数,并保留 dtype |
| modf | 把数组的小数和整数部分以两个独立的数组分别返回 |
| isnan | 判断各元素是否为空 NaN,返回布尔型 |
| cos,cosh,sin,sinh,tan,tanh | 普通型和双曲型三角函数 |
abs:计算绝对值
data = np.array([1, -2, -4, 2]) print(data) # [ 1 -2 -4 2] print(np.abs(data)) # [1 2 4 2]sqrt:计算个元素的平方根
data = np.arange(10) print(np.sqrt(data)) # 输出 [0. 1. 1.41421356 1.73205081 2. 2.23606798 2.44948974 2.64575131 2.82842712 3. ]square:计算平方
data = np.array([1, -2, -4, 2]) print(data) # [ 1 -2 -4 2] print(np.square(data)) # [ 1 4 16 4]exp:计算指数e^x
data = np.array([1, -2, -4, 2]) print(data) # [ 1 -2 -4 2] print(np.exp(data)) # [2.71828183 0.13533528 0.01831564 7.3890561 ]sign:计算各元素的正负号:1(整数)、0(零)、-1(负数)
data = np.array([1, -2, -4, 2, 0, 100, -90]) print(data) # [ 1 -2 -4 2 0 100 -90] print(np.sign(data)) # [ 1 -1 -1 1 0 1 -1]ceil:计算各元素的、大于等于该值的最小整数「向上取整」
data = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) print(data) # [-1.7 -1.5 -0.2 0.2 1.5 1.7 2. ] print(np.ceil(data)) # [-1. -1. -0. 1. 2. 2. 2.]floor:计算各元素的、大于等于该值的最大整数「向下取整」
data = np.array([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) print(data) # [-1.7 -1.5 -0.2 0.2 1.5 1.7 2. ] print(np.floor(data)) # [-2. -2. -1. 0. 1. 1. 2.]isnan:判断各元素是否为空
NaN,返回布尔型data = np.array([-1.7, np.log(-1.), np.log(0), 1, 1.5, np.inf, np.nan]) data Out: array([-1.7, nan, -inf, 1. , 1.5, inf, nan]) np.isnan(data) Out: array([False, True, False, False, False, False, True]) # Inf = inf = infty = Infinity = PINF 无穷;无限大;无限距, np.inf : inf # np.log(-1.): nan # np.log(0) : -inf # np.nan : nan
二元函数
除了四则运算,对两个数组元素进行判断,是一个典型的二元函数,举例如下:
# 利用随机函数,产生2个数组
x = np.random.normal(5, 10, (3,1))
y = np.random.normal(5, 10, (3,1))
x
Out: array([ 9.5336068 , 8.31969942, 15.20601081])
y
Out: array([22.52827938, 3.01609475, 9.03514098])
# 计算,比较元素级的最大值
np.maximum(x,y)
Out: array([22.52827938, 8.31969942, 15.20601081])
# 计算,比较元素级的最小值
np.minimum(x,y)
Out: array([9.5336068 , 3.01609475, 9.03514098])
# 计算,执行元素级的比较
np.greater(x,y)
Out: array([False, True, True])
我们把常用的二元函数列举如下,供大家查阅:
| 函数 | 说明 |
|---|---|
| maximum,fmax | 计算元素级的最大值,fmax 自动忽略空值 NaN |
| minimum,fmin | 计算元素级的最小值,fmin 自动忽略空值 NaN |
| greater,greater_equal | 执行元素级的比较,生产布尔型数组。效果相当于>,≥ |
| less,less_equal | 执行元素级的比较,生产布尔型数组。效果相当于<,≤ |
| equal,not_equal | 执行元素级的比较,生产布尔型数组。效果相当于==,!= |
| logical_and,logical_or,logic_xor | 执行元素级的逻辑运算,相当于执行运算符&、|、^ |
这里要提醒朋友们的是,数组运算本身并不复杂,只是套用公式的过程。但是在使用之前,大家千万要注意数组中是否有空值,空值的存在可能会导致运算结果错误甚至是报错。判断数组是否存在空值,需要使用 isnan 函数。
3. 数组的线性代数运算
矩阵乘法
线性代数(例如矩阵乘法、矩阵分解、行列式以及其他数学函数)是任何数据分析库的重要组成部分。Numpy 也提供这样的能力,例如我们上面学习了若干中矩阵的元素级乘法,那么如何进行线性代数的乘法呢?其实很方便:
# 矩阵的乘法,输入的2个数组的维度需要满足矩阵乘法的要求,否则会报错;
# arr.T表示对arr数组进行转置
# np.dot表示对输入的两个数组进行矩阵乘法运算
np.dot(arr, arr.T)
Out:
array([[14, 32],
[32, 77]])
numpy.linalg 工具
numpy.linalg 中封装了一组标准的矩阵分解运算以及诸如逆运算、行列式等功能。我们一起简单看一下。
## 利用inv函数,求解矩阵的逆矩阵(注意:矩阵可变,首先必须是方阵)
# 第一步:导包
from numpy.linalg import inv
arr_lg = np.array([[0, 1, 2], [1, 0, 3], [4, -3 ,8]])
arr_lg
Out:
array([[ 0, 1, 2],
[ 1, 0, 3],
[ 4, -3, 8]])
arr_inv = inv(arr_lg)
arr_inv
Out:
array([[-4.5, 7. , -1.5],
[-2. , 4. , -1. ],
[ 1.5, -2. , 0.5]])
# 测试:矩阵与其本身逆矩阵相乘,结果应该为单位矩阵
np.dot(arr_lg, arr_inv)
Out:
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
numpy.linalg 中的函数 solve 可以求解形如 Ax = b 的线性方程组,其中 A 为矩阵,b 为一维数组,x 是未知变量。
# 求解如下方程组的解:
# x-2y+z=0
# 2y-8z=8
# -4x+5y+9z=-9
# 导入solve函数
from numpy.linalg import solve
A = np.array([[1, -2, 1], [0, 2, -8], [-4, 5, 9]])
b = np.array([0,8,-9])
X = solve(A,b)
X
Out:array([29., 16., 3.])
# 测试 AX=b
np.equal(np.dot(A, X), b)
Out: array([ True, True, True])
numpy.linalg 中还封装了一些其它函数,这里就不一一列举了,大家可以参考下表,根据需要选择合适的函数:
| 函数 | 说明 |
|---|---|
| diag | 以一维数组的形式返回方阵的对角线(或非对角线)元素,或将一维数组转换为方阵 |
| trace | 计算对角线元素的和 |
| det | 计算矩阵行列式 |
| eig | 计算方阵的本征值和本征向量 |
| inv | 计算方阵的逆 |
| pinv | 计算矩阵的 Moore-Penrose 伪逆 |
| qr | 计算 QR 分解 |
| svd | 计算奇异值分解(SVD) |
| solve | 解线性方程 |
| lstsq | 计算 Ax=b 的最小二乘解 |
4. 数组的聚合函数运算
聚合函数是指对一组值(比如一个数组)进行操作,返回一个单一值作为结果的函数,比如求数组所有元素之和就是聚合函数。常见的聚合函数有:求和,求最大最小,求平均,求标准差,求中位数等。
常用的聚合函数
常用的聚合函数一览表:
| 函数 | 说明 |
|---|---|
| sum | 计算数组所有元素的和「求和运算」 |
| mean | 计算数组所有元素的平均值「求均值」 |
| std | 计算数组所有元素的标准差 |
| min, max | 计算数组所有元素中的最小或最大值 |
| argmin, argmax | 计算数组所有元素中的最小或最大值对应的位置 |
| cumsum | 累积求和运算 |
| median | 求中位数 |
| var | 求方差 |
看着似乎挺简单,我们看一个案例,对arr_rnd进行求最大值:
arr_rnd = np.random.normal(5, 10, (3, 4))
np.max(arr_rnd)
Out: 19.324449336215558
但是在实际工程中,我们通常把若干个样本组成一个数组进行运算,比如arr_rnd的大小为3×4,我们可以将之视为由3个样本组成,每个样本是长度为4的水平向量。那么我希望对样本的4个维度为别求最大值,应该如何操作?
这里我们引入运算方向的概念。
Numpy 运算方向 axis 详解
为了简化问题,我们主要考虑二维数组的场景,毕竟这已经可以覆盖我们绝大部分的场景了。

在前面的内容中,为了可视化切片过程,我们把二维数组的垂直方向定义为 axis 0 轴,水平方向为 axis 1 轴。当我们在对 Numpy 进行运算时,我们把 axis=0 指定为垂直方向的计算, axis=1 指定为水平方向的运算。
那么,显然,如果我们希望解决上面的疑问,规定求最大值的方向为垂直方向即可,即 axis=0:
arr_rnd = np.random.normal(5, 10, (3, 4))
arr_rnd
Out:
array([[ 3.03935618, 10.4099711 , -2.52635821, 28.64354885],
[ 1.70071308, 12.09126794, -19.11971849, 16.37838998],
[ -0.49338333, 0.63231608, 17.84866128, 0.30924362]])
np.max(arr_rnd)
Out: 28.643548853069557
np.max(arr_rnd, axis=0)
Out: array([ 3.03935618, 12.09126794, 17.84866128, 28.64354885])
探究 argmin, argmax 原理
argmin, argmax:计算数组所有元素中的最小或最大值对应的位置
从最简单的例子出发
假定现在有一个数组 a = [3, 1, 2, 4, 6, 1] 现在要算数组 a 中最大数的索引是多少?
这个问题对于刚学编程的同学就能解决,最直接的思路:先假定第 0 个数最大,然后拿这个和后面的数比,找到大的就更新索引:代码如下
a = [3, 1, 2, 4, 6, 1]
maxindex = 0
i = 0
for tmp in a:
if tmp > a[maxindex]:
maxindex = i
i += 1
print(maxindex) # 4
这个问题虽然简单,但却可以让同学们理解 argmax,那其实说到 argmax 就不得不说 argmin 其实原理也是一样的,这里我把它的代码直接给出:
a = [3, 1, 2, 4, 6, 10]
minindex = 0
i = 0
for tmp in a:
if tmp < a[minindex]:
minindex = i
i += 1
print(minindex) # 1
解释
这里我 解释一下 argmax 而 argmin 就不解析了,基本类似。还是从一维数组出发,看下面的例子:
import numpy as np
a = np.array([3, 1, 2, 4, 6, 1])
print(np.argmax(a)) # 4
import numpy as np
a = np.array([3, 1, 2, 4, 6, 1, 6])
print(np.argmax(a)) # 4
argmax 返回的是最大数的索引 np.argmax 有一个参数 axis , 默认是 0,表示第几维的最大值。那如果我们要看二维的最大值的情况呢?(文章写到这里,我突然觉得使用 IPython 运行和演示代码真香,我就使用 IPython 演示代码)我们先来演示官方的示例代码:
In [2]: import numpy as np
In [3]: a = np.arange(6).reshape(2,3) + 10
In [4]: a
Out[4]:
array([[10, 11, 12],
[13, 14, 15]])
In [5]: np.argmax(a)
Out[5]: 5
In [6]: np.argmax(a, axis=0)
Out[6]: array([1, 1, 1])
In [7]: np.argmax(a, axis=1)
Out[7]: array([2, 2])
Ps: 在多次出现最大值的情况下,返回对应于第一次出现的索引。「In case of multiple occurrences of the maximum values, the indices corresponding to the first occurrence are returned.
5. 小试牛刀:面向数组的编程方式
经过上面的步骤,朋友们对数组极高的运算效率有了初步理解,利用 Numpy 中封装好的函数,可以省去我们写循环的繁杂步骤,我们把这种利用数组执行批量计算,而省去编写循环的过程,叫做矢量化。
利用函数解决一些问题
在实际应用中,我们面临的场景很可能不是一两个简单的函数能够解决的。比如投票,为了降低个人偏见的影响以保证比赛结果的客观公平,通常我们会去除一个最高分、去除一个最低分,并把剩下的打分的均值作为选手的最后成绩。
# 利用自带的随机数生成函数生成5位选手的评委打分结果,一共有7位评委。打分结果用5×7大小的数组表示
votes = np.random.randint(1, 10, (5, 7))
votes
Out: array([[8, 6, 4, 1, 6, 1, 5],
[7, 6, 1, 9, 2, 1, 5],
[9, 6, 8, 9, 3, 5, 4],
[8, 5, 8, 4, 7, 9, 7],
[6, 2, 1, 2, 1, 8, 3]])
# 总分-最高分-最低分,再求平均,即可求得最终结果
(np.sum(votes, axis=1)-np.max(votes, axis=1)-np.min(votes, axis=1))/5
Out: array([4.4, 4.2, 6.4, 7. , 2.8])
那么对于无法通过简单函数解决的呢?我们简单介绍两个方法:
利用 Numpy 实现条件判断
条件判断是在计算领域非常常见的一种场景。例如我希望对上面产生的 arr_rnd 的数据网格进行判断,如果数据元素小于等于5,则替换成 NaN。其实利用 np.where 函数轻松实现:
# where 函数中输入3个参数,分别是判断条件、为真时的值,为假时的值
# 在Numpy中,空值是一种新的数据格式,我们用np.nan产生空值
np.where(arr_rnd<5, np.nan, arr_rnd)
Out: array([[19.03116154, 13.58954268, 11.93818701, nan],
[ nan, nan, 8.67773155, 10.15552974],
[ 7.04757778, 6.98288594, 10.60656035, 17.95555988]])
np.frompyfunc
如果还是找不到合适的函数来实现自己的目的,那不妨自己写一个,也很简单。我们只需要利用. frompyfunc 函数,将计算单元素的函数转换成,能对数组的每个元素进行操作的函数即可。
举个简单栗子:
假设某淘宝店做批发生意,店里的人气产品 A 原价为 20元。
购买 100件及以上,打 6折;
购买 50件及以上,不到100件,打8折;
购买10件及以上,不满50件,打9折;
不满10件不打折。
已知某天 5位客户的具体购买量,求当天的营业额。方法有很多,那么今天这里给大家推荐一种基于数组的计算方法:
# 定义函数,购买x件订单,返回订单金额
def order(x):
if x>=100:
return 20*0.6*x
if x>=50:
return 20*0.8*x
if x>=10:
return 20*0.9*x
return 20*x
# frompyfunc函数有三个输入参数,分别是待转化的函数、函数的输入参数的个数、函数的返回值的个数
income = np.frompyfunc(order, 1, 1)
# order_lst 为 5位顾客的下单量
order_lst = [600, 300, 5, 2, 85]
# 计算当天的营业额
np.sum(income(order_lst))
Out: 12300.0
学完了数组的运算,Numpy 的初阶内容基本学完了。本文主要是对数组运算中常用的函数做了系统的简介,包括:数组的通用函数、线性代数、聚合函数等,并有若干个实战 demo 供朋友们学习。
涉及的函数较多,在学习中大家切勿以死记硬背的心态介入学习。在数据分析学习阶段,应该是以理解加实践为主,至于函数太多记不住,那就交给时间去解决吧,用多了自然就记住了。对于偏门的函数,在应用的时候查阅即可。
6. 数组的排序
In [8]: data = np.array([1, 9, 3, 2, 7, 4, 5, 6, 8])
In [9]: data.sort()
In [10]: data
Out[10]: array([1, 2, 3, 4, 5, 6, 7, 8, 9])
5.4 ndarray 的存取
读取 txt 文件,我们先创建一个 txt 文件,保存为:data.txt 内容如下:
1,2,3,4,5,6,7,8,9
那我们读取的代码如下:
import numpy as np
data = np.genfromtxt('data.txt', delimiter=',')
print(data)
以上的代码,就是简单的提取了一下,输出结果为浮点数,如果我们在读取之前就已经知道我们读取的数据是整数,我们可以有如下两种方法读取或者修改数据类型。
方法一:
data = np.genfromtxt('data.txt', dtype='int', delimiter=',')
方法二:
数组.astype(要转换成的类型)
data = np.genfromtxt('data.txt', delimiter=',')
print(data.astype(int))
genfromtxt 的方法较多建议同学们去阅读源码解析使用,这里就不赘述啦。
5.5 进阶必会:引用、拷贝与视图
一年一度的苹果手机发布大会,绝对会牢牢占据微博榜的热搜,虽然“槽点”不断,但是该买的还是得买,下手一点不心软。新款的iPhone Xs Max 终于顺利突破了天际,达到了12799元,不愧为神机。我们不妨遐想一下,今年年终奖发了100000大钞,决定犒劳一下自己和对象,各买了一个同样的苹果手机,配置、颜色、价格、甚至开机密码都设置为一样,绝对的情侣机。那么问题来了,这是两部完全一样的手机吗?
如果把我的手机定义为变量M, 那么对象的手机定义为N,那么如何判断二者是否一样呢?
M == N
如果用上述等于判断,那么结果肯定为 True 了。因为这个方法基于的是变量的内容,既然两部手机配置、颜色、功能等等都一样,那肯定是 True 。当然了,世界上没有两件完全一模一样的硬件配置,这点大家不要钻牛角。
M is N
如果用 is 判断呢?这个答案好像有点玄机,确实,答案应该是 False 。这里是基于同一性来判断的,即我的手机是不是你的手机?显然不是。
上面这个例子很好地解释了拷贝 copy 这个概念,即我的手机和对象的手机互为 copy ,但是我们不一样!
本文将从 Python 的引用、拷贝入手,并深入阐述 Numpy 的拷贝机理,协助大家在数据分析时,能够在数据处理的过程中,对数组变量与变量之间的联系,有更加深刻的认识。
1. Python 篇
Python 引用
对象的引用就是赋值的过程。我们举个栗子:
a = ["a", "b", "c"]
b = a
a is b
Out:
True
在上面的栗子里我们把a又重新赋值给 b,那么从 Python 内部机制来看,这个赋值的过程,其实只是又新建了一层引用(这里的引用,类似于指针的概念),建立了从 b 到真实的 list 数据的引用。该过程的原理图如下:
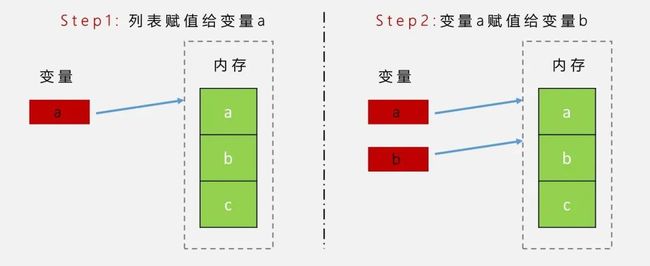 图片描述
图片描述
所以我么在用 is 比较 a 和 b 的时候,是比较其共同指向的同一块内存,同一性判断自然为 True。显然这里我们对 a 进行修改,b 会跟着变化,反之亦然。这就是引用的概念。
判断2个变量是否具有同一性,还可以用 id() 函数,该方法可以获取对象的内存地址。例如对上述的2个变量,我们可以做如下操作:
# 在具体的环境中进行内存地址查询时,地址编码一般情况下会不一样
# 但是深层次的规律是一样的,即a和b的内存地址相同
id(a)
Out: 1430507484680
id(b)
Out: 1430507484680
Python 的深拷贝与浅拷贝
在这之前,先放一个结论,数字和字符串中的内存都指向同一个地址,所以深拷贝和浅拷贝对于他们而言都是无意义的。也就是说,我们研究深拷贝和浅拷贝,都是针对可变对象进行研究,最常见的情况就是列表。
深拷贝
所谓的深拷贝,也就是基于被拷贝的可变对象,建立一个完全一样的拷贝后的对象,二者之间除了长得一模一样,但是相互独立,并不会互相影响。
我们以列表为例,举个单层常规列表的栗子:
# 对于单层常规列表,经过深拷贝操作后,拷贝后得到的对象的任何操作均无法改变原始对象
# Python的原生拷贝操作需要导入copy包,其中的deepcopy()函数表示深拷贝
import copy
m = ["Jack", "Tom", "Brown"]
n = copy.deepcopy(m)
我也附上示意图:
 image-20200815200123105
image-20200815200123105
# 判断二者是否相等,结果显而易见
m == n
Out: True
# 判断二者是否具有同一性,答案为否。也就是说,列表m和列表n是存储在不同的地址里。
m is n
Out: False
# 改变m首位的元素,发现n并无变化,说明二者互不影响
m[0] = "Helen"
m
Out: ['Helen', 'Tom', 'Brown']
n
Out: ['Jack', 'Tom', 'Brown']
上述案例说明,我们在对可变对象 m 使用深拷贝的时候,是完全复制了m的数据结构 ,并赋值给了n。这也符合我们直观上的认识。
浅拷贝
其实既然 Python 的 copy 有深浅之分,那显然浅拷贝必然有不一样的地方。如果只是针对由不可变的对象组成的单层常规列表,浅拷贝和深拷贝并无任何区别。这里我们简单做一下测试:
# 用copy库中的copy方法来表示浅拷贝
import copy
m = ["Jack", "Tom", "Brown"]
n = copy.copy(m)
# 判断浅拷贝前后是否具有同一性,答案是不具备同一性
m is n
Out: False
# 更改m的值,发现n并无任何变化。这里的规律保持和深拷贝一致
m[0] = "Black"
n
Out: ['Jack', 'Tom', 'Brown']
**那如果是嵌套列表呢?**会有一些不一样的地方。我们创建一个 2层列表,内存用长度为 3的列表表示学生的姓名、身高和体重;外层列表的首位表示班级:
# students列表的长度为3,其中首位为字符串,其他位均为列表
students = ["Class 1", ["Jack", 178, 120], ["Tom", 174, 109]]
students_c = copy.copy(students)
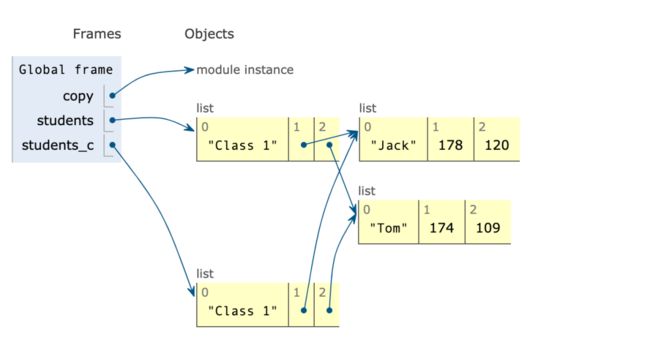 image-20200815200652509
image-20200815200652509
# 查看内嵌的列表是否具备同一性
students[1] is students_c[1]
Out: True
# 尝试更改students中某位学生的信息,通过测试更改后的students和students_c
students[1][1] = 180
students
Out: ['Class 1', ['Jack', 180, 120], ['Tom', 174, 109]]
students_c
Out: ['Class 1', ['Jack', 180, 120], ['Tom', 174, 109]]
## 发现:students_c也跟着改变了,这说明对于嵌套列表里的可变元素(深层次的数据结构),浅拷贝并没有进行拷贝,只是对其进行了引用
# 我们接着尝试更改students中的班级信息
students[0] = "Class 2"
students
Out: ['Class 2', ['Jack', 180, 120], ['Tom', 174, 109]]
students_c
Out: ['Class 1', ['Jack', 180, 120], ['Tom', 174, 109]]
## 发现:students_c没有发生变化,这说明对于嵌套列表里的不可变元素,浅拷贝和深拷贝效果一样
通过上述研究,我们能够得到如下结论:
1)由不可变对象组成的列表,浅拷贝和深拷贝效果一样,拷贝前后互相独立,互不影响;
2)当列表中含有可变元素时,浅拷贝只是建立了一个由该元素指向新列表的引用(指针),当该元素发生变化的时候,拷贝后的对象也会发生变化;
3)深拷贝完全不考虑节约内存,浅拷贝则相对来讲比较节约内存,浅拷贝仅仅是拷贝第一层元素;
切片与浅拷贝
通常来讲,我们对列表进行复制,切片是一种广泛且方便的操作,那么如果我们更改切片后得到的列表结构,会引起源列表的变化吗?
我们先上结论:切片其实就是对源列表进行部分元素的浅拷贝!
# 我们沿用上面的students列表的数据,通过对students进行切片等一系列微操作
students = ["Class 1", ["Jack", 178, 120], ["Tom", 174, 109]]
students_silce = students[:2]
# 对students的前2项进行切片,并赋值给students_silce;
# 修改students_silce的第二项,修改其中身高值,并比较源列表和切片结果的变化
students_silce[-1][1] = 185
students_silce
Out: ['Class 1', ['Jack', 185, 120]]
students
Out: ['Class 1', ['Jack', 185, 120], ['Tom', 174, 109]]
## 比较发现,切片结果的变化值,也传递给了源列表。说明可变元素的数据结构只是被引用,没有被复制。
# 修改students_silce的第一项,修改班级名,并比较源列表和切片结果的变化
students_silce[0] = "Class 3"
students_silce
Out: ['Class 3', ['Jack', 185, 120]]
students
Out: ['Class 1', ['Jack', 185, 120], ['Tom', 174, 109]]
# 比较发现,切片结果的变化值,没有传递给了源列表。说明对于不可变元素,切片前后互相独立。
## 综合比较,可以发现,切片的效果其实就是浅拷贝!
Python 的浅拷贝和深拷贝是理解 Python 原理的基础,深入理解二者的区别,对后续进阶、以及理解多维数组很有帮助。
2. Numpy篇
我们前面提到了,Numpy 为了适应大数据的特点,对内存做了优化。所谓的优化,就是以节约内存为前提,尽量在切片过程中减少对内存的开销。
对于 Numpy 来讲,我们主要甄别两个概念,即视图与副本。
(注意了,因为多维数组本可以视作嵌套列表,因此嵌套列表的浅拷贝的概念,在这里同样适用。其实多维数组视图的效果,可以理解为嵌套列表的浅拷贝。副本则和深拷贝的概念基本一致)
视图 view 是对数据的引用,通过该引用,可以方便地访问、操作原有数据,但原有数据不会产生拷贝。如果我们对视图进行修改,它会影响到原始数据,因为它们的物理内存在同一位置。
副本是对数据的完整拷贝( Python 中深拷贝的概念),如果我们对副本进行修改,它不会影响到原始数据,它们的物理内存不在同一位置。
view 视图
创建视图,我们可以通过两种方法:Numpy 的切片操作以及调用view() 函数。
我们先看一下利调用 view() 函数创建视图的案例:
# 视图是新建了一个引用,但是更改视图的维数,并不会引起原始数组的变化
import numpy as np
arr_0 = np.arange(12).reshape(3,4)
view_0 = arr_0.view()
view_0
Out: array([[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]])
# 从id看,二者并不具备同一性。
id(arr_0) is view_0
Out: False
# 更改视图的元素,则原始数据会产生联动效果
view_0[1,1] = 100
arr_0
Out: array([[ 0, 1, 2, 3],
[ 4, 100, 6, 7],
[ 8, 9, 10, 11]])
# 更改视图的维度:
# 视图的纬度更改并不会传递到原始数组
view_0.shape = (4,3)
print("arr_0 shape:", arr_0.shape, "view_0 shape:", view_0)
Out: arr_0 shape: (3, 4) view_0 shape: (4, 3)
利用切片创建视图朋友们都很熟悉了,我们来看一下在一维数组上测试的效果:
# 对一维数组切片,并对切片后的结果进行更改,查看是否对原始数组产生影响
arr_1 = np.arange(12)
slice_1 = arr_1[:6]
slice_1[3] = 99
slice_1
Out: array([ 0, 1, 2, 99, 4, 5])
# arr_1的第四个元素发生变成了99。在数组是1维的时候,规律和列表有些不一样,这里要特别注意。
arr_1
Out: array([ 0, 1, 2, 99, 4, 5, 6, 7, 8, 9, 10, 11])
副本
副本也就是深拷贝,相对而言对内存的处理比较粗暴,也比较好理解。建立副本前后,两个变量是完全独立的。
# Numpy建立副本的方法稍有不同。
# 方法一,是利用Numy自带的copy函数;
# 方法二,是利用deepcopy()函数。这里我们重点讲解方法一:
arr_2 = np.array([[1,2,3], [4,5,6]])
copy_2 = arr_2.copy()
copy_2[1,1] = 500
copy_2
Out: array([[ 1, 2, 3],
[ 4, 500, 6]])
arr_2
Out: array([[1, 2, 3],
[4, 5, 6]])
# 比较发现,建立副本后,二者互不影响。符合上面的结论。
这里讲解的知识点偏理论化一些,但是是朋友们从入门到进阶的过程中,必须要走的一步。如果初次阅读无法掌握,可以带着疑问,在后续的实践中一边实战,一边加深理解。
其实总结起来,主要是要区分直接赋值、浅拷贝和深拷贝这3个概念,其中的难点是理解浅拷贝概念。
浅拷贝在 Python 原生列表中,需要区分是否是嵌套列表。如果是嵌套列表,那么底层的列表和拷贝后的结果会随着一方的改变而改变。如果是由不可变元素组成的列表,那么浅拷贝与深拷贝并无区别。
浅拷贝在 Numpy 中则简单一些,无论数组的维数是多少,对视图或切片结果进行元素层面的修改时,操作的效果会反映到原始数组里。
5.6 对于 Numpy 的补充知识点
1. linspace()
上面的内容,完全可以带你学会并掌握 Numpy 这类库,接下来我来补充一些知识点:
linspace() 方法稍微复杂一些,它的函数调用参数如下:
np.linspace(start, stop[, num=50[, endpoint=True[, retstep=False[, dtype=None]]]]])
# start、stop 参数,和 arange() 中一致;
# num 为待创建的数组中的元素的个数,默认为50
# endpoint=True,则为左闭右闭区间,默认为 True;endpoint=False,则为左闭右开区间
# retstep 用来控制返回值的形式。默认为 False,返回数组;若为 True,则返回由数组和步长组成的元祖
简单看几个案例:
# 不设置 endpoint,默认为 Ture,结果为左闭右闭区间
In [43]: arr_uniform3 = np.linspace(1,99, 11)
In [44]: arr_uniform3
Out[44]: array([ 1. , 10.8, 20.6, 30.4, 40.2, 50. , 59.8, 69.6, 79.4, 89.2, 99. ])
# 设置 endpoint 为 False,结果为左闭右开区间
In [41]: arr_uniform4 = np.linspace(1,99, 11, endpoint=False)
In [42]: arr_uniform4
Out[42]:
array([ 1. , 9.90909091, 18.81818182, 27.72727273, 36.63636364,
45.54545455, 54.45454545, 63.36363636, 72.27272727, 81.18181818,
90.09090909])
# retstep 设置为 True,分别返回数组和步长
In [45]: arr_uniform5 = np.linspace(1,99, 11, retstep=True)
In [46]: arr_uniform5
Out[46]:
(array([ 1. , 10.8, 20.6, 30.4, 40.2, 50. , 59.8, 69.6, 79.4, 89.2, 99. ]),
9.8)
linspace() 方法最大的特点是可以直接定义数组的长度,这为我们调整数组的大小提供了方便。这里给大家介绍 reshape 方法「上面已经提到了 reshape 这里我就简单演示一下即可。」:
# 这里定义了一个长度为 20 的等差数组,然后通过 reshape 方法,调整数组的大小为5×4
In [49]: arr_uniform6 = np.linspace(1,100, 20)
In [50]: arr_uniform6.reshape(5,4)
Out[50]:
array([[ 1. , 6.21052632, 11.42105263, 16.63157895],
[ 21.84210526, 27.05263158, 32.26315789, 37.47368421],
[ 42.68421053, 47.89473684, 53.10526316, 58.31578947],
[ 63.52631579, 68.73684211, 73.94736842, 79.15789474],
[ 84.36842105, 89.57894737, 94.78947368, 100. ]])
reshape 方法非常灵活地应用于调整数组的大小,但是不改变数组的长度。即长度 100 的数组,你可以非常方便地调整为 1×100 或者是 4×25 或者是 5×20。这点在将横向量调整为列向量的时候非常有用。
2. 创建等比数组
等比数列在计算中也有着广泛的应用,比如说计算利率的时候。这里我们介绍两种方法创建等比数据。
geomspace() 方法,创建指数等比数列
比如说我想创建从 2 到 16 的等比数列,我不知道具体的公比,但是我希望我的数列长度是 4个。那我可以这样:
# 起始项为2,结束项为16,数列的长度为4。这里要注意,默认是左闭右闭的数组
In [51]: arr_geo0 = np.geomspace(2,16,4)
In [52]: arr_geo0
Out[52]: array([ 2., 4., 8., 16.])
geomspace() 方法非常简单,它的参数说明如下,以后用到,朋友们可以根据实际情况,自定义输入参数:
geomspace(start, stop, num=50, endpoint=True, dtype=None)
# start 和 stop,分别为区间的起始和终止值,为强制参数;
# num 为待生成等比数列的长度,指定后,程序会自动计算取等比数列的公比;
# endpoint默认为 True,结果为左闭右必区间。否则为 False,左闭右开区间;
logspace() 方法,创建对数等比数列
logspace() 方法和 geomspace() 类似,唯一不同的是,在定义区间的起始值和终止值的时候,是以指数的形式定义的,logspace() 用法如下:
logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)
# start:区间起始值为 base 的 start 次方
# stop:区间终止值为 base 的 stop 次方(是否取得到,需要设定参数 endpoint)
# num:为待生成等比数列的长度。按照对数,即 start 和 stop 值进行等分。默认值为 50
# endpoint:若为 True(默认),则可以取到区间终止值,即左闭右闭区间,规则同上
如果我们向生产和上面一样的等比数列,改如何写呢?
# 起始项为2^1,结束项为2^4,数列的长度为4。这里要注意,起始项是以base为底,start值为指数的幂。
# 另外,因为logspace的参数比较多,建议除了start和stop,其他的参数都以键值对的形式进行传参,避免发生错误
In [53]: arr_geo1 = np.logspace(1, 4, num=4, base=2)
In [54]: arr_geo1
Out[54]: array([ 2., 4., 8., 16.])
上面就是创建等比数列的全部内容了。窥一斑而知全豹,经过 Numpy 的封装,确实为我们提供很大的便利。这也正是 Python 做数据分析的魅力所在。
3. 创建随机数数组
随机数在编程世界里有很多妙用,比如我们都玩过的消消乐游戏,消掉一块后,屏幕顶端会自动下落一部分随机色块;还有欢乐玩斗地主的时候,洗牌就是一个随机的过程。
但是有的时候我们对生成的随机数也有一定的要求,比如我们在消消乐游戏里面,各个色块出现的概率是不一样的,特别是在高难度的关卡里,程序似乎可以故意提高“游戏难度”。其实这里的随机数都是经过缜密计算、精心设计的,那下面我们就来看看,如何生成一些“高阶”的随机数。
创建[0, 1)之间的均匀分布的随机数组
# 函数的输入为若干个整数,表示输出随机数的大小为 d0×d1× ...×dn
# 如果没有参数输入,则返回一个 float 型的随机数
numpy.random.rand(d0, d1, ..., dn)
# 产生一个大小为3×2,符合0-1之间的均匀分布的数组
In [57]: arr_rand0 = np.random.rand(3, 2) # 3 行 2 列
In [58]: arr_rand0
Out[58]:
array([[0.59348424, 0.30368829],
[0.73058467, 0.66220976],
[0.6186512 , 0.32079605]])
创建 [low, high) 之间的均匀分布的随机数组
# uniform 方法可以指定产生随机数的范围 [low, high),size 为数组的形状,输入格式为整形(一维)或者整形元祖
# 如果不指定size的话,则返回一个服从该分布的随机数
numpy.random.uniform(low=0.0, high=1.0, size=None)
# 产生一个大小为3×2,符合0-10之间的均匀分布的数组
arr_rand1 = np.random.uniform(1, 10, (3, 2))
arr_rand1
Out:
array([[6.72617294, 5.32504844],
[7.6895909 , 6.97631457],
[1.3057397 , 3.51288886]])
创建服从标准正态分布的数组(均值为0,方差为1)
# 该方法和rand类似,函数的输入为若干个整数,表示输出随机数的大小为d0×d1× ...×dn
# 如果没有参数输入,则返回一个服从标准正态分布的float型随机数
numpy.random.randn(d0, d1, ..., dn)
# 产生一个大小为3×2,符合标准正态分布的数组
arr_rand2 = np.random.randn(3, 2)
arr_rand2
Out:
array([[-0.70354968, -0.85339511],
[ 0.22804958, 0.28517509],
[ 0.736904 , -2.98846222]])
创建服从 μ=loc,σ=scale 的正态分布的数组
# loc:指定均值 μ; scale:指定标准差 σ
# size:输入格式为整形(一维)或者整形元祖,指定了数组的形状
numpy.random.normal(loc=0.0, scale=1.0, size=None)
# 产生一个大小为3×2,符合均值为5,标准差为10的正态分布的数组
arr_rand3 = np.random.normal(5, 10, (3, 2))
arr_rand3
Out:
array([[ -7.77480714, -2.68529581],
[ 4.40425363, -8.39891281],
[-13.08126657, -9.74238828]])
截止到现在,我们都是在产生某一区间或者符合某一规律的随机浮点数,那我们能不能随机产生整数呢?显然是可以的。
在指定区间 [low, high) 中离散均匀抽样的数组
# 函数返回区间[low, high)内的离散均匀抽样,dtype指定返回抽样数组的数据类型,默认为整形
# size:输入格式为整形(一维)或者整形元祖,指定了数组的形状
numpy.random.randint(low, high=None, size=None, dtype=np.int64)
# 在[1, 5)之间离散均匀抽样,数组形状为3行2列
arr_rand4 = np.random.randint(1, 5, (3, 2))
arr_rand4
Out:
array([[4, 4],
[3, 3],
[4, 2]])
对于 np.random.randint(1, 5, (3, 2)) 的执行结果,可以这样去理解:假设现有编号分别为1、2、3、4的4个小球,我们每次有放回抽样,分别抽样6次,把每次抽得的小球编号组合并调整为3×2大小的数组。
numpy.random.randint 可以非常方便地实现在某一整数区间内进行有放回的抽样,那如果我希望对具体实物进行抽样,有没有更好的方法呢?我们继续看。
对具体样本进行有放回或者无放回的抽样
# 从样本a中进行抽样,a可以为数组、列表或者整数,若为整数,表示[0,a)的离散抽样;
# replace为False,表示无放回抽样;replace为True,表示有放回抽样
# size为生成样本的大小
# p为给定数组中元素出现的概率
numpy.random.choice(a, size=None, replace=True, p=None)
我们看一个案例,小明同学在罚球线投篮命中的概率为0.65,总共投10次,我们看一下计算机的模拟结果:
# 因为理想情况下,每次投篮都不影响下一次的结果,所以把这个问题归结为有放回的抽样,一共进行10次
# shoot_lst用来存储投篮的结果
# 从["命中", "未命中"]中有放回抽样,其中命中的概率为0.65,共抽取10次,返回的格式为为numpy.ndarray
shoot_lst = np.random.choice(["命中", "未命中"], size=10, replace=True, p=[0.65, 0.35])
shoot_lst
Out: ['未命中', '命中', '未命中', '命中', '命中', '命中', '命中', '命中', '命中', '未命中']
从结果看,10次投篮,命中了3次。实际命中率在70%。当然了,如果计算机继续模拟,命中率会最终逼近65%。
4. 小试牛刀:采样的秘密
统计学是一门研究随机现象,以推断为特征的方法论科学,“由部分推及全体”的思想贯穿统计学的始终。
例如,有关部门每年都会发布在读大学生的身体素质报告,其中最基础的一项特征就是身高。那么这些身高是怎么来的呢?显然要获取全部在读大学生身高的成本是非常高的,所以为了降低成本,最简单的小窍门就是随机采样。那今天我们就来研究一下随机采样是如何能够反映样本的整体情况的。
通过查阅部分资料,我们知道大学生的身高都是服从某一正态分布规律的。
我们假设大学生平均身高是175厘米;
身高的标准差是10厘米;
那我们通过 Numpy 可以生成10万大学生的身高样本。我们本次的研究就是基于这10万样本,通过不断地采样,观察随着采样样本数的增多,其均值是如何变化的。我们用 numpy.random.choice 函数来模拟采样的过程。(程序会用到简单的 Numpy 的运算和matplotlib 的绘图功能,朋友们可以先了解一下,详细细节会在本课程的后续章节持续介绍。)
# 设置matplotlib图片样式在jupyter notebook中显示
%matplotlib inline
# 导包
import numpy as np
import matplotlib.pyplot as plt
# 生成10万大学生的身高样本
arr_height = np.random.normal(175, 10, size=100000)
# 进行第一次采样,采样的样本赋值给sample_height,存储格式为ndarray
sample_height = np.random.choice(arr_height, size=1, replace=True)
# average 用来存储每次采样后计算的平均身高
average = []
# 进行1000轮循环采样,因为每次仅采集1个样本,所以整个过程可以视为有放回抽样
n = 10000
for round in range(n):
sample = np.random.choice(arr_height, size=1, replace=True)
sample_height = np.append(sample_height, sample)
average.append(np.average(sample_height))
# 进行绘图,具体过程在数据可视化中会有详细的说明
plt.figure(figsize=(8,6))
plt.plot(np.arange(n), average, alpha=0.6, color='blue')
plt.plot(np.arange(n), [175 for i in range(n)], alpha=0.6, color='red', linestyle='--')
plt.xlabel("Sample Rounds", fontsize=10)
plt.ylabel("Average Height", fontsize=10)
plt.show()
 img
img
从图形可视化的效果看,在前 2000 次采样的过程中,采样样本的均值变化比较剧烈;但是随着样本数的增多,采样样本的均值越来越逼近175厘米。所以说,通过设置合理科学的采样方式,可以大大降低有关部门在日常统计工作的成本。
6. 案例
1. 数据归一化
下载数据
使用 NumPy,下载 iris 数据集。仅提取 iris 数据集的第二列 usecols = [1]
import numpy as np
url = 'https://images-aiyc-1301641396.cos.ap-guangzhou.myqcloud.com/Data_Analysis/iris.data'
wid = np.genfromtxt(url, delimiter=',', dtype='float', usecols=[1])
展示数据
array([3.5, 3. , 3.2, 3.1, 3.6, 3.9, 3.4, 3.4, 2.9, 3.1, 3.7, 3.4, 3. ,
3. , 4. , 4.4, 3.9, 3.5, 3.8, 3.8, 3.4, 3.7, 3.6, 3.3, 3.4, 3. ,
3.4, 3.5, 3.4, 3.2, 3.1, 3.4, 4.1, 4.2, 3.1, 3.2, 3.5, 3.1, 3. ,
3.4, 3.5, 2.3, 3.2, 3.5, 3.8, 3. , 3.8, 3.2, 3.7, 3.3, 3.2, 3.2,
3.1, 2.3, 2.8, 2.8, 3.3, 2.4, 2.9, 2.7, 2. , 3. , 2.2, 2.9, 2.9,
3.1, 3. , 2.7, 2.2, 2.5, 3.2, 2.8, 2.5, 2.8, 2.9, 3. , 2.8, 3. ,
2.9, 2.6, 2.4, 2.4, 2.7, 2.7, 3. , 3.4, 3.1, 2.3, 3. , 2.5, 2.6,
3. , 2.6, 2.3, 2.7, 3. , 2.9, 2.9, 2.5, 2.8, 3.3, 2.7, 3. , 2.9,
3. , 3. , 2.5, 2.9, 2.5, 3.6, 3.2, 2.7, 3. , 2.5, 2.8, 3.2, 3. ,
3.8, 2.6, 2.2, 3.2, 2.8, 2.8, 2.7, 3.3, 3.2, 2.8, 3. , 2.8, 3. ,
2.8, 3.8, 2.8, 2.8, 2.6, 3. , 3.4, 3.1, 3. , 3.1, 3.1, 3.1, 2.7,
3.2, 3.3, 3. , 2.5, 3. , 3.4, 3. ])
单变量(univariate),长度为 150 的一维 NumPy 数组。
归一化
求出最大值、最小值:
smax = np.max(wid)
smin = np.min(wid)
In [51]: smax,smin
Out[51]: (4.4, 2.0)
归一化公式:
s = (wid - smin) / (smax - smin)
归一化
Min-Max Normalization
x' = (x - X_min) / (X_max - X_min)
平均归一化
x' = (x - μ) / (MaxValue - MinValue)
(1)和(2)有一个缺陷就是当有新数据加入时,可能导致 max 和 min 的变化,需要重新定义。
非线性归一化
对数函数转换:y = log10(x)
反余切函数转换:y = atan(x) * 2 / π
经常用在数据分化比较大的场景,有些数值很大,有些很小。通过一些数学函数,将原始值进行映射。该方法包括 log、指数,正切等。需要根据数据分布的情况,决定非线性函数的曲线,比如log(V, 2)还是log(V, 10)等。
标准化
Z-score规范化(标准差标准化 / 零均值标准化)
x' = (x - μ)/σ
中心化
x' = x - μ
补充:数据分析——归一化「随笔」
还有一个更简便的方法,使用 ptp 方法,它直接求出最大值与最小值的差:
s = (wid - smin) / wid.ptp()
NumPy 的打印设置
只打印小数点后三位的设置方法:
np.set_printoptions(precision=3)
归一化结果:
array([0.625, 0.417, 0.5 , 0.458, 0.667, 0.792, 0.583, 0.583, 0.375,
0.458, 0.708, 0.583, 0.417, 0.417, 0.833, 1. , 0.792, 0.625,
0.75 , 0.75 , 0.583, 0.708, 0.667, 0.542, 0.583, 0.417, 0.583,
0.625, 0.583, 0.5 , 0.458, 0.583, 0.875, 0.917, 0.458, 0.5 ,
0.625, 0.458, 0.417, 0.583, 0.625, 0.125, 0.5 , 0.625, 0.75 ,
0.417, 0.75 , 0.5 , 0.708, 0.542, 0.5 , 0.5 , 0.458, 0.125,
0.333, 0.333, 0.542, 0.167, 0.375, 0.292, 0. , 0.417, 0.083,
0.375, 0.375, 0.458, 0.417, 0.292, 0.083, 0.208, 0.5 , 0.333,
0.208, 0.333, 0.375, 0.417, 0.333, 0.417, 0.375, 0.25 , 0.167,
0.167, 0.292, 0.292, 0.417, 0.583, 0.458, 0.125, 0.417, 0.208,
0.25 , 0.417, 0.25 , 0.125, 0.292, 0.417, 0.375, 0.375, 0.208,
0.333, 0.542, 0.292, 0.417, 0.375, 0.417, 0.417, 0.208, 0.375,
0.208, 0.667, 0.5 , 0.292, 0.417, 0.208, 0.333, 0.5 , 0.417,
0.75 , 0.25 , 0.083, 0.5 , 0.333, 0.333, 0.292, 0.542, 0.5 ,
0.333, 0.417, 0.333, 0.417, 0.333, 0.75 , 0.333, 0.333, 0.25 ,
0.417, 0.583, 0.458, 0.417, 0.458, 0.458, 0.458, 0.292, 0.5 ,
0.542, 0.417, 0.208, 0.417, 0.583, 0.417])
分布可视化:
import seaborn as sns
sns.distplot(s,kde=False,rug=True)
频率分布直方图:
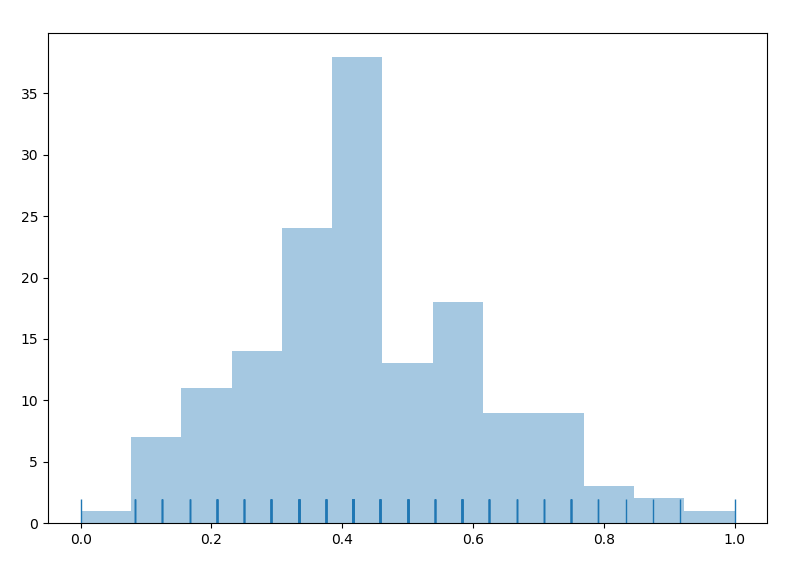 img
img
sns.distplot(s,hist=True,kde=True,rug=True)
带高斯密度核函数的直方图:
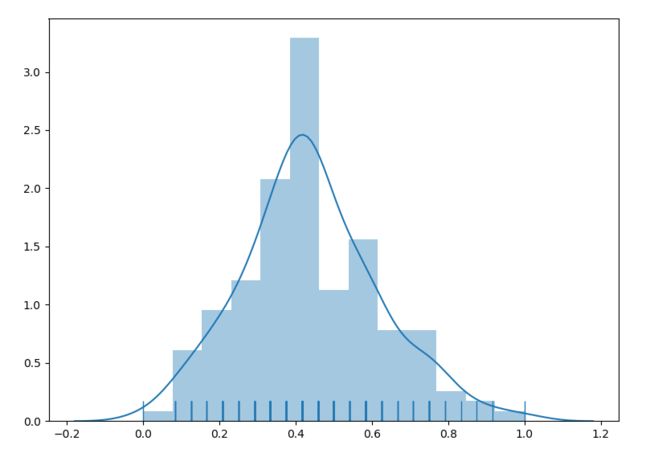 img
img
2. 11 道 NumPy 基础题
创建一个 [3,5] 所有元素为 True 的数组
In [1]: np.ones((3,5),dtype=bool)
Out[1]:
array([[ True, True, True, True, True],
[ True, True, True, True, True],
[ True, True, True, True, True]])
创建一个 [3,5] 所有元素为 False 的数组
In [2]: np.zeros((3, 5), dtype=bool)
Out[2]:
array([[False, False, False, False, False],
[False, False, False, False, False],
[False, False, False, False, False]])
一维数组转二维
In [3]: a = np.linspace(1,5,10)
In [4]: a.reshape(5,2)
Out[4]:
array([[1. , 1.44444444],
[1.88888889, 2.33333333],
[2.77777778, 3.22222222],
[3.66666667, 4.11111111],
[4.55555556, 5. ]])
数组所有奇数替换为 -1
In [5]: m = np.arange(10).reshape(2,5)
In [6]: m[m%2==1] = -1
In [7]: m
Out[7]:
array([[ 0, -1, 2, -1, 4],
[-1, 6, -1, 8, -1]])
提取出数组中所有奇数
In [8]: m = np.arange(10).reshape(2,5)
In [9]: m[m%2==1]
Out[9]: array([1, 3, 5, 7, 9])
2 个 NumPy 数组的交集
In [10]: m ,n = np.arange(10), np.arange(1,15,3)
In [11]: np.intersect1d(m,n)
Out[11]: array([1, 4, 7])
2 个 NumPy 数组的差集
In [12]: m ,n = np.arange(10), np.arange(1,15,3)
In [13]: np.setdiff1d(m,n)
Out[13]: array([0, 2, 3, 5, 6, 8, 9])
筛选出指定区间内的所有元素
注意:(m >2),必须要添加一对括号
In [14]: m = np.arange(10).reshape(2,5)
In [15]: m[(m > 2) & (m < 7)]
Out[15]: array([3, 4, 5, 6])
二维数组交换 2 列
In [16]: m = np.arange(10).reshape(2,5)
In [17]: m
Out[17]:
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
In [18]: m[:,[1,0,2,3,4]]
Out[18]:
array([[1, 0, 2, 3, 4],
[6, 5, 7, 8, 9]])
可以一次交换多列:
In [19]: m[:,[1,0,2,4,3]]
Out[19]:
array([[1, 0, 2, 4, 3],
[6, 5, 7, 9, 8]])
二维数组,反转行
In [20]: m = np.arange(10).reshape(2,5)
In [21]: m
Out[21]:
array([[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]])
In [22]: m[::-1]
Out[22]:
array([[5, 6, 7, 8, 9],
[0, 1, 2, 3, 4]])
生成数值 5~10、shape 为 (3,5) 的随机浮点数
In [9]: np.random.seed(100)
In [42]: np.random.randint(5,10,(3,5)) + np.random.rand(3,5)
Out[42]:
array([[9.31623868, 5.68431289, 9.5974916 , 5.85600452, 9.3478736 ],
[5.66356114, 7.78257215, 7.81974462, 6.60320117, 7.17326763],
[7.77318114, 6.81505713, 9.21447171, 5.08486345, 8.47547692]])
3. 练习题:统计全班的成绩
假设一个团队里有 5 名学员,成绩如下表所示。你可以用 NumPy 统计下这些人在语文、英语、数学中的平均成绩、最小成绩、最大成绩、方差、标准差。然后把这些人的总成绩排序,得出名次进行成绩输出。
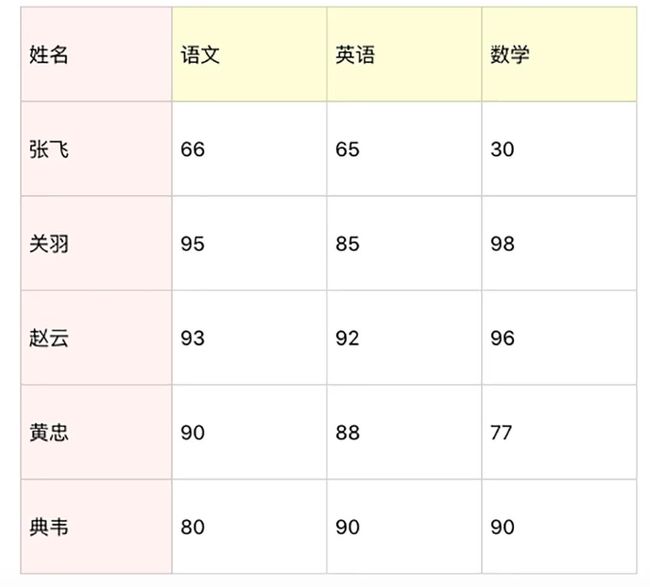 img
img
#!/usr/bin/python
#vim: set fileencoding:utf-8
import numpy as np
'''
假设一个团队里有5名学员,成绩如下表所示。
1.用NumPy统计下这些人在语文、英语、数学中的平均成绩、最小成绩、最大成绩、方差、标准差。
2.总成绩排序,得出名次进行成绩输出。
'''
scoretype = np.dtype({
'names': ['name', 'chinese', 'english', 'math'],
'formats': ['S32', 'i', 'i', 'i']})
peoples = np.array(
[
("zhangfei", 66, 65, 30),
("guanyu", 95, 85, 98),
("zhaoyun", 93, 92, 96),
("huangzhong", 90, 88, 77),
("dianwei", 80, 90, 90)
], dtype=scoretype)
#print(peoples)
name = peoples[:]['name']
wuli = peoples[:]['chinese']
zhili = peoples[:]['english']
tili = peoples[:]['math']
def show(name,cj):
print name,
print " |",
print np.mean(cj),
print " | ",
print np.min(cj),
print " | ",
print np.max(cj),
print " | ",
print np.var(cj),
print " | ",
print np.std(cj)
print("科目 | 平均成绩 | 最小成绩 | 最大成绩 | 方差 | 标准差")
show("语文", wuli)
show("英语", zhili)
show("数学", tili)
print("排名:")
ranking =sorted(peoples,cmp = lambda x,y: cmp(x[1]+x[2]+x[3],y[1]+y[2]+y[3]), reverse=True)
print(ranking)
7. 作业
统计书本的平均评分
读取文件 rating.txt 中的的数据并分析:https://aiyc.lanzous.com/iSU8ufj79af
https://www.aiyc.top/data-analysis-data-set
共有 10000 本书,以数字 id 表示
每个用户的打分为1~5
每一行数据有 3 个数字:分别表示用户 ID,书本 ID,该用户对该书的打分
要求输出: 所有书本各自的平均得分
作业解析
文件较大,没必要在测试的时候每次读取全部数据,我们可以创建个数据副本,数据少一些。
读取数据并转换为整数
import numpy as np
data = np.genfromtxt('rating.txt', delimiter=',')
data = data.astype(int)
print(data)
创建两个数组分别存放各个书籍的总评分和总评分人数
rating_sum = np.zeros(10000)
rating_people_count = np.zeros(10000)
For 循环读取每行的数据
for rating in data:
book_id = rating[1] - 1
rating_sum[book_id] += rating[2]
rating_people_count[book_id] += 1
第一列是用户的 ID 其实对于我们这道题目来说没什么用,所以我们不需要去管它。
这里我 rating[1] - 1 是为什么减去 1 呢?
同学们应该是知道的,编程中和数组的索引都是从 0 开始的,所以 减 1 就是为了可以直接使用书本的 ID 进行索引。
完整代码
import numpy as np
data = np.genfromtxt('rating.txt', delimiter=',')
data = data.astype(int)
# print(data)
rating_sum = np.zeros(10000)
rating_people_count = np.zeros(10000)
for rating in data:
book_id = rating[1] - 1
rating_sum[book_id] += rating[2]
rating_people_count[book_id] += 1
# 计算方法一:
result = rating_sum / rating_people_count
print(result)
# 计算方法二:
print(np.true_divide(rating_sum, rating_people_count))
# 输出
[4.27970709 4.35135011 3.21434056 ... 4.32352941 3.70769231 4.00900901]
[4.27970709 4.35135011 3.21434056 ... 4.32352941 3.70769231 4.00900901]
◆ ◆ ◆ ◆ ◆
号主新书相信可以帮助到大家入门数据分析,我写了本书:《拿下Offer-数据分析师求职面试指南》,恰逢当当网开学季活动,卧槽!当当网图书全场4折了!,详情如下:
当当网开学季活动来袭,满100减50的基础上,实付满200的基础上使用优惠码DYU6NM可以再减40,相当于400-240,
使用方法如下:
步骤一,挑选心仪的图书至购物车点击结算
步骤二,点击优惠券/码处
步骤三,输入优惠码DYU6NM (注意全部要大写)
需要注意的是:优惠码全场自营图书可用(教材、考试类除外)
![]()
更多详情可以扫描下方二维码:
![]()
点击阅读原文,即可参与当当400-240购书活动
