如何区分PCA PCoA NMDS LDA t-SNE?

PCA PCoA NMDS LDA t-SNE 理论理解与绘图

简介： 本文介绍PCA PCoA NMDS LDA t-SNE几种降维方法之间的差别，以及应用

一、基本概念

1. PCA

PCA（Principal Components Analysis）即主成分分析，也称主分量分析或主成分回归分析法，首先利用线性变换，将数据变换到一个新的坐标系统中；然后再利用降维的思想，使得任何数据投影的第一大方差在第一个坐标(称为第一主成分)上，第二大方差在第二个坐标(第二主成分)上。这种降维的思想首先减少数据集的维数，同时还保持数据集的对方差贡献最大的特征，最终使数据直观呈现在二维坐标系。
每一个点代表一个样本，相同颜色的点来自同一个分组，两点之间距离越近表明两者的群落构成差异越小。

2. PCoA

PCoA（Principal Co-ordinates Analysis）分析即主坐标分析，可呈现研究数据相似性或差异性的可视化坐标，是一种非约束性的数据降维分析方法，可用来研究样本群落组成的相似性或相异性。它与PCA类似，通过一系列的特征值和特征向量进行排序后，选择主要排在前几位的特征值，找到距离矩阵中最主要的坐标，结果是数据矩阵的一个旋转，它没有改变样本点之间的相互位置关系，只是改变了坐标系统。PCoA和PCA的区别为PCA是基于样本的相似系数矩阵（如欧式距离）来寻找主成分，而PCoA是基于距离矩阵（常用bray, jaccard, unifrac）来寻找主坐标。 PCoA以样本距离为整体考虑，更符合生态学数据特征，在微生物分析领域应用也更为广泛。

3. NMDS

非度量多维尺度分析(non-metric multi-dimensional scaling, NMDS)，是一种将多维控件的研究对象（样本或者变量）简化到低维空间进行定位/分析和归类，同时又保留对象原始关系的数据分析方法。其基本特征是将对象间的相似性或相异性数据堪称点间距离的单点函数，在保持原始数据次序关系的基础上，对其进行变量变换以数据列替换原始数据进行度量型多维尺度分析。在微生物16S或者宏基因组等分析流程中常见。NMDS与PCA分析的主要差异在于考量了进化上的信息，基于进化或者数量距离矩阵的数值来寻找主坐标。点与点之间距离越近表明两者的群落构成差异越小。

***划重点：PCA、PCaA 和NMDS都是无监督的，而LDA和t-SNE是有监督的。

4. LDA

线性判别分析（Linear Discriminant Analysis，LDA）也叫Fisher线性判别（Fisher Linear Discriminant），最初由Fisher于1936年提出Fisher线性判别，后来于1948年，改进成如今的LDA。

LDA的思想可以用一句话概括，就是“投影后类内方差最小，类间方差最大”。什么意思呢？ 我们要将数据在低维度上进行投影，投影后希望每一种类别数据的投影点尽可能的接近，而不同类别的数据的类别中心之间的距离尽可能的大。

可能还是有点抽象，我们先看看最简单的情况。假设我们有两类数据 分别为红色和蓝色，如下图所示，这些数据特征是二维的，我们希望将这些数据投影到一维的一条直线，让每一种类别数据的投影点尽可能的接近，而红色和蓝色数据中心之间的距离尽可能的大。

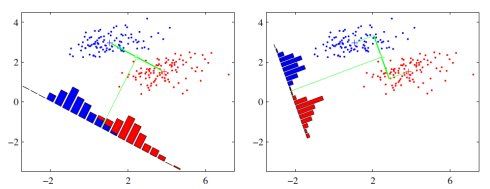
上图中提供了两种投影方式，哪一种能更好的满足我们的标准呢？从直观上可以看出，右图要比左图的投影效果好。因为右图的黑色数据和蓝色数据各个较为集中，且类别之间的距离明显，而左图则在边界处数据混杂。以上就是LDA的主要思想了，当然在实际应用中，我们的数据是多个类别的，我们的原始数据一般也是超过二维的，投影后的也一般不是直线，而是一个低维的超平面。

pca与lda的区别：
a、pca是无监督学习，lda是监督学习方法；
b、pca从协方差矩阵考虑，lda从类别矩阵和类内方差考虑；
c、pca降维后是n-1维，lda是类别数量-1维；
d、pca从协方差矩阵出发，因为协方差矩阵是对称矩阵，因此特征向量的是正交的，而lda从类别矩阵与类内方差考虑，不是对称阵，因此不一定是正交的；
e、lda用于分类降维，而pca均可用；
f、lda需要保证类内方差散布矩阵可逆；

5. t-SNE

从原理到代码，超详细介绍： 从SNE到t-SNE再到LargeVis.

二、分析代码

如何绘制PCA PCoA和NMDS? 下面是一段以PCA为例的R语言绘图代码，使用数据及绘图展示。

2D PCA

使用的数据：

1. 要绘图的矩阵文件 test.txt, 我这个是一个生物表达量数据。
   
2. 分组文件
   
   Samples一列脚本中没有用到，只要用到后两列，即指名样本分组情况以便于绘图渲染不同的颜色。

##for 2D and 3D PCA  Plot

library(ggplot2)
library(psych)
library(scatterplot3d)
##you need to change the work path
norm <- read.delim('./test.txt',sep='\t',header = T,check.names = F)
group_data <- read.delim(list.files(pattern = '.tsv'))
Group <- group_data$Z
Samples <- group_data$S
data <- norm[,-1]
row.names(data) <- norm[,1]
group_num <- length(names(summary(Group)))
sample_num <- length(names(summary(Samples)))

##start PCA calculation
after_t <- t(data)
pca  <- prcomp(after_t,cor=T,center=T,scale=T)
pca_percent <- summary(pca)
PC1_percent <- paste(pca_percent$importance[2,1]*100,'% variance')
PC2_percent <- paste(pca_percent$importance[2,2]*100,'% variance')
PC3_percent <- paste(pca_percent$importance[2,3]*100,'% variance')

##colors
colorss <- c('#003399','red','darkgreen','purple','deeppink3','firebrick2','#FF9900','#666600','#3333CC','#CC0033',
             '#FF66CC','#9966FF','#336666','#006600','#CC0066','#996600','#3366CC','#CC3300','#CCCC66','#990033')

#2D PCA Plot
a <- pca$x[,c(1,2)]
a<-as.data.frame(a)
a <-cbind(Group,a)
x <-a$PC1
y <-a$PC2

if(sample_num/group_num !=1){
     
qplot(x,y,type="n",
  xlab=paste("PC1:",PC1_percent),
  ylab=paste("PC2:",PC2_percent),color = Group)+
  stat_ellipse(lwd = 1,geom="path",lty = 2)+
  labs(title = '2D PCA Plot')+
  theme_bw()+
  theme(plot.title = element_text(hjust = 0.5))+
  theme(panel.grid = element_blank(), panel.background = element_rect(colour = "black", size = 1, fill = NA)) +
  theme(text = element_text(size = 15, family = "ArialMT"))+
  scale_y_continuous(limits = c(min(y) * 1.3, max(y) * 1.3)) +
  scale_x_continuous(limits = c(min(x) * 1.3, max(x) * 1.3)) +
  geom_point(size = 4) +
  #Adjust the vjust if lables of points not inside the fig
  geom_text(aes(label = group_data$S), size = 4,vjust = -1)+
  scale_color_manual(values= colorss[1:group_num])+
  scale_fill_manual(values= colorss[1:group_num])+
  geom_vline(xintercept = 0, linetype = 4, color = "grey") +
  geom_hline(yintercept = 0, linetype = 4, color = "grey") +
  coord_equal()
  ggsave("2D PCA Plot.png", height = 8, width = 8)
  }else{
     
  qplot(x,y,type="n",
        xlab=paste("PC1:",PC1_percent),
        ylab=paste("PC2:",PC2_percent),color = Samples)+
    stat_ellipse(lwd = 1,geom="path",lty = 2)+
    labs(title = '2D PCA Plot')+
    theme_bw()+
    theme(plot.title = element_text(hjust = 0.5))+
    theme(panel.grid = element_blank(), panel.background = element_rect(colour = "black", size = 1, fill = NA)) +
    theme(text = element_text(size = 15, family = "ArialMT"))+
    scale_y_continuous(limits = c(min(y) * 1.3, max(y) * 1.3)) +
    scale_x_continuous(limits = c(min(x) * 1.3, max(x) * 1.3)) +
    geom_point(size = 4) +
    #Adjust the vjust if lables of points not inside the fig
    geom_text(aes(label = group_data$S), size = 4,vjust = -1)+
    scale_color_manual(values= colorss[1:group_num])+
    scale_fill_manual(values= colorss[1:group_num])+
    geom_vline(xintercept = 0, linetype = 4, color = "grey") +
    geom_hline(yintercept = 0, linetype = 4, color = "grey") +
    coord_equal()
  ggsave("2D PCA Plot.png", height = 8, width = 8)
}

#3D Plot

z <-a$PC3
all_col <- factor(Group,levels= colorss[1:group_num])
png("3D PCA Plot-2.png",width = 900*3,height = 800*3,res = 90*3)
if(sample_num/group_num ==1){
     
  plot3d <- with(a,scatterplot3d(x, y, z, xlab = paste("PC1:",PC1_percent),
                                    ylab = paste("PC2:",PC2_percent), 
                                    zlab = paste("PC3:",PC3_percent), 
                                    main = "3D PCA Plot",color = colorss[1:group_num],
                                    pch = 16, label.tick.marks = TRUE, type = 'h', 
                                    angle = 45),mar = c(5.1,4.1,4.1,8.1))
}else{
     
  num <- vector()
  for (i in levels(Group)){
     
  num_1<-length(Group[Group==i])
  num=append(num,num_1)
}
  plot3d <- with(a,scatterplot3d(x, y, z, xlab = paste("PC1:",PC1_percent),
                                 ylab = paste("PC2:",PC2_percent), 
                                 zlab = paste("PC3:",PC3_percent), 
                                 main = "3D PCA Plot",color = rep(colorss[1:group_num],num),
                                 pch = 16, label.tick.marks = TRUE, type = 'h', 
                                 angle = 45),mar = c(5.1,4.1,4.1,8.1))
}
Position <- plot3d$xyz.convert(x, y, z)
text((Position$x)+0.15, (Position$y)+0.15, labels = Samples, cex = 0.8, 
     col = rep(colorss[1:group_num],num))

legend('topleft', pch = 16,xjust = 0.5, yjust = 0, legend = levels(Group), 
       cex = rel(1.2),col = colorss[1:group_num])
dev.off()

绘图展示：

2D 绘图结果，美美哒
3D 绘图效果，是美的哦

说明：PCA PCoA NMDS 的主要区别在于他们所所用的矩阵类型不同，具体的差别在上面已经介绍过了哦。三者均可以使用prcomp这个函数来计算主成分，即脚本可通用。

嘤嘤嘤，LDA的绘图以后再追加。