R语言mgcv包时间序列分析在空气污染与健康领域的应用(1)
在空气污染与健康研究领域,经常需要用时间序列方法将随时间变化的污染物暴露资料和随时间变化的事件发生数资料联系起来,分析人群健康结局与暴露水平之间的关系. 时间序列分析是根据系统观测得到的时间序列数据,通过曲线拟合和参数估计来建立数学模型的理论和方法。在空气污染健康效应研究中,通常采用泊松回归模型来估计每日污染物浓度变化与死亡人数、就诊人数等健康结局指标之间的关系。目前,国际上通常使用广义线 性模型 ( generalized linear models,GLM)与广义相加模型(generalized additive model,GAM)来实现泊松回归过程。
今天我们使用美国芝加哥1987年至 2000年大气污染与死亡数据做实例分析(公众号回复:芝加哥可以获得数据),我们先导入需要的R包和数据看看
library(mgcv)
library(splines)
library(tsModel)
bc<-read.csv("E:/r/test/chicago.csv",sep=',',header=TRUE)
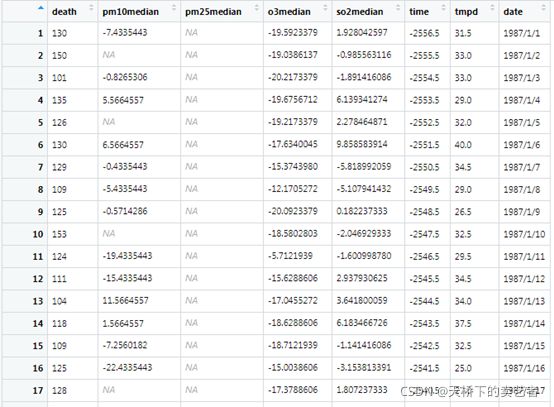
我们先来看看数据的构成,death:total deaths (per day),pm10median:大气污染物pm10的中位数值,pm25median:大气污染物pm25中值颗粒 < 2.5 mg/m3(更危险)(我怀疑就是我们通常说的PM2.5),o3median:二氧化硫的中位数值,time:天数,这里就是我们的时间,tmpd:华氏温度,最后一个date:这个数据本来是没有的,因为时间数据使用的是天数,不是我们的标准日期格式,我自己转换成日期格式,转换过程很简单,1987年至 2000年,我们取中间的年份进行转换,一行代码就可以了,有兴趣的可以自己试试
bc$date<-as.Date(bc$time,origin = "1994-01-01")##本行代码是进行数据转换,不是必要的代码
转成日期格式
bc$date1<-as.Date(bc$date, "%Y/%m/%d")
整理好生成数据后,我们就可以开始分析了
假设我们想知道气污染物pm10的浓度与死亡人数的关系,在评估空气污染与健康效应指标的关系时,由于对于总人口来说,每日死亡数、发病数是小概率事件,作为一种时间序列资料,其实际分布近似泊松分布,因此自变量和因变量之间的联接函数通常选取对数函数来进行分析。
我们先对指标pm10取平均移动值
bc$pm10lag01<-runMean(bc$pm10median,0:1)###产生 pm10lag01变量,赋值为过去两天大气PM10浓度的移动均值
建立模型
fit1<-glm(death~pm10lag01+ns(tmpd,3)+ns(o3median,3)+ns(date1,7*14),family = quasipoisson(),
data=bc) #GLM 模型拟合
summary(fit1)
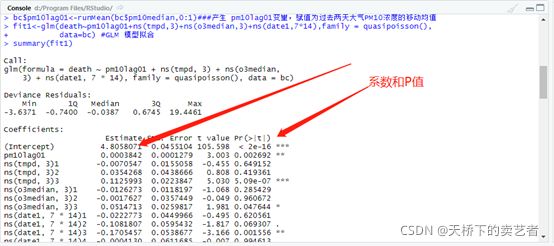
如图所示,P小于0.05,有统计学意义。我们还可以提取系数进行分析
b<-summary(fit1)$coeff[2,1]#提取系数
se<-summary(fit1)$coeff[2,2]#提取标准误
ER<-(exp(b*10)-1)*100 ####计算 PM 10每升高 10μg /m 3 ,死亡的超额危险度ER
ERlp<-(exp((b-1.96*se)* 10)-1)*100 #计算95%CI
ERup<-(exp((b+1.96*se)* 10)-1)*100 #计算95%CI
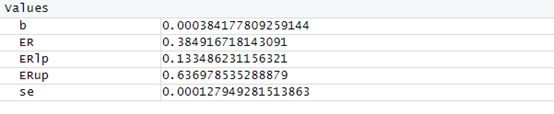
上述命令通过提取 fit3 模型配合结果中的回归系数与标准误,可计算出 PM 10 浓度每升高 10μg /m 3,人群总死亡增加的百分比及其 95% CI,即为 0. 34%(95%CI:0. 13% ~ 63%)
下面我们继续使用广义可加模型分析,这里时间单位不能使用date了,分析不了,要使用time,S( )表示平滑函数,常采用惩罚样条方法进行参数的平滑;k 等于 df + 1。此处温度、相对湿度 k 值均为4时间变量的k值取7/年 ×14 年+1。
fit2<-gam(death~pm10lag01+s(tmpd,k=4)+s(o3median,k=4)+s(time,k=7*14+1),family=quasipoisson(),
data=bc)#GAM 模型拟合
summary(fit2)
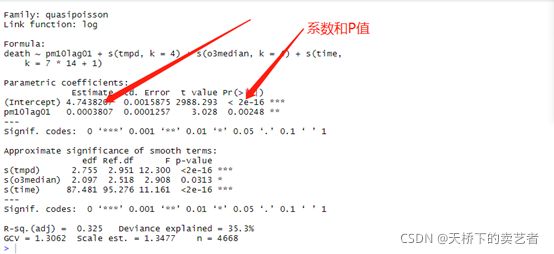
可以看到和GLM模型分析的差不多,后续分析差不多,就不进一步演示了,还可以进一步绘图;
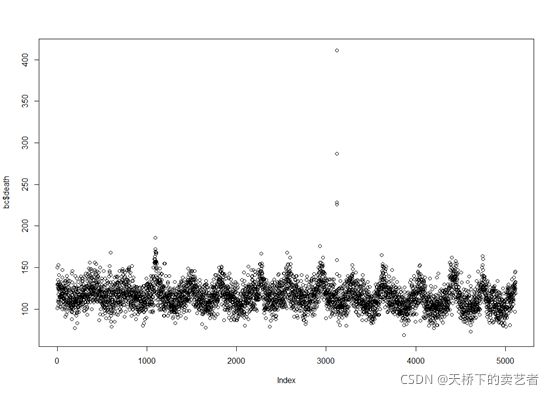
绘制时间序列图,以死亡人数为例
plot(bc$death)
acf(resid(fit1)) #绘制残差自相关图,以 fit1模型为例
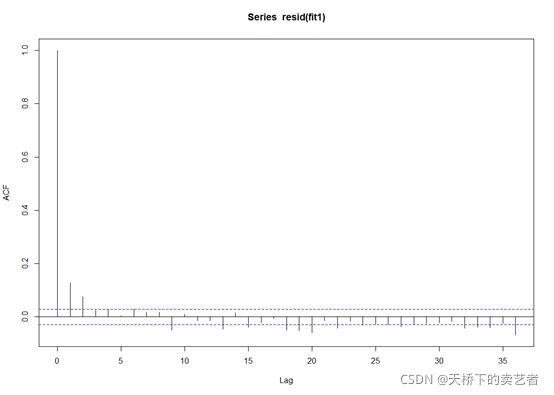
绘制偏自相关图,以 fit1模型为例

绘制模型暴露-反应关系图(污染物浓度和死亡率关系图)
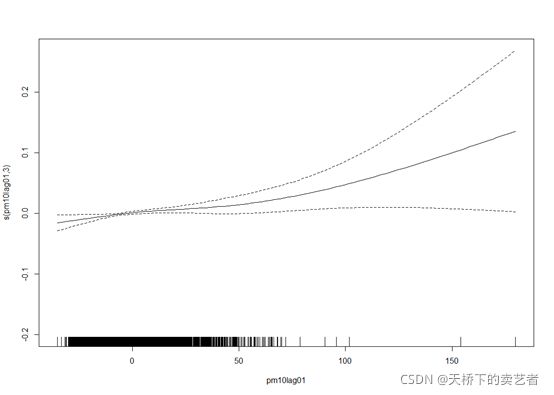
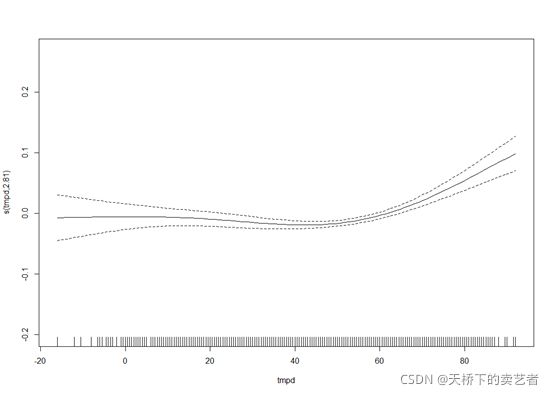

如图所示,随着pm10浓度增加,患者死亡率增加。
参考文献
- mgcv包解释文件
- tsModel包解释文件
- 杨敏娟, 潘小川. 北京市大气污染与居民心脑血管疾病死亡的时间序列分析[J]. 环境与健康杂志, 2008(4):4.
- 邓建明, 秦伯强, 王博雯. 广义可加模型在R中的快捷实现及蓝藻水华预测分析中的应用[J]. 生态学杂志, 2015, 34(3):8.
- 向伟. 广义可加模型在出生缺陷影响因素分析中的应用及R语言实现过程[J]. 中国妇幼保健, 2014, 29(29):5.
- 张云权, 朱耀辉, 李存禄,等. 广义相加模型在R软件中的实现[J]. 中国卫生统计, 2015, 32(6):3.
- 殷文军, 彭晓武, 宋世震,等. 广州市空气污染与城区居民心脑血管疾病死亡的时间序列分析[J]. 环境与健康杂志, 2012, 29(6):6.
- 路凤, 李亚伟, 李成橙,等. 时间序列分析在空气污染与健康领域的应用及其R软件实现[J]. 中国卫生统计, 2018, 35(4):4.
更多精彩文章请关注公众号:零基础说科研