目录
openGauss数据库SQL引擎
一.SQL引擎概览
二.SQL解析
三.查询优化
Ⅰ.查询重写
Ⅱ.路径搜索openGauss数据库执行器技术
openGauss存储技术
openGauss事务机制
openGauss数据库安全
openGauss数据库SQL引擎
三、查询优化
Ⅱ、路径搜索
优化器最核心的问题是针对某个SQL语句获得其最优解的问题,这个过程通常需要枚举SQL语句对应的解空间,也就是枚举不同的候选的执行路径,这些执行路径互相等价,但是执行效率不同,这对解空间中的这些执行路径计算它们的执行代价,最终可以获得一个最优的执行路径。依据候选执行路径的搜索方法的不同,将优化器的结构划分为如下几种模式:
§ 自底向上模式:如图5所示,自底向上的模式会对逻辑执行计划进行拆解,先建立对表的扫描算子,然后由扫描算子构成连接算子,最终堆成一个物理执行计划,在这个过程中,由于物理扫描算子和物理连接算子有多种可能,因此会生成多个物理执行路径,优化器会根据各个执行路径的估算代价选择出代价最低的执行计划,然后转交由执行器负责执行。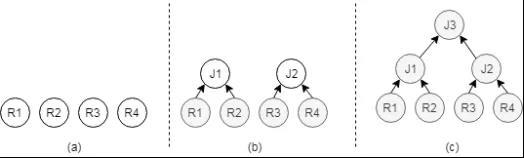
图5 自底向上模式
§ 自顶向下模式:该模式总体是运用面向对象思路,将优化器核心功能对象化,在词法分析、语法分析、语义分析后生成逻辑计划。基于此逻辑计划,应用对象化的优化规则,产生多个待选的逻辑计划,通过采用自顶向下的方法遍历逻辑计划,结合动态规划、代价估算和分支限界技术,获得最优的执行路径,如图6所示。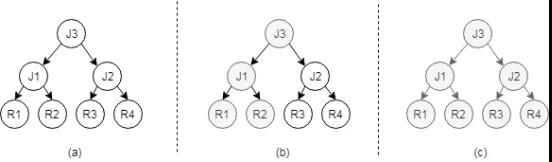
图6 自顶向下模式
§ 随机搜索模式:无论是自底向上模式还是自顶下模式,在参与连接的表的数量比较多的情况下,都会出现枚举时间过长的问题,一些优化器在表比较多的情况下通过一些随机枚举的方法对路径进行搜索,尝试在随机的解空间中获得次优的执行计划。
目前Oracle、MySQL、PostgreSQL等数据库的优化器采用的是自底向上模式,SQL Server以及开源的Calcite、ORCA则采用了自顶向下的模式,其中Calcite以良好的扩展性被广泛应用到其他开源项目里包括Apache Storm、Apache Flink、Apache Kylin、Apache Drill、SQL- Gremlin等项目。openGauss采用的是自底向上模式和随机搜索模式相结合的方式。
无论是自顶向下的搜索模式还是自底向上的搜索模式,搜索的过程也都是一个从逻辑执行计划想物理执行计划转变的过程,例如针对每个表可以有不同的扫描算子,而逻辑连接算子也可以转换为多种不同的物理连接算子,下面介绍一下具体的物理算子。
- 单表扫描路径搜索
GausssDB采用的是自底向上的路径搜索方法,因此路径生成总是从单表访问路径开始,对于单表访问路径,一般有两种:
§ 全表扫描:对表中的数据逐个访问。
§ 索引扫描:借助索引来访问表中的数据,通常需要结合谓词一起使用。
优化器首先根据表的数据量、过滤条件、可用的索引结合代价模型来估算各种不同扫描路径的代价。
例如:给定表定义CREATE TABLE t1(c1 int);如果表中数据为1,2,3…100000000连续的整型值并且在c1列上有B+树索引,那么对于SELECT * FROM t1 WHERE 从c1=1来说,只要读取1个索引页面和1个表页面就可以获取到数据。然而对于全表扫描,需要读取1亿条数据才能获取同样的结果。在这种情况下索引扫描的路径胜出。
索引扫描并不是在所有情况下都优于全表扫描,它们的优劣取决于过滤条件能够多滤掉多少数据,通常数据库管理系统会采用B+树来建立索引,如果在选择率比较高的情况下,B+树索引会带来大量的随机IO,这会降低索引扫描算子的访问效率。比如SELECT * FROM t1 WHERE c1>0;这条语句,索引扫描需要访问索引中的全部数据和表中的全部数据,并且带来巨量的随机IO,而全表扫描只需要顺序的访问表中的全部数据,因此在这种情况下,全表扫描的代价更低。
- 多表连接路径搜索
多表路径生成的难点主要在于如何枚举所有的表连接顺序(Join Reorder)和连接算法(Join Algorithm)。
假设有两个表t1和t2做JOIN操作,根据关系代数中的交换律原则,可以枚举的连接顺序有t1 × t2和t2 × t1两种,JOIN的物理连接算子有Hash Join、Nested Loop Join、Merge Join三种类型。这样一来,可供选择的路径有6种之多。这个数量随着表的增多会呈指数级增长,因此高效的搜索算法显得至关重要。
openGauss通常采用自底向上的路径搜索方法,首先生成了每个表的扫描路径,这些扫描路径在执行计划的最底层(第一层),在第二层开始考虑两表连接的最优路径,即枚举计算出每两表连接的可能性,在第三层考虑三表连接的最优路径,即枚举计算出三表连接的可能性,直到最顶层为止生成全局最优的执行计划。
假设有4个表做JOIN操作,它们的的连接路径生成过程如下:
§ 单表最优路径:依次生成{1},{2},{3},{4}单表的最优路径。
§ 二表最优路径:依次生成{1 2},{1 3},{1 4},{2 3},{2 4},{3 4}的最优路径。
§ 三表最优路径:依次生成{1 2 3},{1 2 4},{2 3 4},{1 3 4}的最优路径。
§ 四表最优路径:生成{1 2 3 4}的最优路径即为最终路径。
多表路径问题核心为Join Order,这是NP(Nondeterministic Polynomially,非确定性多项式)类问题,在多个关系连接中找出最优路径,比较常用的算法是基于代价的动态规划算法,随着关联表个数的增多,会发生表搜索空间膨胀的问题,进而影响优化器路径选择的效率,可以采用基于代价的遗传算法等随机搜索算法来解决。
另外为了防止搜索空间过大,openGauss采用了三种剪枝策略:
§ 尽可能先考虑有连接条件的路径,尽量推迟笛卡尔积。
§ 在搜索的过程中基于代价估算对执行路径采用LowBound剪枝,放弃一些代价较高的执行路径。
§ 保留具有特殊物理属性的执行路径,例如有些执行路径的结果具有有序性的特点,这些执行路径可能在后序的优化过程中避免再次排序。
- 分布式路径搜索
openGauss优化引擎可以生成高效的分布式路径。在分布式架构下,同一个表的数据会分布到不同的DN上,创建表的时候可以选择将数据在每个表上做Hash分布或者Random分布,为了正确执行两表连接操作,可能需要将两个表的数据做重新分布才能得到正确的连接结果,因此openGauss的分布式执行计划中增加了对数据进行重分布的两个算子:
§ Redistribute:将一个表的数据按照执行的Hash值在所有的DN上做重分布。
§ Broadcast:通过广播的方式重新分布一个表的数据,保证广播之后每个DN上都有这个表的数据的一份副本。
分布式路径生成时,会考虑两表以及连接条件上的数据是否处于同一个数据节点,如果不是,那么会添加相应的数据分发算子。例如:
CREATE TABLE t1(c1 int, c2 int) DISTRIBUTE BY hash(c1);
CREATE TABLE t2(c1 int, c2 int) DISTRIBUTE BY hash(c2);
SELECT * FROM t1 JOIN t2 ON t1.c1=t2.c1;
其中表t1采用的是Hash分布方法,其分布键为c1列,表t2采用的也是Hash分布方法,其分布键为c2列,由于SELECT查询中选择条件是在t1.c1和t2.c2上做连接操作,这两个列的分布不同,因此做连接之前需要添加数据重分布来确保连接的数据在同一数据节点上。那么有如下几种可供选择的路径如图7所示。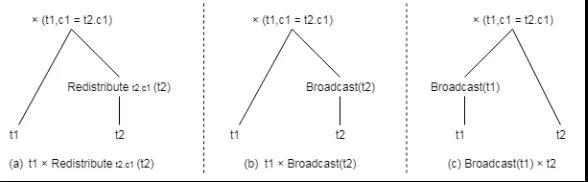
图7 分布式计划示例
根据分发算子所需要处理的数据量以及网络通信所带来的消耗,可以计算这些路径的代价,openGauss优化引擎会根据代价从中选出最优的路径。
- 利用物理属性优化
关系的本身可以视为一个集合或者包,这种数据结构对数据的分布没有设定,为了提升计算的性能,我们需要借助一些数据结构或算法来对数据的分布做一些预处理,这些预处理方法或者利用了物理执行路径的物理属性(例如有序性),或者为物理执行路径创建物理属性,总之这些属性经常会在查询优化中发挥巨大的作用。
1) B+树
如果要查询一个表中的数据,最简单的办法自然是将表中的数据全部遍历一遍,但是随着当前数据量的越来越大,遍历表中数据的代价也越来越高,而B+树就成了我们高效的查询数据的有力武器。
1970年,R.Bayer和E.mccreight提出了一种适用于外查找的树,它是一种平衡的多叉树,称为B树,B树就是在表的数据上建立一个“目录”,类似于书籍中的目录,这样就能快速的定位到要查询的数据。
B+树作为一种数据结构和查询优化器本身没有直接的关系,但是数据库管理系统通常会建立基于B+树的索引,而在查询优化的过程中,可以通过索引扫描、位图扫描的方法提高查询效率,这都会涉及到这种B+树类型的索引的使用。
2) Hash表
Hash表也是一种对数据进行预处理的方法,openGauss数据库在多个地方使用了Hash表或借用了Hash表的思想来提升查询效率:
§ 借用Hash可以实现分组操作,因为Hash表天然就有对数据分类的功能。
§ 借用Hash可以建立Hash索引,这种索引适用于等值的约束条件。
§ 物理连接路径中Hash Join是非常重要的一条路径。
3) 排序
排序也是一种对数据进行预处理的方法,它主要用在以下几个方面:
§ 借用排序可以实现分组操作,因为经过排序之后,相同的数据都聚集在一起,因此它可以用来实现分组。
§ B树索引的建立需要借助排序来实现。
§ 物理连接路径Merge Join路径需要借助排序实现。
§ SQL语言中的Order By操作需要借助排序实现。
在数据量比较小时,数据可以全部加载到内存,这时候使用内排序就能完成排序的工作,而当数据量比较大时,则需要使用外排序才能完成排序的工作,因此在计算排序的代价时需要根据数据量的大小以及可使用的内存的大小来决定排序的代价。
4) 物化
物化就是将扫描操作或者连接操作的结果保存起来,如果在中间结果比较大的情况下可能需要将结果写入外存,这会产生IO代价,因此这种保存是有代价的。
物化的优点是如果内表可以一次读取多次使用,那么就可以将这个中间结果保存下来多次利用,例如有t1表和t2表做连接,如果t2表作为内表经过扫描之后,只有5%的数据作为中间结果,其他95%的数据都被过滤掉了,那么就可以考虑将这5%的数据物化起来,这样t1表的每条元组就只和这5%的数据进行连接就可以了。
中间结果是否物化主要取决于代价计算的模型,通常物理优化生成物理路径时对物化和不物化两条路径都会计算代价,最终选择代价较低的一个。
未完待续......