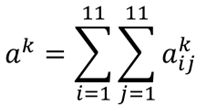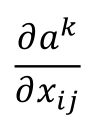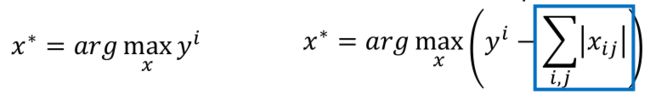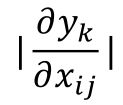【机器学习基础】卷积神经网络（CNN）基础

最近几天陆续补充了一些“线性回归”部分内容，这节继续机器学习基础部分，这节主要对CNN的基础进行整理，仅限于基础原理的了解，更复杂的内容和实践放在以后再进行总结。

---

卷积神经网络的基本原理 

　　前面对全连接神经网络和深度学习进行了简要的介绍，这一节主要对卷积神经网络的基本原理进行学习和总结。

　　所谓卷积，就是通过一种数学变换的方式来对特征进行提取，通常用于图片识别中。

　　既然全连接的神经网络可以用于图片识别，那么为什么还要用卷积神经网络呢？

0.使用卷积神经网络的理由

（1）首先来看下面一张图片：

　　在这个图片当中，鸟嘴是一个很明显的特征，当我们做图像识别时，当识别到有“鸟嘴”这样的特征时，可以具有很高的确定性认为图片是一个鸟类。

　　那么，在提取特征的过程中，有时就没有必要去看完整张图片，只需要一小部分就能识别出一定具有代表的特征。

　　因此，使用卷积就可以使某一个特定的神经元（在这里，这个神经元可能就是用来识别“鸟嘴”的）仅仅处理带有该特征的部分图片就可以了，而不必去看整张图片。

 　　那么这样就会使得这个神经元具有更少的参数（因为不用再跟图片的每一维输入都连接起来）。

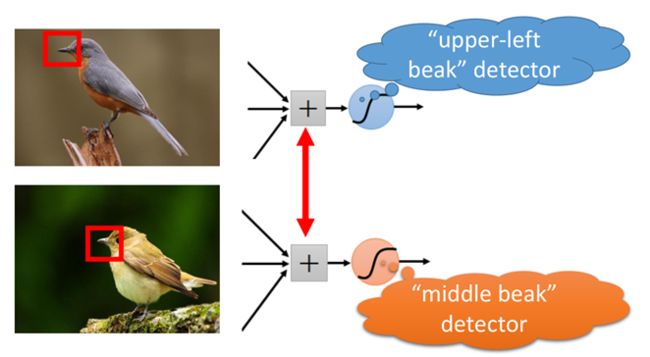
（2）再来看下面一组图片：

 上面两张图片都是鸟类，而不同的是，两只鸟的“鸟嘴”的位置不同，但在普通的神经网络中，需要有两个神经元，一个去识别左上角的“鸟嘴”，另一个去识别中间的“鸟嘴”：

　　但其实这两个“鸟嘴”的形状是一样的，这样相当于上面两个神经元是在做同一件事情。

　　而在卷积神经网络中，这两个神经元可以共用一套参数，用来做同一件事情。

（3）对样本进行子采样，往往不会影响图片的识别。

　　如下面一张图：

　　假设把一张图片当做一个矩阵的话，取矩阵的奇数行和奇数列，可看做是对图片的一种缩放，而这种缩放往往不会影响识别效果。

　　卷积神经网络中就可以对图片进行缩放，是图片变小，从而减少模型的参数。

1.卷积神经网络的基本结构

　　卷积神经网络的基本结构如图所示：

　　从右到左，输入一张图片→卷积层→max pooling（池化层）→卷积层→max pooling（池化层）→......→展开→全连接神经网络→输出。

　　中间的卷积层和池化层可以重复多次。后面会一一介绍每一层是如何工作的。

　　对于第0部分的三个功能：

　　（1）某个神经元只需侦测某一部分的图片，来识别某种特征这个工作是在卷积层内完成的。

　　（2）具有相同功能的神经元共用一套参数，这个工作也是在卷积层内完成的。

　　（3）通过缩小图片，来减少模型的参数，这个工作是在池化层中完成的。

　　稍后会解释上面三个部分是如何进行的。

1.1.卷积层的工作原理

　　假设有一张6*6的黑白图片，如图所示：

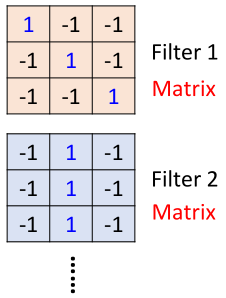
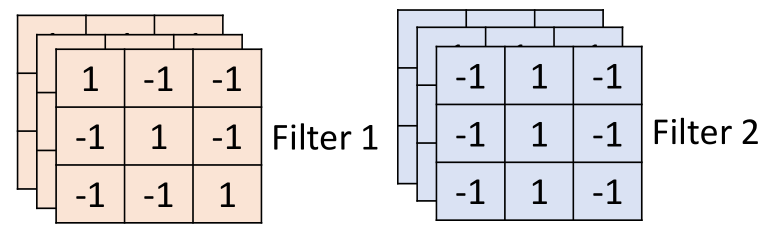
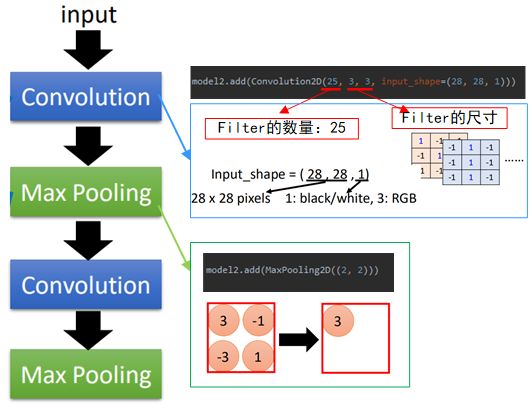
　　首先图片经过卷积层，卷积层有一组filter，每个filter用来抓取图片中的某一种特征，如图所示：

　　假设filter是3*3的矩阵，每个filter有9个参数，而这些参数就是通过训练学习得到的，这里假设我们已经学习得到了上面一组参数的值。

　　因此也就说明了问题（1）中，每一个filter只侦测图片中的很小一部分数据。

　　那么每个filter是如何去抓取特征的呢？也就是（1）中使某一个神经元只侦测一部分图片就能提取某一种特征的问题。

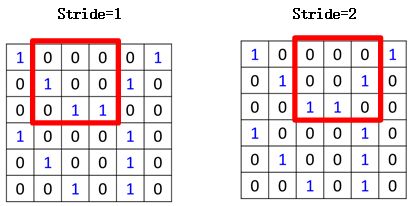
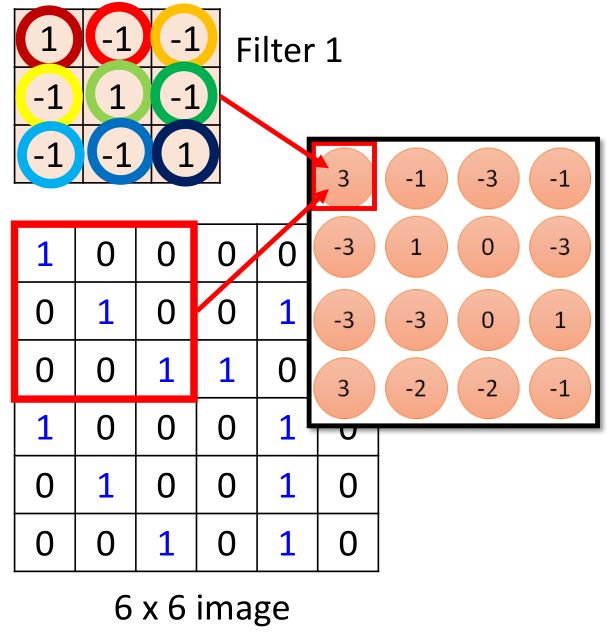
　　首先看filter1，filter大小为3*3，那么相当于这个filter1依次从左到右去覆盖整张图片，然后与覆盖区域做内积，如图所示：

　　首先从左上角开始，覆盖图片左上角3*3的区域，计算结果得到3，然后向右移动，这里移动的步长称之为stride，当stride为1时，即一次移动一格，为2时，一次移动两格，如图所示：

　　移动之后再次用图片被覆盖的区域与filter做内积，得到第二个值：

　　依次进行移动和计算，当移到最右边尽头时，则从下一行开始继续移动，最终得到如图所示矩阵：

　　通过观察这个filter1可以看出，filter1的对角矩阵全为1，其他为-1，那么对于图片中对角为1的部分，与filter1做内积后的值就会很大（例子中等于3），其他的则会很小。

　　因此filter1是一种用于侦测对角都为1的图片这种属性，在图片中可以看到，坐上角和右下角都具有这种特征。

　　所以这也就说明了（2）中的问题，一个filter的一组参数，可以侦测到图片中两个位置的相同属性。

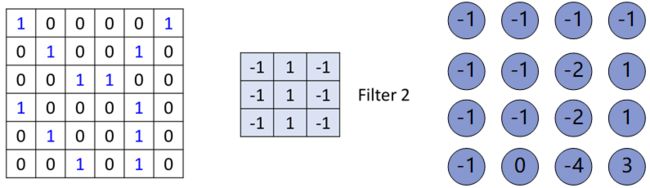
　　接下来是第二个filter，filter2，那么filter2与图片的计算方式一模一样，如图所示：

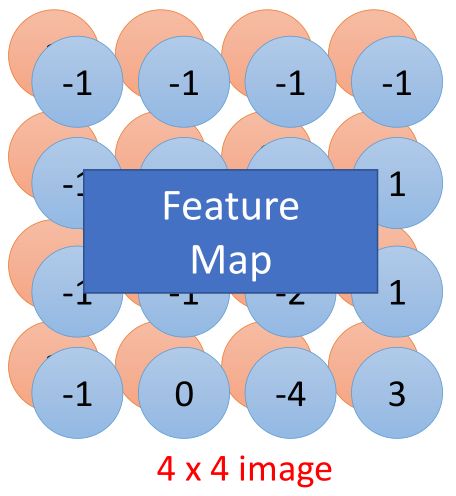
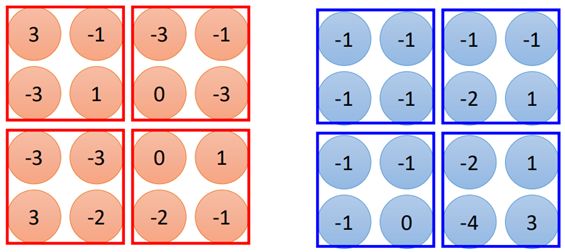
　　其他的filter也是如此，依次计算，然后把每个filter处理结果放在一起，如图所示：

　　那么相当于一个红色方框现在是由2个值来描述的，最终得到的是2个4*4的图片，称之为“feature map”。

　　上面是对于一张黑白的图片进行一次卷积（convolution）的过程，那么对于彩色的图片是怎样处理的呢？

　　彩色图片通常是由“RGB”组成，分别表示红色、绿色和蓝色，那么就相当于有三个部分的组成，如图所示：

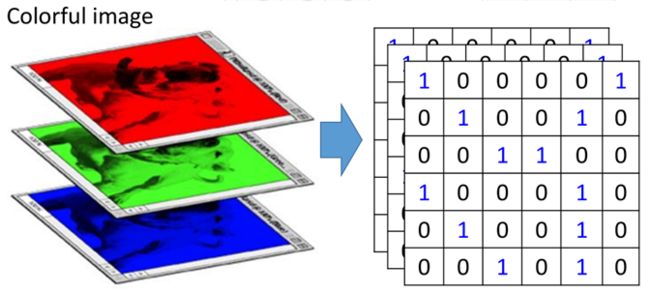　　这三个层称之为“通道”（channel），那么利用卷积处理这种图片时，filter也应该是三层，即3*3*3的，是带有深度的，长下面这个样子：

　　相当于每个filter具有27个参数。

卷积与全连接网络的关系

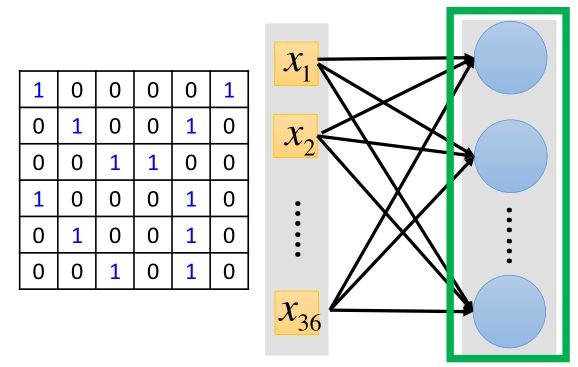
　　其实卷积就是一种特殊形式的全连接网络，还是假设是上面那张6*6的图片，如下是全连接的网络结构：

　　把图片进行拉直展开，但在卷积中，这个网络有些连接的地方被切断了，只有一部分输入与神经元相连接。下面进行解释：

　　正如上面的卷积过程，如下是其中的一步，如图所示：

　　那么这个步骤我们可以想象成是这样子的：

　　左边把图片的36个数值拉直，然后，对于filter1所覆盖的区域为左上角，那么元素对应的位置为1、2、3、7、8、9、13、14、15。

　　然后这9个数值，依次经过各自的weight相乘再相加，得到第一个值3，这里的weight就是对应的filter中各个位置的值，图中weight线的颜色与filter中圆圈颜色一一对应。

　　到这里就很清楚的看出卷积与全连接之间的关系，相当于简化了全连接神经网络，从而使得参数量更少。

　　然后filter开始向右移动一格（stride=1，上面计算过程的第二个方框，元素依次为2、3、4、8、9、10、14、15、16）,与filter做inner product，得到结果-1，对应到全连接网络中如图所示：

　　依旧是每个元素的weight与输入输出连接，颜色对应的filter圆圈与weight的颜色一致。

　　从上面的图可以看出，两个神经元（3和-1）都是通过filter1作为weight与输入进行连接的，也就是说，这两个神经元是共用同一组参数，这样，在上面减少参数的基础上，使得模型的参数更少了。

　　上述过程就是卷积层的工作过程，主要用于图片中特征的抓取，完成第0节内容的前两个。

1.2池化层的工作原理

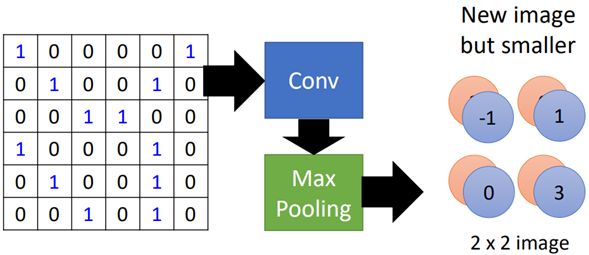
　　池化层的作用上面说了，就是为了图片的缩放，那么池化层是如何进行缩放的呢？

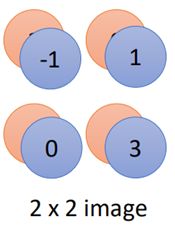
　　其实池化层的原理很简单，这里以max-pooling为例，经过卷积层之后的图片变为4*4大小的图片，有2个filter，也就是两张4*4的图片：

　　池化就是将上面得到的数据进行分组，如图所示：

　　如图示中的分组方法，这种分组方法可以是任意的，也可以三个一组等等，然后取每个组中的最大值：

　　那么原来4*4的图片经过maxpooling之后就缩小为2*2的图片了，当然这里也不一定非要取最大值，也可以取平均，或者又取平均又取最大值等。

　　那么上面的过程总结一下就可以用如下图进行概括：

 

　　这就是池化层的工作原理，比较简单。

1.3Flatten和全连接层

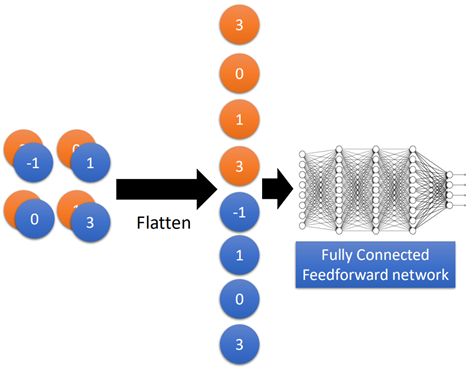
　　接下来就来到了flatten和全连接层了，flatten的作用就是把上面得到的两个2*2的image拉直展开，然后再丢进全连接网络中计算就可以了，这个跟前面全连接神经网络的方法一样，如图所示：

　　这里就不再详细赘述了。那么整个网络就是利用梯度下降的方法进行训练的，所有的参数被一起学习得到。

2.使用Keras对CNN的简单实现

　　这里还是使用keras对CNN的建模过程进行一个简单的实现，首先先来看一下keras分别添加卷积层和池化层的过程：

　　如图中所示，首先要导入Convolution2D（后来这个接口会改成Conv2D）和Maxpooling2D。

　　然后与之前神经网络中一样，不过是把“Dense”换成了上面两个方法，其中Convolution2D中，25表示filter的数量，3,3表示filter的尺寸，input_shape为输入图片的大小，28*28为图片大小，1表示黑白图片，3则表示彩图“RGB”；

　　Maxpooling2D中只有分组的形状，即2*2大小的。

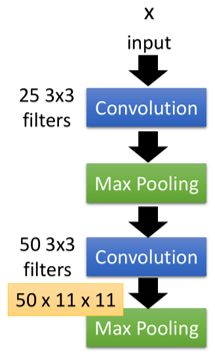
　　接下来就是根据设计的网络的形状，重复上面两个步骤，完成卷积和池化。如图所示：

　　图中黑色的方框为代码的实现内容，在keras1.0和2.0中可能有些差异；

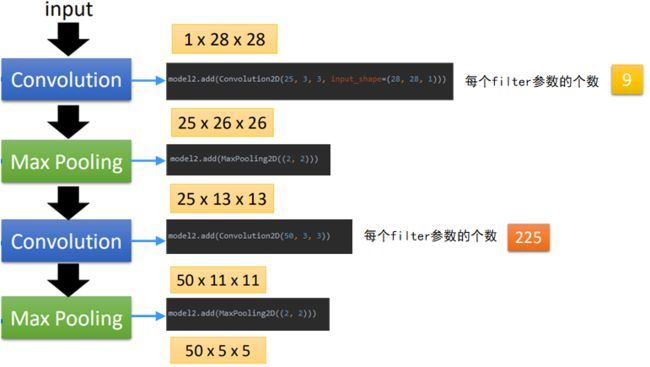
　　黄色的框中是输入和输出的尺寸大小，可以看到，输入为28*28的图片，经过25个3*3的filter组成的第一个卷积层之后，变成了25*26*26的尺寸；

　　然后经过第一个2*2的池化层，缩小后的输出尺寸大小为25*13*13；

　　然后经过第二个由50个3*3的filter之后，输出变为50*11*11；

　　之后经过第二个2*2的池化层后，缩小后的输出尺寸变为50*5*5（这里由于输入为基数，最后一格就忽略掉了）。

　　而在卷积层中，filter的参数数量是在变化的，在第一个卷积层的参数为3*3=9个，这个比较好理解；

　　而在第二个卷积层中，参数就变成了225个，这是因为上一层的输出为25*13*13大小的图片，这时是带有channel的（就相当于一开始输入为RGB时，通道数为3）当使用3*3的filter进行处理时，需要带有深度25，因此每个filter的参数数量为25*3*3=225。

　　然后就是经过Faltten和fully-connection了，这个与之前的神经网络一致：

　　然后就可以对模型进行训练了。这里要注意的是，这里的输入跟全连接有所不同，要把输入图片数据转化为（28,28,1）的格式。完整代码如下：

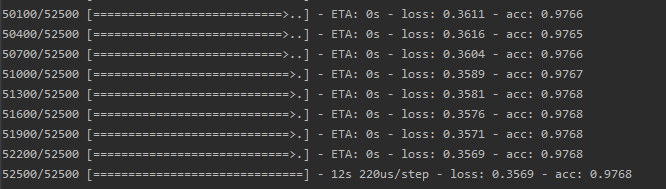
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import train_test_split
import numpy as np
from keras import Sequential
from keras.layers import Dense
from keras.layers import Activation
from keras.layers import Convolution2D, MaxPooling2D, Flatten

data_x, data_y = fetch_openml('mnist_784', version=1, return_X_y=True)

x = []
for i in range(len(data_x)):
    tmp = data_x.iloc[i, :].tolist()
    tmp = np.array(tmp).reshape((28, 28, 1))
    x.append(tmp)
x = np.array(x)

one_hot = OneHotEncoder()
data_y = one_hot.fit_transform(np.array(data_y).reshape(data_y.shape[0], 1)).toarray()
train_x, test_x, train_y, test_y = train_test_split(x, data_y)

model2 = Sequential()

model2.add(Convolution2D(25, 3, 3, input_shape=(28, 28, 1)))

model2.add(MaxPooling2D((2, 2)))

model2.add(Convolution2D(50, 3, 3))

model2.add(MaxPooling2D((2, 2)))

model2.add(Flatten())
model2.add(Dense(units=100))
model2.add(Activation('relu'))
model2.add(Dense(units=10))

model2.add(Activation('softmax'))

model2.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

model2.fit(train_x, train_y, batch_size=300, epochs=20)

最后的输出如下：

3.CNN都学到了啥？

　　通过CNN的原理我们大致知道，CNN的卷积是不断提取特征的过程，池化是对图片的缩放，那么究竟CNN学习到了什么呢？如下面一张图：

　　给机器一张图片，那么对人来说，这张图片是一双鞋，而对机器来说，它可能认为是是美洲狮，因为图中的鞋标有一只美洲狮。

　　因此，我们想要知道CNN究竟学习到了啥，下面介绍几种方法来查看CNN都在侦测什么特征的方法。

3.1 直接查看filter

　　前面我们说到，filter就是为了抓取某一种特征的，那么我们是不是可以看一下这些filter分别都是侦测什么样的特征的。

　　根据CNN的原理，随着网络越来越靠近输出层，那么这一层所学习到的东西就越来越抽象，不太容易观察。因此，我们选取第一个卷积层的filters来看一下。

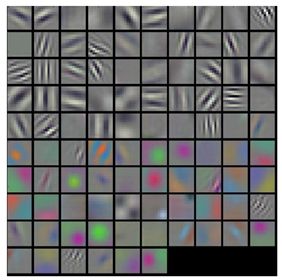
　　对于一个训练好的模型，将第一个卷积层的filters单独拿出来，并画出来，如图所示：

　　上面一共96个filter，每个filter的大小为11*11，从filter我们可以看出，上面几排的filter主要是侦测形状特征的，下面几排的filter主要是侦测色彩特征的。

　　我们也可以通过单独看一个filter，然后把图片依次输入的CNN中，看哪些图片经过这个filter后的输出（Activate）最大，如下图所示：

　　白色的框表示filter，这里白色的框看着很大，主要是因为这个filter比较靠后，也就是它所看到的是前面经过缩小后的输入，因此框就会变得很大。

　　第一排的图片中的框是一个filter1，可以看到，这个filter对于脸部的侦测比较强；

　　第二排的框是另一个filter2，可以看到filter2侦测的主要是洞状排列的特征；

　　第三排的filter3则是侦测红色的特征；

　　以此类推...

3.2 特征的可视化

　　这种方法是查看特征的，也就是说使用反卷积、反池化的方法，来可视化输入图像的激活特征。

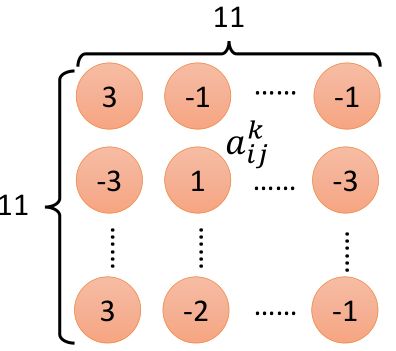
　　还用原理部分那个CNN结构的例子，如下图左边的结构：

                           

　　在第二个卷积层中，假设第k个filter，它与输入作用以后得到的结果如上图中右侧，每一个元素aij，然后把aij相加，即为ak，即：

　　那么现在我们想要通过输入x使得ak最大，也就是找一张图片x，使得ak的输出最大，即：

这里就要利用gradient ascent的方法去找这个最大值了，即求：

　　就相当于原先经过卷积、池化过程，现在要将x当做未知量，反过来求反池化、反卷积去求解出一个使得ak最大的x（注意这里x并不是真正的图片了，相当于是通过反池化和反卷积所得到的的带有一些特征的图像）；

　　具体原因就在于反池化和反卷积的求解过程，无法还原为原先的图片，这里暂不过多介绍如何反池化和反卷积的原理，后续再补充。

　　那么经过上面的步骤，还原得到的x的结果如图所示：

 　　一共50个filter，这里取前12个，每个图片的意思代表1个filter所还原得到的图片x，也就是说，比如第一张图片，将其作为input丢进上面那个网络后，其输出与第一个filter作用后得到的ak最大。

　　仔细观察一下上面的图，还是有一定的规律可循的。

　　同时我们也可以去查看fully-connection部分的神经元，原理跟上面一样，不过再求解释时又多了一层反向传播的过程，如图：

　　当然也可以去拿输出层的神经元，比如识别结果为0，输出层在第0维值就很大，然后一样根据上面的原理得到的结果如图：

　　会发现得到的结果什么也看不到，但是当把某张图片再次输入进网络之后，得到的确实是对应的结果。

　　这也就说明了深度学习很容易被欺骗，但从侧面也反映出了，深度学习确实学习到了某些特征，并非仅仅简单“记住”数据，也说明深度学习的“玄学”性，难以解释。

　　当然，在上面的求解过程中，我们可以适当加一些限制，比如正则化：

　　那么得到的结果如图：

　　发现结果稍微清晰了一些，有些能够看到一些笔画。

　　那么正则化的目的是在保证y越大越高的同时，也要使得xij（图片中的每一个pixel）越小越好，也就是说对于图片显示（白色的是笔画，黑色的是空白）时，尽可能使空白减少，能连的连起来。所以效果会好些。

3.3 微分

　　对于一张图片的识别，我们可以计算类别y对图像像素pixel的微分的值：

　　通过改变像素xij，来看这个像素对识别的影响是否重要，也就是说，当xij稍微做一下改变，对识别的结果影响有多大，用这样的方法可以得到如下的结果：

　　白色区域表示对识别影响较为重要的pixel，可以大概看到一些形状。那这样做有什么意义呢？

　　有时当我们从网上爬取图片进行建模后，发现对马的识别率很高，但对其他的识别一般，这是因为可能关于“马”的图片都包含“horse”字样的标签，机器真正识别到的是“horse”的标签，而并非知道马长什么样子。

　　同样的道理，我们可以通过盖住图片的一部分，去看看盖住的部分结果的影响有多大，比如：

　　图中灰色的区域是被盖住的，不断移动灰色的区域，看对结果的影响有多大，那么可以获取到下面一样的热力图：

　　图中颜色越浅表示对辨识的结果影响越大，越不能辨别出是什么，可以看到，第一张当盖住狗的脸的时候，很难分辨出狗；

　　第二张图片当盖住轮胎部分的时候，就很难辨别出轮胎；

　　第三张图片当盖住狗的身子的部分，就很难辨别出狗了。

　　更多有关CNN可视化的内容，可搜索一些有关博客进行学习：https://blog.csdn.net/xys430381_1/article/details/90413169

4.关于CNN一些有趣的应用

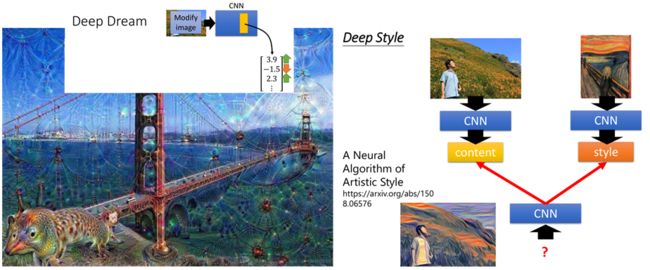
　　根据上面的理论，我们可以通过修改某个filter的参数，去还原出一张另类的图片，比较有趣的应用有deep dream和风格迁移，如下图（图片来源于网络）：

这里就暂时不具体介绍原理了，后面会找一些开源的项目去玩。

 

参考资料：台大李宏毅《机器学习-卷积神经网络》

---

 

上面是对CNN进行的一个初步的介绍，后面会对深度学习部分进行系统的学习和整理，这里主要是对原理有个初步的认识，因此很多都是概念性的东西，后续会进一步添加补充。