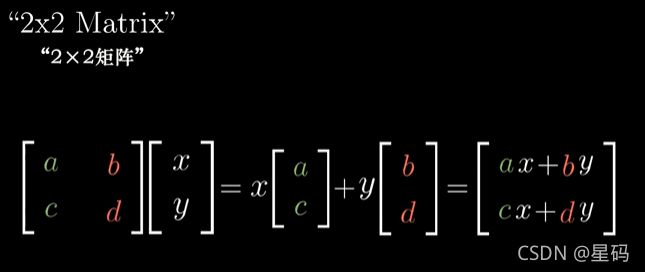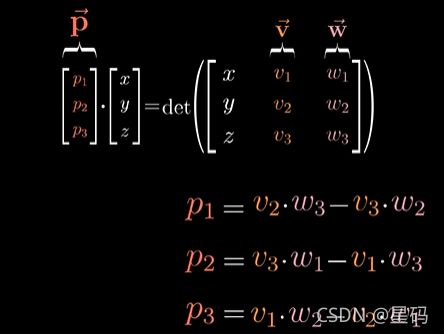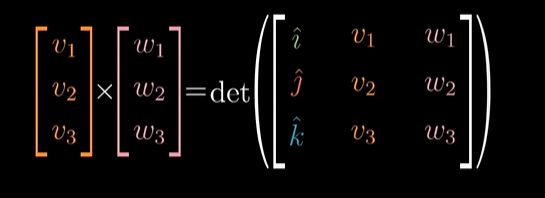线性代数的本质
线性代数的本质
- 一:矩阵与线性变换 - 矩阵:对空间的一种特定的变换
-
- 1. 知变换后基向量 i , j i,j i,j的坐标,利用变换前后的线性组合不变,得到变换后的 v v v的坐标
- 2. 定义矩阵列的含义:基向量变换后的坐标
- 3. 定义矩阵与向量的乘法:线性变换 作用于 给定的向量
- 二:矩阵与矩阵的乘法 - 线性变换复合
-
- 1. 两个矩阵相乘:就是两个线性变换的相继作用
- 2. 对两个矩阵相乘的过程的两种理解
- 3. 运算律
-
- 1. 矩阵相乘时,先后顺序会影响结果
- 2. 结合律(Associativity)
- 4. 行列式 - 测量变换对空间有多少拉伸或挤压
-
- 1. 从二维与三维理解行列式
- 2. 如何计算行列式
- 三:逆矩阵,列空间,零空间
-
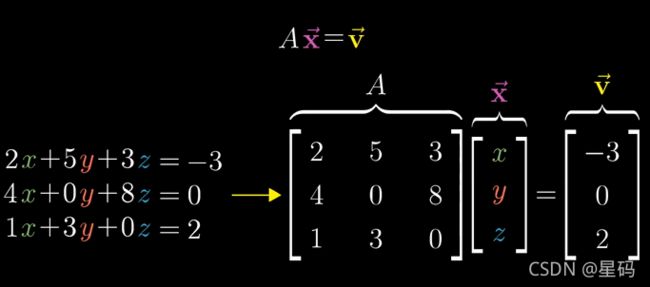
- 1. A x = v Ax=v Ax=v 求解 x x x时 --- 逆矩阵 与 行列式为0的理解
- 2. Rank - 秩:变换后空间的维度/列空间的维数
- 3. 列空间 --- 矩阵的列所张成的空间
- 4. 零空间 --- 变换后的向量 落在零向量上的 向量的集合
- 5. 综合 --- 从几何角度求解线性方程组:从逆矩阵,列空间,零空间
- 四:非方阵几何含义 --- 不同维度的映射
- 五:点积与其对偶性
-
- 1. 点积与其几何解释 --- 正交投影后长度相乘,正负与两个向量朝向有关
- 2. 对偶性(duality):点积 与 对应坐标相乘并相加 之间的联系
-
- 1. 线性变换简化成一个等价的直观特性
- 2. 向量 线性变换为数 与 映射矩阵对应向量 存在的关系:应用映射矩阵线性变换 和 与映射矩阵对应的向量(对偶向量)做点积 是一样的结果
- 3. 过程总结,对偶性,与点积含义
- 六:叉积
-
- 1. 叉积的介绍与计算 --- 两个向量围成平行四边形面积与长度同,方向遵循右手定则的一个向量
- 2. 叉积对偶性 --- 叉积所得向量几何意义是对偶向量
- 参考视频
以下讨论时:(如果之后有特殊情况会进行表明)
- 方程组都为线性方程组
- 且矩阵默认都为方阵 — 之后内容中,矩阵的每列都表示变换后基向量的坐标,设:矩阵有 a a a列说明变换前空间是 a a a维,而变换后的基向量坐标仍然需要在原始十字坐标系中表示(即变换后基向量用 a a a维表示),所以行与列应该相同
- 当然矩阵也有不为方阵(出现时会表明) — 这意味着变换经过变换后改变了维度,在第五章点积中体现的较多
一:矩阵与线性变换 - 矩阵:对空间的一种特定的变换
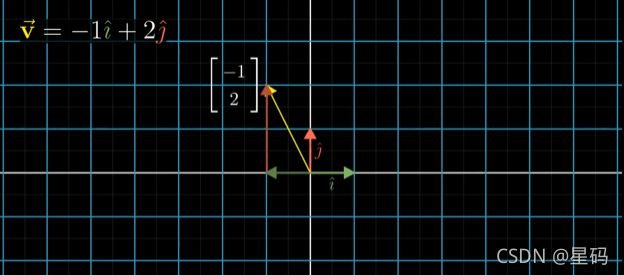
1. 知变换后基向量 i , j i,j i,j的坐标,利用变换前后的线性组合不变,得到变换后的 v v v的坐标
由图中根据变换后的三个向量的关系,可以得到:
如果向量v原来的坐标为(-1,2)
变换前向量 v 与 基向量 i 与 j 的线性组合为 v = − 1 i + 2 j v=-1i+2j v=−1i+2j (也就是将v的坐标看成线性组合,这有助于之后的理解)
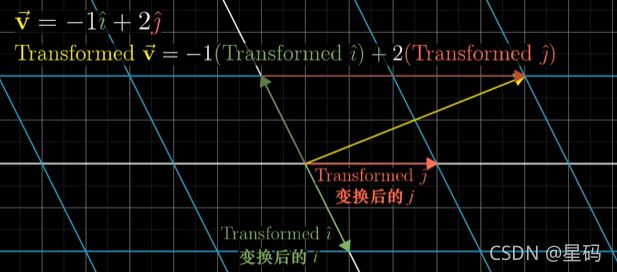
那么变换后的 v 也是变换后的 i 和 j 的同样的线性组合 T ( v ) = − 1 T ( i ) + 2 T ( j ) T(v)=-1T(i)+2T(j) T(v)=−1T(i)+2T(j) (由上图关系可得)

所以知道变换后的基向量 i , j i,j i,j的坐标,利用变换前 v , i , j v,i,j v,i,j之间的线性组合,可以得到变换后的 v v v的坐标(在图中可以看到,变换后的向量的坐标仍然使用原始的十字坐标系表示的)
2. 定义矩阵列的含义:基向量变换后的坐标
该 v v v的原始的坐标 相当于 告知了与原始基 i , j i,j i,j的线性关系
变换后的基向量 i i i 和基向量 j j j 的坐标与上图相同 — i : ( 1 , − 2 ) , j ( 3 , 0 ) i:(1,-2),j(3,0) i:(1,−2),j(3,0),向量 v v v变换后的坐标为:
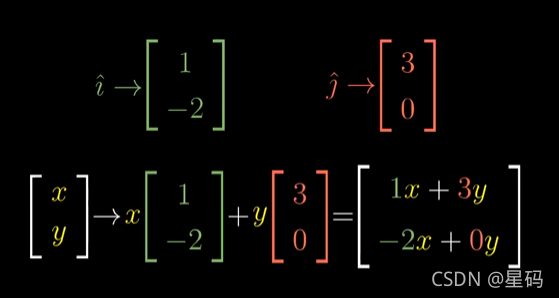
- 将变换后的i与j的坐标封装到一个矩阵中:
[ a b c d ] \begin{bmatrix} a & b\\ c & d\\ \end{bmatrix} [acbd]
由矩阵封装过程知:其中第一列为变换后的 i 的坐标(a,c),第二列为变换后的 j 的坐标(b,d) — 矩阵每一个列可以看成:基向量变换后的坐标
(由上述 向量 v 的一般形式 ( x , y ) (x,y) (x,y) 与 两个基向量变换后的坐标的关系)可以得到变换后的向量 v 的坐标:

3. 定义矩阵与向量的乘法:线性变换 作用于 给定的向量
计算 线性变换 作用于 给定的向量 的一种途径(即:求经过线性变换后的向量)
- 线性变换是操纵空间的一种手段,他保持网络线平行且等距分布,并且保持原点不动 — 这种变换可以用变换后的 基向量的坐标 表示
- 所以看到一个矩阵的时候,可以将其解读为对空间的一种特定的变换
矩阵每一个列可以看成:基向量变换后的坐标
而矩阵与向量乘可以看成:
- 对于 变换后的坐标 的 线性组合 来得到变换后的向量
- 也可理解为:线性变换 作用于 给定的向量 — 其实就是1换了一种说法
- 理由:因为v与i,j 与 变换后的v与变换后的i,j 有同样的线性组合
图中红色圈为变换后的基的坐标,蓝色线为对变换后的基进行线性组合要得到水绿色的那个向量(即变换后的向量)
二:矩阵与矩阵的乘法 - 线性变换复合
Shear:剪切矩阵;错切矩阵:
[ 1 1 0 1 ] \begin{bmatrix} 1 & 1\\ 0 & 1\\ \end{bmatrix} [1011]
1. 两个矩阵相乘:就是两个线性变换的相继作用
对向量:先进行旋转,再进行剪切这样的效果 与 这两个操作的复合变换结果应该相同

2. 对两个矩阵相乘的过程的两种理解
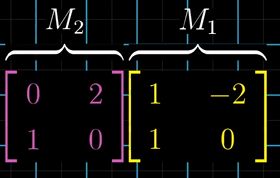
有 M 2 M 1 M_2 M_1 M2M1两个矩阵相乘
- 从图像角度: — 线性变换 先得到改变后的基向量,再由改变后的基向量得到改变后的向量
- 图中绿色的向量表示为原始基向量i变换后的位置
- 图中红色的向量表示为原始基向量j变换后的位置
角度1的解释:
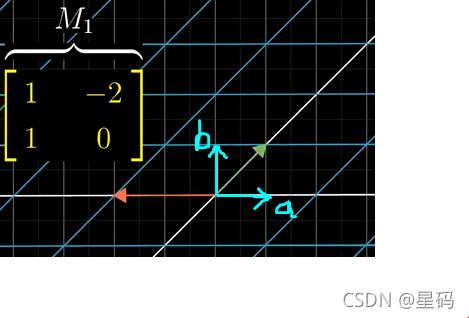
- 第一个与矩阵 M 1 M_1 M1作用,可以将基向量 i i i的坐标变换为 ( 1 , 1 ) (1,1) (1,1), j j j的坐标变换为 ( − 2 , 0 ) (-2,0) (−2,0)
注意,这个时候 i , j i,j i,j的坐标是相对于最原始的参考系而言的 - 也即我们熟悉的十字坐标系(图一中的水绿色画出的向量 a , b a,b a,b作为的参考系) - * 第二次与矩阵 M 2 M_2 M2作用,可以将 i , j i,j i,j看成一个普通向量
* 此时的变换是:将图一中水绿色的向量 a , b a,b a,b看成 — 图一的基向量, M 2 M_2 M2的每一列为图一基向量对应的坐标: a ( 0 , 1 ) , b ( 2 , 0 ) a(0,1),b(2,0) a(0,1),b(2,0),再由 M 2 M_2 M2改变后的基向量 a , b a,b a,b得到改变后的 i , j i,j i,j
* 这一过程就是:将 M 2 M_2 M2的线性变换 作用于 经过 M 1 M_1 M1改变后的普通向量 i , j i,j i,j上
- 从运算的角度 — 矩阵的线性变换直接对向量进行改变
- 对于原始基坐标 i , j i,j i,j经过 M 1 M_1 M1后得到变换后的 i ( 1 , 1 ) , j ( − 2 , 0 ) i(1,1),j(-2,0) i(1,1),j(−2,0)
- 下来直接让 M 2 M_2 M2的线性变换作用于 变换后的 i , j i,j i,j:
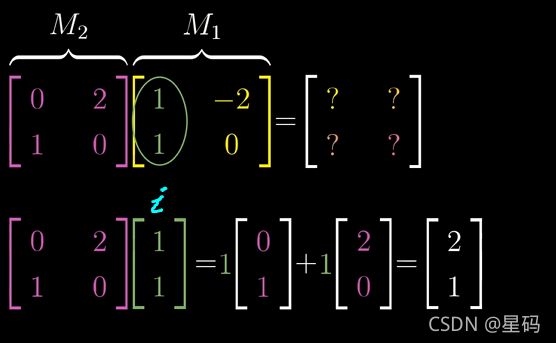
直接由一.3节定义的矩阵与向量的乘法得到经过 M 2 M_2 M2改变后的 i i i的坐标(同理可得改变后的 j j j的坐标)
3. 运算律
1. 矩阵相乘时,先后顺序会影响结果
绿色线为变换后的的基向量 i i i,红色线为变换后的基向量 j j j
先shear再rotation:

先rotation然后shear:

发现得到的结果不一样
2. 结合律(Associativity)
( A B ) C = A ( B C ) (AB)C=A(BC) (AB)C=A(BC)
- 等式左边: ( A B ) C (AB)C (AB)C作用于一个向量,相当于先让C作用,再让B作用,再让A作用
- 等式右边: A ( B C ) A(BC) A(BC)作用于一个向量,相当于先让C作用,再让B作用,再让A作用
4. 行列式 - 测量变换对空间有多少拉伸或挤压
1. 从二维与三维理解行列式
- 二维情况:
线性变换改变 面积 的比例 被称为 这个变换的行列式的绝对值
而行列式的正负表示变换后的空间是否被翻转 — 描述定向的改变
-
行列式为6,就是将一个区域的面积变为原来的6倍
-
当行列式为负值的时候, 直观感觉是将空间都翻转了
- 三维情况:
- 线性变换改变 体积 的比例 被称为 这个变换的行列式的绝对值
- 而行列式的正负表示变换后的空间是否被翻转 — 描述定向的改变(通过右手定理判断)
右手定理:右手食指指向i方向,中指指向j,大拇指指向k方向
* 如果变换后仍然可以用右手这么做,那么说明定向没有发生变换,行列式为正
* 如果变换后只能用左手这么做,说明定向发生变换,行列式为负
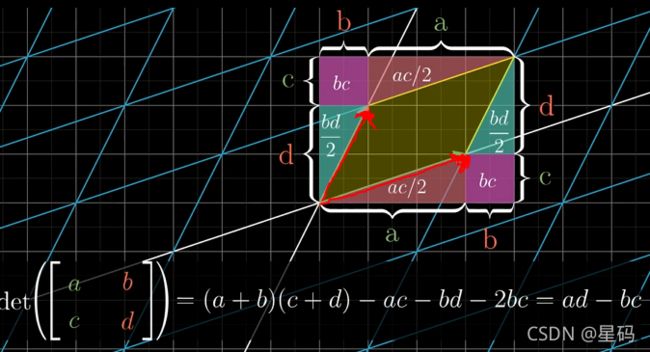
2. 如何计算行列式
二维:
三维:
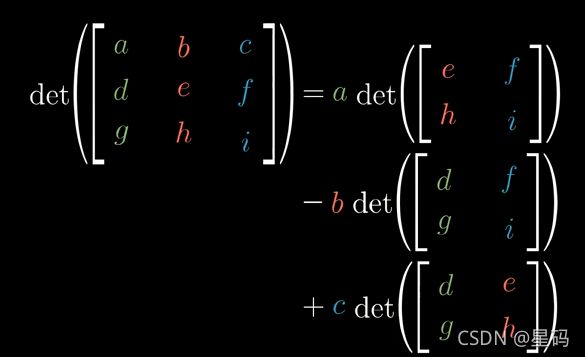
证明:

1.一个行列式相当于一次空间变换引起的面积变化
2.两个行列式相乘相当于进行了两次空间放缩,复合变换的缩放比例等于分别变换的缩放比例乘积
三:逆矩阵,列空间,零空间
线性代数在几乎所有领域中都有所体现并被广泛应用的主要原因是:可以帮助我们求解特定的方程组
矩阵 A A A代表一种线性变换
求解 A x = v Ax=v Ax=v相当于去寻找一个 x x x向量,在线性变换后与 v v v重合(即: x x x通过线性变换后到 v v v的位置)
1. A x = v Ax=v Ax=v 求解 x x x时 — 逆矩阵 与 行列式为0的理解
-
A x = v Ax=v Ax=v 当矩阵 A A A行列式不为0时
可以通过对 v v v做逆向变换就可以找到 x x x — 逆向变换对应另一个矩阵,被称为“逆”,记为 A − 1 A^{-1} A−1
A − 1 A A^{-1}A A−1A含义是:先线性变换,在做逆变换 — A − 1 A = A^{-1}A= A−1A=什么都不做的变换(恒等变换)
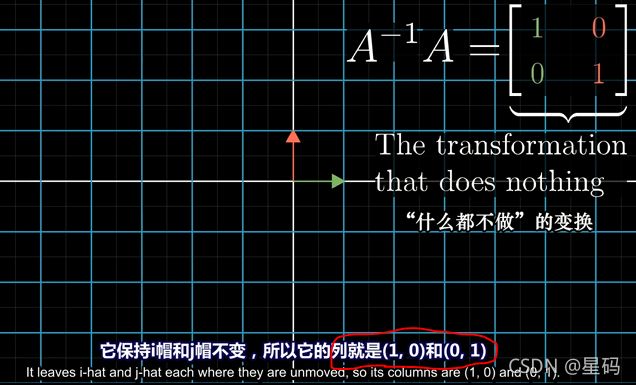
当找到 A − 1 A^{-1} A−1时:

将 v v v做逆变换(可以做逆变换,说明矩阵 A A A行列式不为0,有 A − 1 A^{-1} A−1),得到 x x x,此时 x x x是唯一解 -
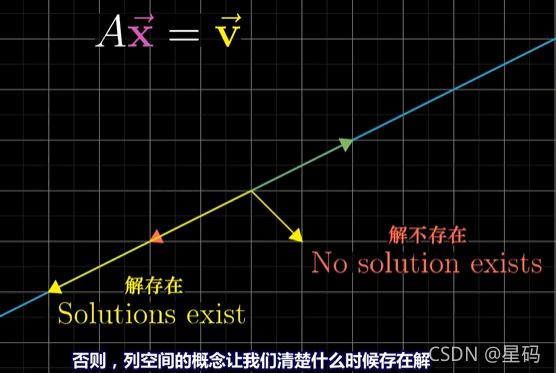
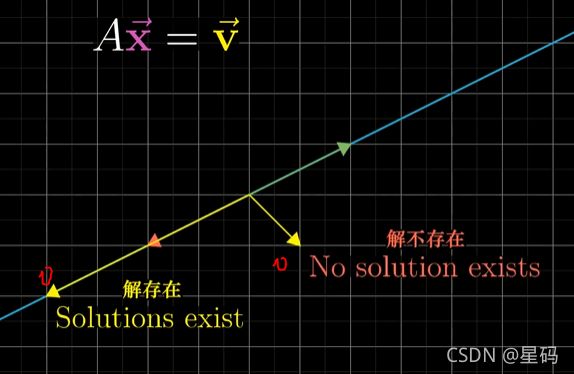
A x = v Ax=v Ax=v 当矩阵 A A A行列式为0时 — 变换将空间压缩到更低的维度上
此时不存在逆变换:不可以将低纬度空间拉伸到一个特定的高维空间 (类似不可以将一条线"解压缩"为一个平面)
但即便不存在逆变换,解仍然存在:(二维空间)一个变换将空间压缩到一条直线上
v v v如果恰好在这个直线上时,有解;如果 v v v不在这个直线上,则无解
2. Rank - 秩:变换后空间的维度/列空间的维数
- 当变换后向量在一条直线上时 — 结果为一维的:称这个变换的秩为1
- 当变换后向量在一个平面上时 — 结果为二维的:称这个变换的秩为2
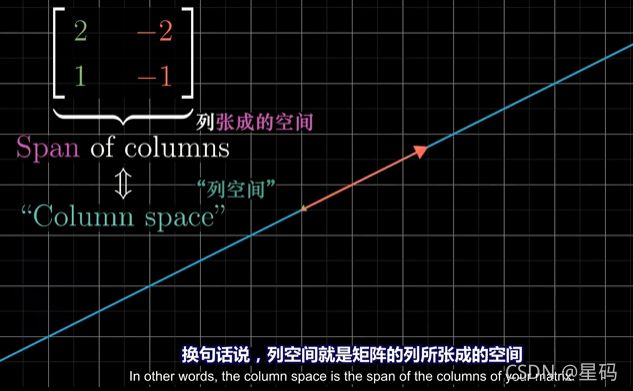
3. 列空间 — 矩阵的列所张成的空间

A A A列空间: A v ^ A\hat{v} Av^所有可能的输出向量的集合(即: A A A的列向量的线性组合)
矩阵的列可以得到基向量变换后的位置,这些变换后的基向量张成的空间(就是变换后的基向量 的线性组合得到的向量)就是所有可能的变换结果
图中的变换后的两个基向量共线,这两个基向量 所张成的空间(向量的线性组合) 在一条直线上
换句话说:列空间就是矩阵的列所张成的空间
∴ \therefore ∴更精确的秩的定义是:列空间的维数:因为列空间的维数 — 变换后基向量所张成的空间(向量的线性组合后)的维数,也即:变换后空间的维度
- 对方阵(方阵的理由在文章开头)来说,满秩意味着:秩与列数相等
矩阵有几列说明有几个基向量(即原始空间是几维)
秩与列数同时,意味着:变换后基向量所张成的空间与原始空间相同,所以为满秩
4. 零空间 — 变换后的向量 落在零向量上的 向量的集合
零向量一定在列空间中(因为线性变换必须保持原点位置不变)
- 对于满秩(Full rank)变换来说,唯一能在变换后落在原点的就是零向量本身
- 对于非满秩的变换,空间被压缩到一个更低的维度上,也就是说:会有一系列向量在变换后成为零向量:(演示变换的参考视频)
- 如果一个二维线性变换将空间压缩到一条线,那么沿着某个不同方向直线上的所有向量被压缩到原点
(there is a separate line in a different direction full of vectors that get squished onto the origin) - 如果一个三维线性变换将空间压缩到一个平面,会有一整条线上的向量在变换后落在原点
如果一个三位线性变换将空间压缩到一条直线,有一整个平面上的向量在变换后落在原点
- 如果一个二维线性变换将空间压缩到一条线,那么沿着某个不同方向直线上的所有向量被压缩到原点
变换后落在原点的向量集合被称为矩阵的"零空间"(Null space)或"核"(Kernel):变换后一些向量落在了零向量上,而零空间就是这些向量所构成的空间
- 对其次方程组来说 A x = 0 Ax=0 Ax=0(即:向量 v v v为零向量):
零空间给出的向量集合就是这个向量方程的所有可能的解 — 因为经过变换后这些向量落在了零向量上
这个现象可以用来解释为什么系数矩阵满秩的齐次方程只有0解,而不满秩的其次方程有一个基础解系
- 满秩时:变换后的空间维数不变,则唯一能在变换后落在原点的就是零向量本身,即只有0解
- 不满秩时:变换后的空间维度减小,会有一系列向量在变换后成为零向量,即有一个基础解析
5. 综合 — 从几何角度求解线性方程组:从逆矩阵,列空间,零空间
线性方程组: A x = v Ax=v Ax=v对应一个线性变换
-
如果该变换有逆变换时,就可以使用这个逆变换进行求解方程组
-
如果逆变换不存在
-
零空间概念有助于我们理解所有可能的解的集合是什么样的(对于齐次方程组而言 A x = 0 Ax=0 Ax=0求解)
四:非方阵几何含义 — 不同维度的映射
讨论不同维度直接的变换是合理的:

将矩阵的列视为:变换后的基向量坐标
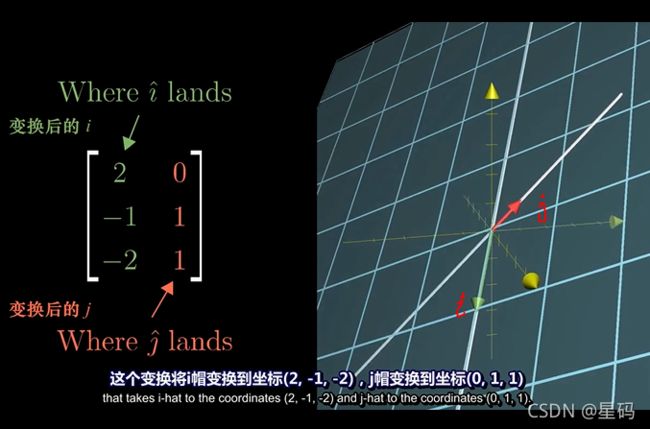
这个矩阵是 3 × 2 3\times2 3×2:
列数为2:说明原始空间中有两个基向量
矩阵的列为对应变换后基向量的坐标
行数为3:说明变换后基向量的坐标到了3维(每个变换后的向量用三个独立的坐标来描述)
也即:两个原本在二维空间的基向量被映射到了3维空间
这个矩阵的列空间是三维空间中过原点的二维平面:映射到三维空间后,图中两个向量方向不同,两个不同方向向量的线性组合为平面
∴ \therefore ∴ 这个矩阵是满秩的:因为列空间的维数与输入空间的维数相等:列空间维数是2,输入空间维数也是2
这个矩阵是 2 × 3 2\times3 2×3:
列数为3:说明原始空间中有三个基向量
矩阵的列为对应变换后基向量的坐标
行数为2:说明变换后基向量的坐标到了2维(每个变换后的向量用两个独立的坐标来描述)
也即:两个原本在三维空间的基向量被映射到了二维空间
五:点积与其对偶性
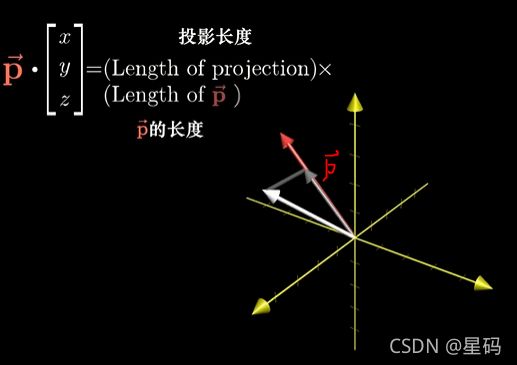
1. 点积与其几何解释 — 正交投影后长度相乘,正负与两个向量朝向有关
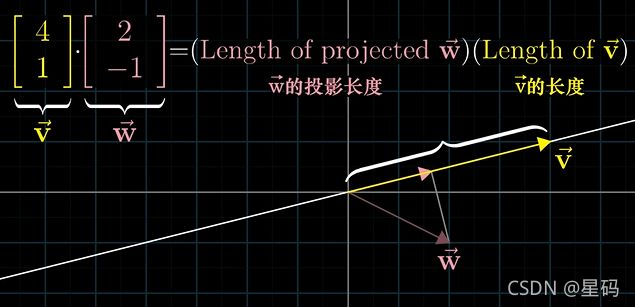
[ 4 1 ] ⋅ [ 2 − 1 ] = 4 ∗ 2 + 1 ∗ ( − 1 ) = 7 \begin{bmatrix} 4 \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 2 \\ -1 \\ \end{bmatrix} = 4*2+1*(-1) = 7 [41]⋅[2−1]=4∗2+1∗(−1)=7
点积的含义 — 向量 w w w朝着 向量 v v v 正交投影,投影的长度与向量 v v v的长度相乘,而正负与 w w w的投影和 v v v方向有关
点积的含义:向量 w w w朝着 过原点和向量 v v v终点的直线上 正交投影,将投影的长度与向量 v v v的长度相乘,而正负与 w w w的投影和 v v v方向有关( w w w投影到 v v v与 v v v投影到 w w w效果一样)
- 当两个向量的指向基本相同时:点积为正
- 当两个向量的指向垂直时:点积为0
- 当两个向量的指向基本相反时:点积为负
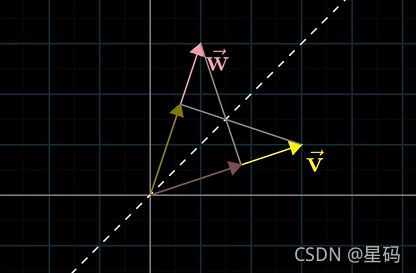
点积与投影顺序无关,即: w w w投影到 v v v与 v v v投影到 w w w效果一样 — 演示视频
一个向量为 v v v,一个向量为 w w w,两个向量的长度相同
此时 w w w向 v v v的投影与 v v v向 w w w的投影相同,即这个情况说明了点积与投影顺序无关
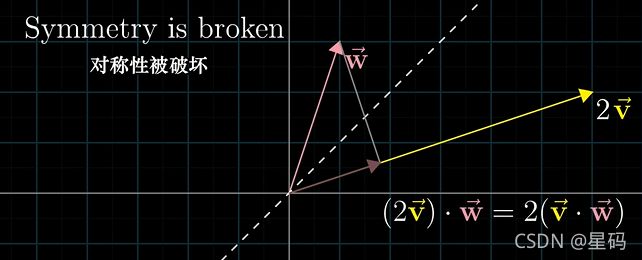
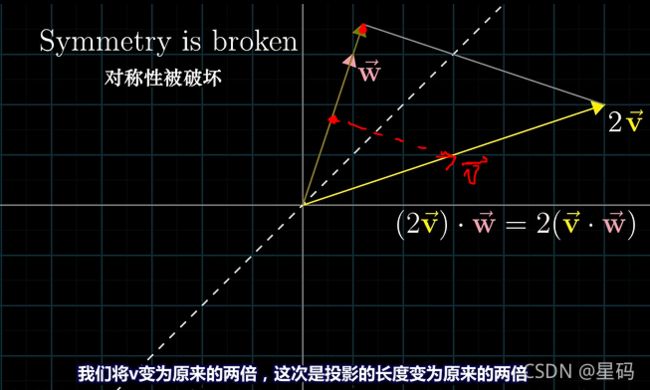
当 v v v —> 2 v 2v 2v时,以下证明点积与顺序无关
w w w投影到 2 v 2v 2v向量上,投影长度固定与 w w w投影到 v v v向量上相同,而 v v v长度变成了 2 v 2v 2v的长度,所以最后的结果为2倍的 v ⋅ w v \cdot w v⋅w
将 2 v 2v 2v投影到 w w w上,投影长度是 v v v向量投影到 w w w向量的两倍,向量 w w w长度不变,所以最后的结果为2倍的 v ⋅ w v \cdot w v⋅w
2. 对偶性(duality):点积 与 对应坐标相乘并相加 之间的联系
1. 线性变换简化成一个等价的直观特性
高维空间中的变换需要满足一些严格的特性才会具有线性 — 保持网络线平行且等距分布,并且保持原点不动
这个条件可以简化成一个等价的直观特性:
2. 向量 线性变换为数 与 映射矩阵对应向量 存在的关系:应用映射矩阵线性变换 和 与映射矩阵对应的向量(对偶向量)做点积 是一样的结果
将向量线性转化为数的线性变换与这个向量本身有着某种关系 — 演示视频

-
[ u x u y ] \begin{bmatrix} u_x \\ u_y \\ \end{bmatrix} [uxuy]为对应的单位向量 u u u的坐标,其是一个二维向量,但其正好落在了我们定义的要变换到的一维数轴上,所以变换后还是一维数组的单位向量
-
[ u x , u y ] [u_x,u_y] [ux,uy]称为映射矩阵(变换矩阵),这是与 u u u相关的,后续会有求出该映射矩阵过程
-
由上图计算可以看到图中 1 × 2 1 \times 2 1×2矩阵与二维向量相乘的计算过程 和 矩阵对应的向量(对偶向量)与二维向量求点积的过程相同,所以这个投影变换必然和某个二维向量相关
以下来寻找图中投影矩阵与向量相乘的含义
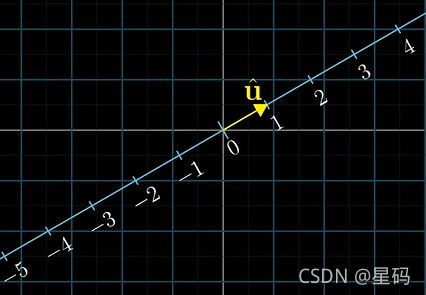
将二维平面线性转化到图中的直线上,假设该 一个单位长度的向量称为 u u u 是一个二维向量,但其正好落在了我们定义的要变换到的一维数轴上
当然这个变换是线性的,因为可以由上面的等价的直观特性得到
单位向量 u u u的坐标为 [ u x u y ] \begin{bmatrix} u_x \\ u_y \\ \end{bmatrix} [uxuy],此时投影矩阵为 [ u x , u y ] \begin{bmatrix} u_x, u_y \end{bmatrix} [ux,uy] 的证明:此时的投影矩阵是 1 × 2 1 \times 2 1×2(每列对应变换后的基坐标,1行说明变换后坐标用一个数表示),下来求这个投影矩阵(即:找到基坐标变换后的坐标):
如图对称轴可以得到: i i i映射到 u u u上与 u u u映射到 x x x上的长度是一样的,所以 i i i变换后为 u x u_x ux
同理可得 u u u映射到 j j j的长度,所以得到变换后的 j j j
- 投影矩阵与向量相乘的意义是:将变换运用到向量上 — 由上述演示即:将向量投影到对应的直线上
空间中任意一个向量经过变换后的结果就是:投影矩阵与这个向量相乘,由本节开始计算过程发现 映射矩阵与向量相乘 和 向量和向量 u u u的点积 的结果相同(此时假设的 u u u为单位向量)
- ∴ \therefore ∴ 与单位向量的点积可以解读为 — 将向量投影到单位向量所在的直线上的所得到的投影的长度
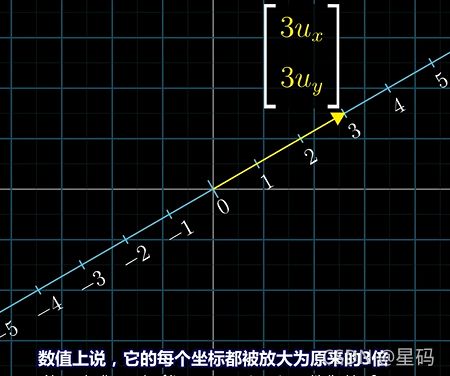
将二维平面线性转化到图中的直线上,假设 一个3倍单位长度的向量称为 3 u 3u 3u 是一个二维向量,但其正好落在了我们定义的要变换到的一维数轴上
当然这个变换是线性的,因为可以由上面的等价的直观特性得到
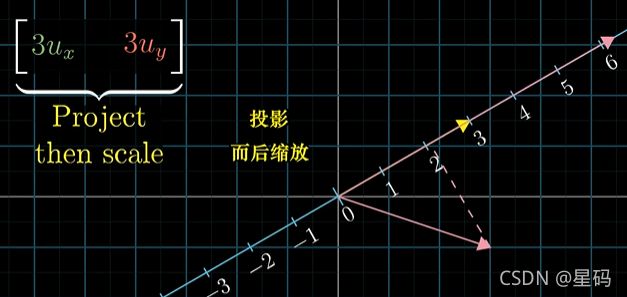
向量 3 u 3u 3u的坐标为 [ 3 u x 3 u y ] \begin{bmatrix} 3u_x \\ 3u_y \\ \end{bmatrix} [3ux3uy],投影矩阵为 [ 3 u x , 3 u y ] \begin{bmatrix} 3u_x, 3u_y \end{bmatrix} [3ux,3uy]:数值上说,这个 3 u 3u 3u向量 相对于 u u u向量 而言,它的每个坐标都被放大了原来的3倍,所以要寻找这个向量相关的投影矩阵 — 实际上就是 i , j i,j i,j投影得到的值的3倍
3 u 3u 3u向量对应的投影矩阵 的线性变换 是线性的,所以投影矩阵可以看作:将任何向量朝斜着的一维轴投影,再将结果乘以3空间中任意一个向量经过变换后的结果就是:投影矩阵与这个向量相乘,由本节开始计算过程发现 3 u 3u 3u对应映射矩阵与向量相乘 和 向量和向量 3 u 3u 3u的点积 的结果相同(此时假设的 3 u 3u 3u为3倍的单位向量 u u u)
- ∴ \therefore ∴ 与3倍的单位向量的点积可以解读为 — 将向量投影到3倍的单位向量所在的直线上的所得到的投影的长度,再乘以3
∴ \therefore ∴ 任意向量与非单位向量的点积 可以理解为:首先朝 给定向量投影,再将投影的值与给定向量长度相乘
3. 过程总结,对偶性,与点积含义
过程总结:
有一个从二维空间到数轴的线性变换,其不是由向量数值或点积运算定义的,是通过将空间投影到给数轴定义
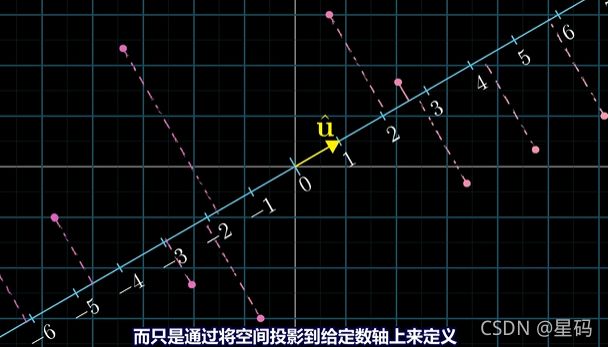
因为这个变换是线性的,所以可以使用 1 × 2 1 \times 2 1×2矩阵描述,又因为 1 × 2 1 \times 2 1×2矩阵与二维向量相乘的计算过程 和 转置矩阵与向量求点积的过程相同,所以这个投影变换必然和某个二维向量相关

所给的启示:在看到任何一个线性变换,他是输出是一个一维数轴,无论其如何定义,空间中一定存在唯一一个向量 v v v与之相关 — 即:应用线性变换 和 与向量 v v v做点积 是一样的结果
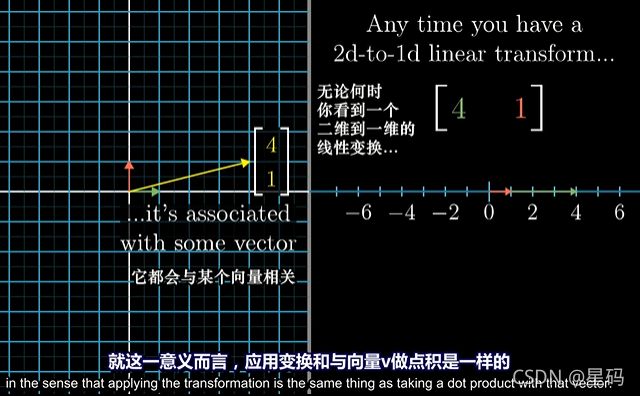
对偶性(duality):
点积:
- 两个向量的点积 与 对应矩阵和向量相乘 结果一样

- 点积是理解投影的有效工具,并且方便检验两个向量的指向是否相同
- 两个向量点乘 就是 将其中一个向量转化为线性变换(此时这个向量不仅仅是空间中的箭头,而是线性变换的载体)
六:叉积
先介绍叉积的标准介绍,再通过线性变换深入理解 — 叉积参考视频
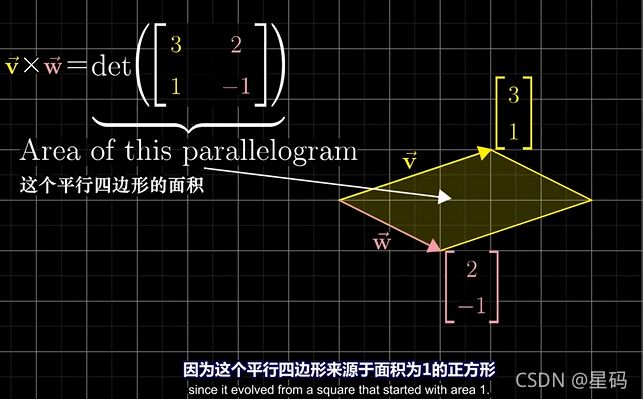
1. 叉积的介绍与计算 — 两个向量围成平行四边形面积与长度同,方向遵循右手定则的一个向量
二维空间时:(这里的描述不是严格定义的叉积)
v , w v,w v,w两个二维向量
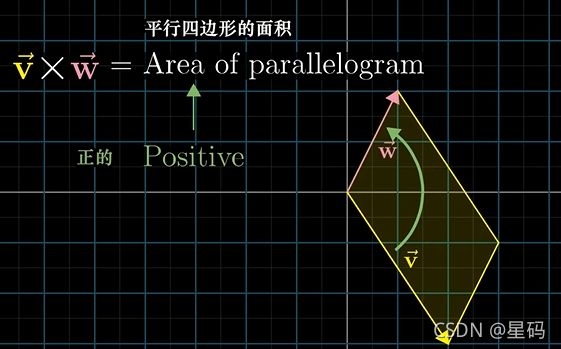
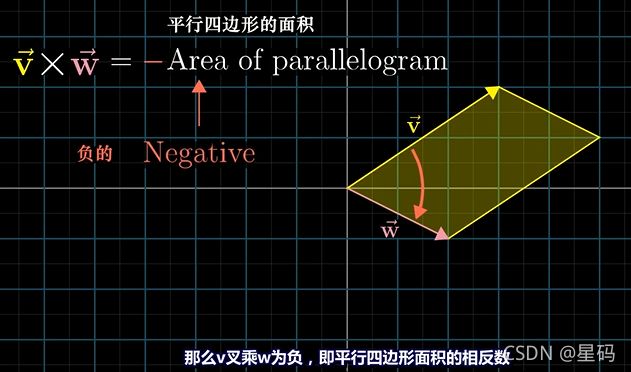
- 他们的叉积 v × w v \times w v×w的绝对值: 就是这两个向量组成的平行四边形
- 而方向: 如果 v v v在 w w w的右侧,则其叉积为正;如果在左侧,则值为负
如何求正负:
这个顺序记忆的方法:
当按序求两个基向量的叉积:即 i i i叉乘 j j j( i × j i \times j i×j) 结果应该是 — 正1.
- 实际上,基向量的顺序就是定向的基础:因为 i i i在 j j j的右侧,所以答案为正
如何求平行四边形面积: — 行列式[也同时求得了叉积的正负](在第二章第4节)
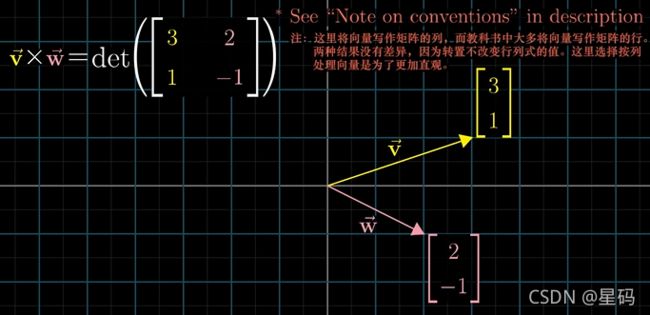
叉积 v × w = v \times w= v×w=:将 v , w v,w v,w的坐标组成行列式各列,直接计算行列式,这样可以得到对应 面积值 还有 正负号
- 如此计算是因为:
- 由 v , w v,w v,w的坐标为列构成的矩阵,与一个将 i , j i,j i,j分别变换到 v , w v,w v,w的线性变换对应 — 之前内容:矩阵的列为 i , j i,j i,j变换后的矩阵
- 而行列式就是变换前后面积变换的度量, 而行列式的正负表示变换后的空间是否被翻转 — 描述定向的改变
这个过程就变成了:开始是变换前的 i . j i.j i.j,他们所构成的为单位为1 的正方形,而经过线性变换后, i , j i,j i,j的位置变成了我们需要的 v , w v,w v,w,而其原来的单位为1的正方形变成了我们现在所关系的平行四边形,而行列式:可以描述面积的变化 以及 定向的变化
以上虽然描述了叉积,但不是真正意义上的叉积,只是为了引入,所以之后不再使用以上进行计算叉积
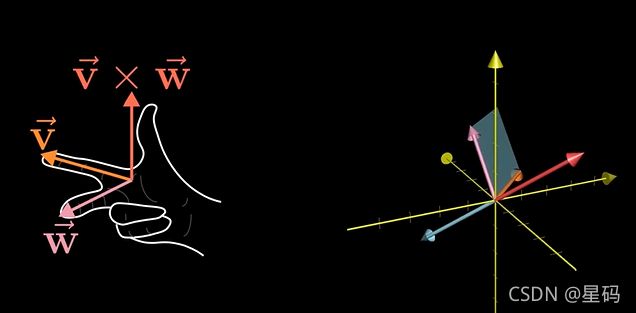
真正的叉积是通过两个三维向量生成一个新的三维向量
叉积首先是一个向量 v ⃗ × w ⃗ = p ⃗ \vec{v} \times \vec{w} = \vec{p} v×w=p
计算叉积:
- 此时求出的向量(叉积) 是为一个 值与 v , w v,w v,w围成平行四边形面积相同,方向与 v , w v,w v,w垂直且遵循右手定则 的向量
2. 叉积对偶性 — 叉积所得向量几何意义是对偶向量
上一节讲了如何计算,但为什么需要这样计算?如果要理解这些,需要用到第五章第2节的对偶性 — 参考视频
-
对偶性的回顾:
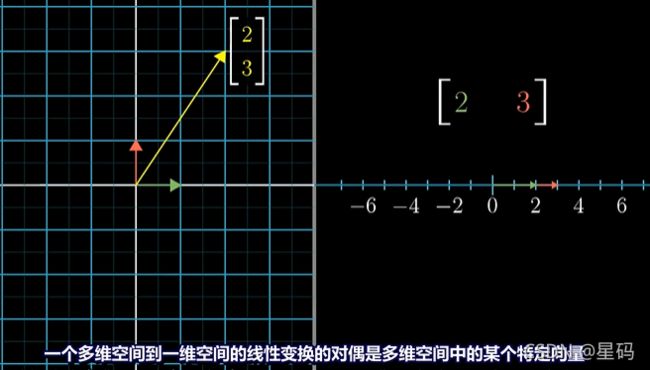
对偶性的含义:每当看到一个多维空间到数轴的线性变换时,它都与那个空间中的唯一一个向量对应(这个向量称为这个变换的对偶向量),即:应用线性变换 和 与这个向量点乘等价
-
定义一个函数来理解:
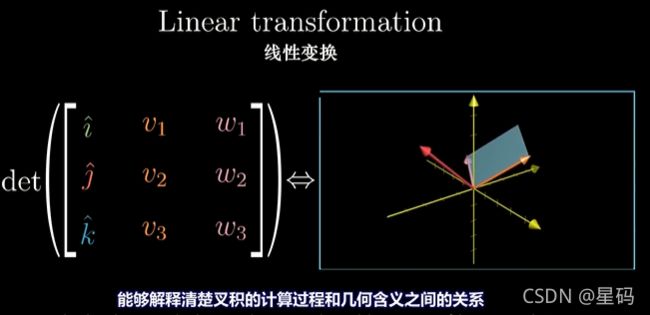
定义一个函数:输入是三维空间一个向量,然后通过矩阵的行列式得到一个数。(这个矩阵第一列为输入的向量,第二列,第三列为向量 v , w v,w v,w)
这个函数的几何意义为:对应任何输入的向量 ( x , y , z ) (x,y,z) (x,y,z)都考虑由它和 v , w v,w v,w确定的平行六面体,得到他的体积(由行列式的意义得),然后根据定向确定符号
这个函数是线性的(来个笨方法:把函数当成变换看,行列式展开后能明显看出来线性变换的可加性和成比例的性质),所以才可以引进对偶性的思想
上面定义的函数是线性的,所以可以使用矩阵乘法来描述这个函数,并且找到对应的对偶向量
而我们要找的叉积就是:这个特殊的三维向量,我们称为 p p p
要使得 p p p与其他任意向量 ( x , y , z ) (x,y,z) (x,y,z)的点积等于一个 3 × 3 3 \times 3 3×3的矩阵的行列式 — 这个矩阵第一列为 ( x , y , z ) (x,y,z) (x,y,z)其他两列为 v , w v,w v,w的坐标
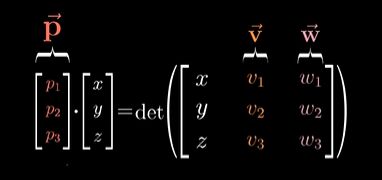
下来讨论定义函数变化的计算意义和几何意义
(1) 叉积的计算意义:
展开点积和行列式,可以得到 p p p各个坐标
总结来说:
求一个向量 p p p,这个向量 p p p和某个向量 ( x , y , z ) (x,y,z) (x,y,z)点乘时,所得的结果等于一个 3 × 3 3 \times 3 3×3的矩阵的行列式 — 这个矩阵第一列为 ( x , y , z ) (x,y,z) (x,y,z)其他两列为 v , w v,w v,w的坐标
(2) 叉积的几何意义:
由计算意义和行列式的意义(三维时,行列式表示体积的变化,而变化前体积为1[基向量 i , j , z i,j,z i,j,z围成体积为1])得:
将 p p p和某个向量 ( x , y , z ) (x,y,z) (x,y,z)点乘时,所得的结果等于一个由 ( x , y , z ) (x,y,z) (x,y,z)和 v , w v,w v,w确定的平行六面体的体积
点积回顾:
回顾点积那章,向量 p p p和其他向量的点积的解释:是将其他向量投影到 p p p上,然后将投影长度和 p p p的长度相乘
对于我们关系的平行六面体的体积
还记得在最开始我们定义的 线性函数吗,按照上面我们对平行六面体的体积描述,我们对于那个线性函数换一个说法:
- 找到的线性函数 对于 给定向量的作用,是将这个向量 投影到 垂直于 v , w v,w v,w的直线上,然后将投影长度于 v , w v,w v,w组成平行四边形面积相乘
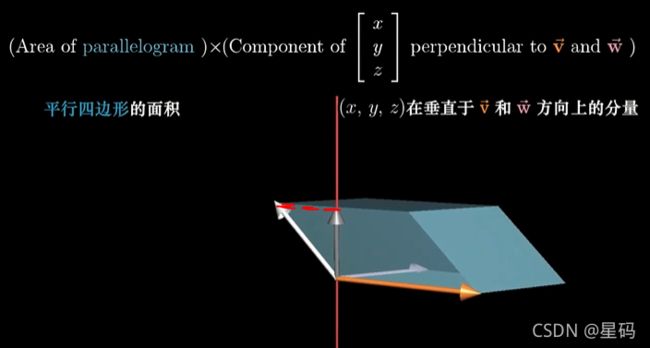
- 但这和垂直于 v , w v,w v,w且长度为平行四边形面积的向量 与 ( x , y , z ) (x,y,z) (x,y,z)点乘是一回事(具体看点积回顾)
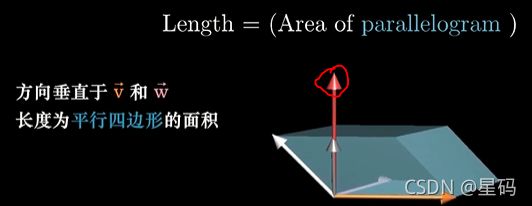
而垂直于 v , w v,w v,w且长度为平行四边形面积的向量就是我们所找的向量 p p p
这意味着我们找到了向量 p p p和某个向量 ( x , y , z ) (x,y,z) (x,y,z)点乘时,所得的结果等于一个 3 × 3 3 \times 3 3×3的矩阵的行列式 — 这个矩阵第一列为 ( x , y , z ) (x,y,z) (x,y,z)其他两列为 v , w v,w v,w的坐标
(3) 总结:
之前通过计算得到的 p p p的坐标
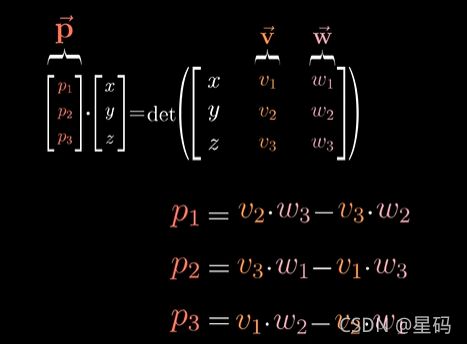
必然在几何上与这个向量对应

这就是叉积的计算过程和几何解释有关联的根本原因
这两种方法分别是:
方法1.用几何方法推出p的大小为vw张成面积,方向为垂直vw面。
方法2:整理行列式的计算式子使得表达式等于p与xyz的点积,那么p就求出了,因为是同一回事,所以两种方法是在求同一向量
参考视频
【官方双语/合集】线性代数的本质 - 系列合集:https://www.bilibili.com/video/BV1ys411472E?p=1