线性代数的本质(3Blue1Brown视频整理)
向量:看做一种特定的运功
基本操作:
- 向量加法:两种运动的组合 对应项相加
- 向量数乘:缩放向量
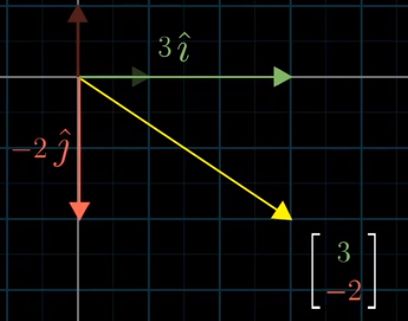
每个向量可看做对 i, j 向量缩放并相加。 i, j 向量 合称为二维坐标系的基向量
线性组合:两个数乘向量的和
张成空间:所有线性组合构成的向量集合
在二维空间中:
- 当向量不共线时,张成空间为平面所有二维向量的集合。
- 向量共线时,张成空间就是一条直线上的向量集合 (同为0向量除外)。
线性相关: 在一组向量中,若有一个向量
- 对张成空间没有贡献,即不增加该组向量的张成空间
- 可表示为其它向量的线性组合
则该组向量线性相关。反之,每个向量都为张成空间增加了新的维度,则它们线性无关。
基:张成该向量空间的一个线性无关向量集。
.
线性变换:严格上讲,是以向量为输入和输出的一类函数。可看作操纵空间的一种手段:
- 保持原点不动
- 网格线保持平行且等距分布(任意一条直线在变换后仍是一条直线)

一个二维线性变换仅由四个数字完全确定:i, j 变换后的坐标 [a, c], [b, d], 可看作新的基向量

如果变换后的基向量是线性相关的,那么这个线性变换将整个二维空间挤压到一条直线上。
将看到的每个矩阵都理解为空间的一种特定变换,矩阵向量乘法就是计算线性变换作用于定向量的一种途径。
对给定向量先旋转后剪切,相当复合变换。因此将该复合矩阵看作剪切矩阵和旋转矩阵的乘积是合理的。
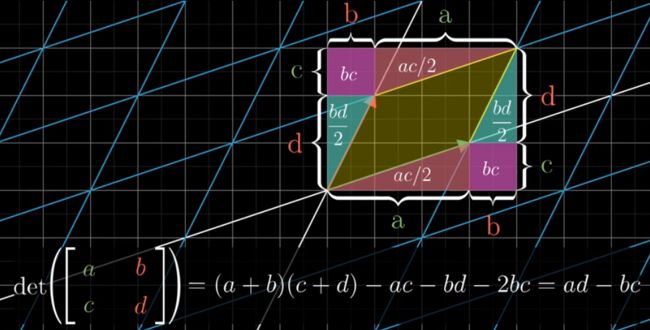
行列式:线性变换面积改变的比例
由于网格线保持平行且等距分布,只需观察单位正方形面积改变比例即可。
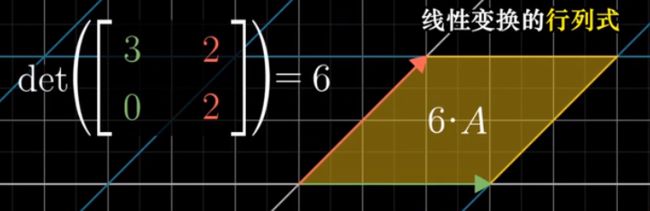
行列式为0,意味着将空间压缩到更小的维度上。
行列式为负,意味着空间定向发生了改变(变换中 i, j 交错),绝对值仍为面积改变比例。
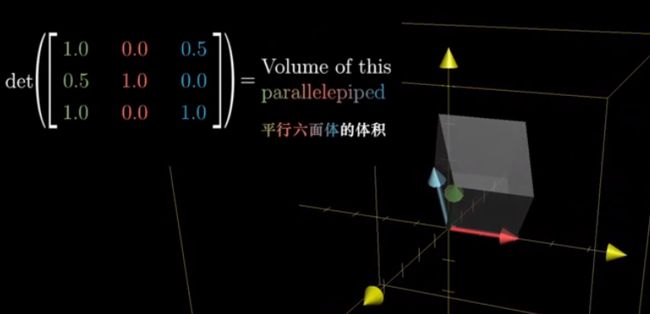
三维空间中,行列式代表平行六面体的体积。
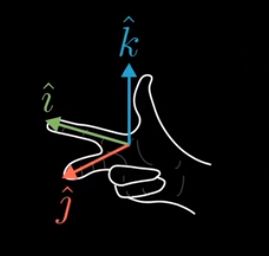
三维空间的空间定向:右手定则。
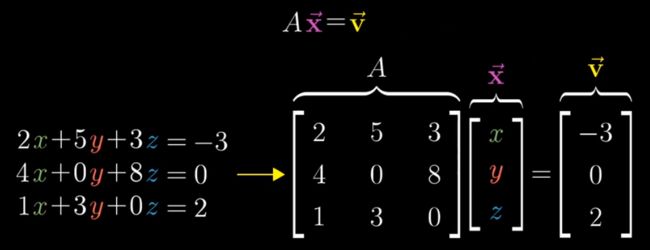
求解方程组,相当于寻找一个向量x,使得它在线性变换后与v重合。
当A行列式不为0时,追踪A的逆变换,可得唯一解x,通过左乘A逆求解。
逆矩阵:原矩阵的逆变换,同时作用相当于恒等变换(什么都不做)。
当 A 行列式为0时,空间被压缩到更低的维度上,此时没有逆变换(线性变换不可能将一个点解压为一条线)。
但仍可能有解,当 v 恰好落在压缩后的空间时。
列空间:矩阵的列所张成的空间
秩:代表变换后空间的维数,即列空间的维数。
满秩:秩 = 列数
零空间、核:变换后落在原点的向量集合
基变换
Jennifer坐标系的值 --> 我们坐标系的值
我们对Jennifer坐标系向量的误解 --> 她真正想表示的向量: 左乘基变换矩阵
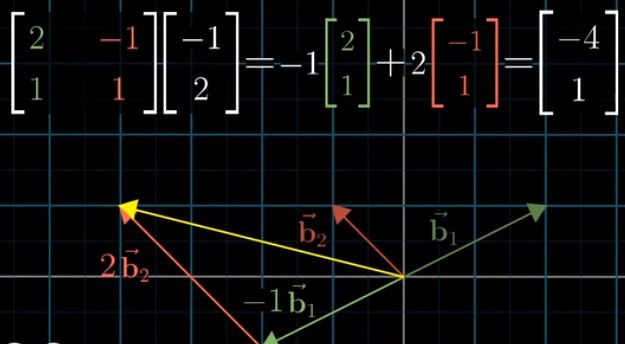
我们坐标系的值 --> Jennifer坐标系的值:左乘基变换矩阵的逆

如何用Jennifer语言描述变换矩阵:
左乘基变换矩阵(转化为我们语言) --> 在我们坐标系下左乘变换矩阵 --> 左乘基变换矩阵的逆(转化为Jennifer语言)


特征向量:在线性变换中,停留在自己所张成的直线空间,只发生拉伸或压缩,并未发生旋转的向量。
特征值:特征向量拉伸或压缩的比例因子。
作用:理解线性变换应当较少依赖于特定坐标系,观察特征向量和特征值是更好的方法。

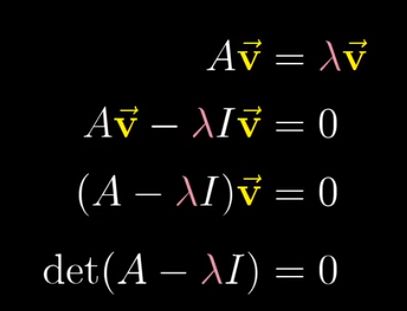
当 λ 取到特征值时,(A-λI) 的行列式为0,即对应的变换将空间压缩到更低的维度上。
此时存在非0特征向量 v ,在变换后被压缩成0向量。
特征基:一组基向量(同时恰好是特征向量)构成的集合。为对角矩阵,对角元为对应特征值。
当特征向量足够多,能张成全空间时,就可以用基变换转化为特征基,对角矩阵能大大简化矩阵运算。