Gradient Descen-univariate(吴恩达机器学习:梯度下降在线性模型的应用)
梯度下降算法在Linear Regression中的应用
文章目录
- 梯度下降算法在Linear Regression中的应用
-
- 单变量(univariate)
-
- 题目:预测利润
- 处理Training set
- 输入输出的数据提取并转换成矩阵形式
- 损失函数求解
- 梯度下降算法
- 可视化
- 预测
单变量(univariate)
题目:预测利润
(吴恩达机器学习课后题链接放在最后)

输入:城市人口数
输出:利润
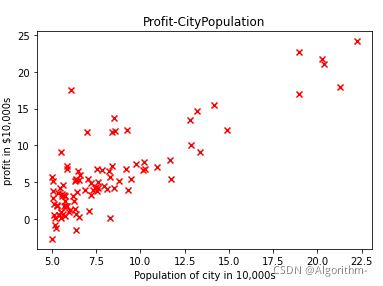
Training set

第一列为城市人口数,即输入
第二列为利润,即理想输出
处理Training set
file = pd.read_csv('E:/吴恩达机器学习/machine-learning-ex1/ex1/ex1data1.txt', header=None, names=['population', 'profit'])
# scatter绘制散点图
plt.scatter(file['population'], file['profit'], color='red', marker='x')
plt.title('Profit-CityPopulation')
plt.xlabel('Population of city in 10,000s')
plt.ylabel('profit in $10,000s')
运行结果如下
在梯度下降中,为了把theta_0加入到权重中进行矩阵运算,我们通常会在输入X的第一列插入全1列,可用以下代码实现:
file.insert(0, 'ones', 1)
loc为位置索引,这里是第0列;
column为列名,这里是’ones‘;
value是插入值,这里是1。
输入输出的数据提取并转换成矩阵形式
cols = file.shape[1] # 提取file的列数
X = file.iloc[:, 0:cols-1]
y = file.iloc[:, cols-1:cols] # 注意一定要切片,否则y变matrix后维数是(1,97)
m = len(y) # m= 97
# 转成矩阵形式
X = np.matrix(X.values)
y = np.matrix(y.values)
把切片得到的Dataframe或Series转换成矩阵,方便以后进行矩阵相乘和切片等操作。
注意此时的X和y为二维矩阵。
X的维数为(97, 2),y的维数为(97, 1),X中有插入的一列全1列,模型仍为单数入单输出。部分X数据和y数据如下:
输入X(含一列全1列)

输出y

损失函数求解
首先定义权重theta、学习率alpha、迭代次数iterations
theta = np.matrix(np.array([[0], [0.5]]))
iterations = 1500
alpha = 0.005
theta定义为 (2, 1)的数组,这里把theta_0和theta_1设置成不同的值,防止在梯度下降中两个权重值始终相同。
根据NG老师所讲,alpha最好要以3倍数来调整(增大或减小3倍)。
以下是损失函数CostFunction求解代码:
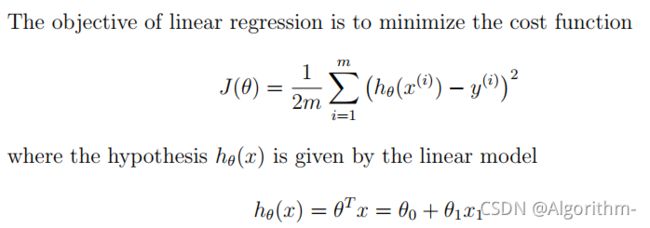
def computeCost(X, y, theta):
J_theta = 0
for i in range(m):
J_theta += (X[i, :] * theta - y[i]) ** 2
J_theta = J_theta / (2 * m)
return J_theta
对X的每一行与theta矩阵相乘(此前定义np.matrix(),矩阵相乘可以直接用*),之后与相应的训练集的理想输出进行做差,然后平方,最后把平方项相加,除以2m即可得到损失函数。
计算损失函数的一种更好的方式为向量方式,将会在多变量的线性回归中说明。
在初始权重theta的时候,我们调用损失函数查看运行结果:
J_theta = computeCost(X, y, theta) # 计算代价函数
运行结果:
梯度下降算法

注意,梯度下降是不断更新权重theta,并不是更新X或y,之后权重会影响模型的预测效果,而与输入输出无关。
对每一个权重theta,更新时刻为累加完所有的m个代数值后,所得累加值在与学习率alpha和样本数据m进行运算后才进行theta更新。
def gradientDescent(X, y, theta, alpha, num_iters):
J_history = np.zeros((num_iters, 1))
for iter in range(num_iters):
diff = X*theta - y
gradient_cost = (1/m) * (X.transpose()*diff)
theta = theta - alpha*gradient_cost
J_history[iter] = computeCost(X, y, theta)
return theta, J_history
定义了一个记录每次更新权重完成后损失函数值的变量J_history,可以在迭代完成后可视化梯度下降的效果,在每一次更新theta值之后,用新的theta值计算代价函数并存放在J_history中。

diff为 ( h_theta(x) - y ),为(m, 1)维。其中的每一行都是某一训练集样本中预测输出与实际输出的差值。
在算法公式中,每一个权重theta_j最后对应需要乘一个X_j,而X是(m,2)维,每一列是一个X_j在不同训练集样本输入下的列向量;每一行为一个训练集样本。所以可以考虑把X转置,之后再与diff进行矩阵相乘,所得结果为(2, 1)矩阵,其中的值等于对应的theta的算法中的求和部分。求出的结果再与alpha和m进行运算,得到theta的更新部分。
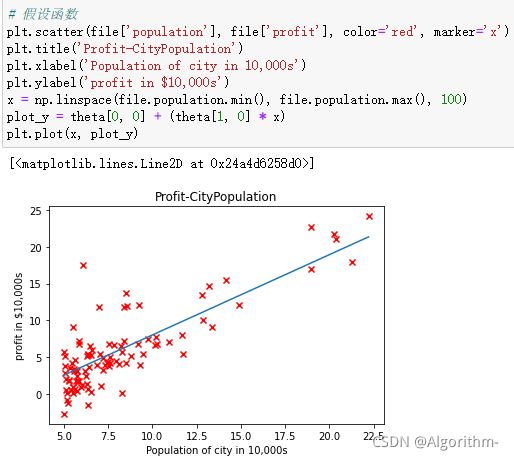
可视化
该部分要绘制代价函数随迭代次数而变化的曲线和模型训练完后的假设函数h_thtea。代码如下:
# 代价函数
plt.figure()
plt.plot(np.arange(iterations), J_history)
# 假设函数
x = np.linspace(file.population.min(), file.population.max(), 100)
plot_y = theta[0, 0] + (theta[1, 0] * x)
plt.plot(x, plot_y)
结果如下:
横坐标为迭代次数,纵坐标为代价函数。
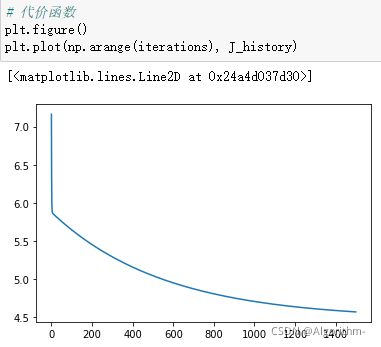
横坐标为城市人口数,纵坐标为利润
预测
def pridicit(population,theta):
X = np.matrix([1, population])
return (X * theta)
传入参数:城市人口数和权重theta。
输出:利润。
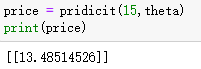
price = pridicit(15,theta)
print(price)
篇幅限制,多变量部分放在另一个文章里,点击这里跳转。
欢迎评论区留言讨论。
NG Machine Learning Courses
链接:https://pan.baidu.com/s/1FoAQNRdevsqYzW4a5QDsBw
提取码:0wdr