算法设计与分析 实验二 分治法求解最近点对问题

一、实验目的与要求

1、实验基本要求

（1） 掌握分治法思想。
（2） 学会最近点对问题求解方法。

2、实验亮点

（1）通过暴力法以及分治法详细介绍“最近点对”问题的实现方法
（2）完成两种算法的图形界面可视化，使算法执行过程更清晰
（3）完成数据运行效率的对比
（4）自行绘制了算法示意图和算法流程图，实验展示更清晰
（5）完成了分治法在三维下的推广

二、实验内容与方法

1. 对于平面上给定的N个点，给出所有点对的最短距离，即，输入是平面上的N个点，输出是N点中具有最短距离的两点。
2. 要求随机生成N个点的平面坐标，应用蛮力法编程计算出所有点对的最短距离。
3. 要求随机生成N个点的平面坐标，应用分治法编程计算出所有点对的最短距离。
4. 分别对N=100,1000,10000,100000，统计算法运行时间，比较理论效率与实测效率的差异，同时对蛮力法和分治法的算法效率进行分析和比较。
5. 如果能将算法执行过程利用图形界面输出，可获加分。

三、实验步骤与过程

（一）一些准备工作

1、实验流程

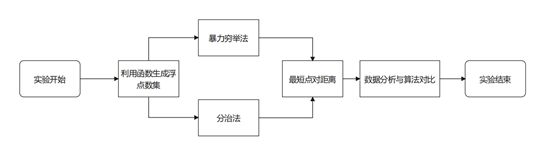
通过随机数生成器生成double型点集数据。然后对点对集合分别使用暴力穷举法与分治法进行运算，编程计算出所有点对的最短距离及运行时间，最后进行算法效率分析与对比得出实验结论。

2、数据生成与去除重复点

可以通过C++自带函数生成随机值。但随机值生成过程中有可能存在生成重复点的情况，因此需要对重复的点进行剔除。
在此我使用unordered_set结构并利用哈希完成对重复点的剔除。
①首先定义点结构体：

//定义点结构体  

struct Point {
     
    double x, y;
};

②重载比较函数与哈希函数

//重载比较函数
struct eqfunc {
     
    bool operator()(const Point &p1, const Point &p2) const {
     
        return ((p1.x == p2.x) && (p1.y == p2.y));
    }
};
	  
//重载哈希函数
struct hashfunc {
     
    size_t operator()(const Point &P) const {
     
        return size_t(P.x * 201928 + P.y);
    }
}; 

③使用函数生成数据并利用哈希对重复点进行剔除

//利用哈希函数进行去重
unordered_set<Point, hashfunc, eqfunc> hash;
//遍历赋值并哈希去重
for (int i = 0; i < length; i++) {
     
	point[i].x = dist(eng);
	point[i].y = dist(eng);
	if (hash.find(point[i]) == hash.end()) 	{
     
		hash.insert(point[i]);
		}else {
     
          i--;
        }
}

对于每个生成的随机数，分别赋值给横纵坐标，再利用哈希函数，如果在集合中找不到，则说明点未重复，则进行下一个点的生成。如果找到点，则将计数器自减1，并重新生成该点的横纵坐标值。

（二）暴力穷举法

1、算法描述

暴力穷举法即遍历求出每个点之间的距离，并选择距离最小的点进行输出。
具体流程图如下：

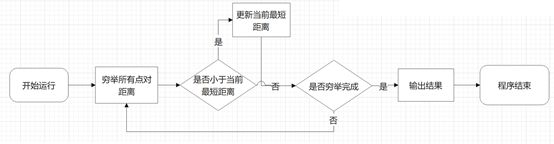
2、时间复杂度分析

不妨将问题看成一个求n边无向完全图的问题。则对于$n$个顶点有每个顶点存在连边$n-1$条，又因为是无向图，则共有连边$C=\frac{n\left(n-1\right)}{2}$。因此时间复杂度为$O\left(n^2\right)$

3、编程实现

double ans = INF; //设定初始结果为无穷大
for (int i = 0; i <= length - 1; i++)
{
     
    for (int j = i + 1; j <= length - 1; j++)
    {
     
        //遍历每一组可能，并选择最小值存入结果
        ans = min(ans, dis(point[i], point[j]));
    }
}

设置初始结果为INF。通过外层的循环遍历各点，再内层的循环遍历还未与当前点比较过的点，当发现存在两点间距离小于目前结果时，则更新结果值为更小的距离，依次循环穷举所有点对间距离。

（三）分治法

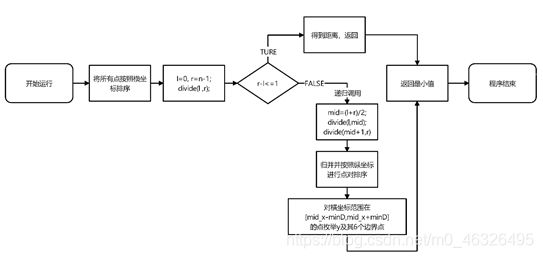
1、算法描述

基于暴力穷举法，我们在实际运算中不难发现，存在一些“显然距离很远”的点对，对这些点对的距离运算并进行比较常常是一种无用功，将造成时间空间的双重浪费。因此能否找到一种方法精简暴力穷举法，降低无用比较次数呢？
与排序算法类似，完成实验一后，不难发现：对于排序算法，快速排序与归并排序与其余三个排序算法比都是比较省时间的。这说明，将一个大整体分为几个小部分进行“分而治之”是解决类似问题的好方法。因此，相似地，我们可以使用分治法，利用“分而治之”的思想对问题实现简化。依据分治法，我们可以设计出如下算法：
①对所有点按照其横坐标进行排序；
②若$n=1$，返回无穷大；
$n=2$，计算距离并返回；
$n>2$，以该组数组下标中值分割，即mid=(l+r)/2,mid_x=point[mid].x，将规模为n的问题分解为两个规模为$\frac{n}{2}$的子问题并重复步骤②，直到得到两个子问题的解 mindis1,mindis2；
③合并子问题的点并将其按y坐标排序；
④设mindis为两个子问题解中的较小值，遍历当前规模下所有点，找出横坐标范围在[mid_x-mindis,mid_x+mindis]的所有点；
⑤将步骤④中的所有点与按y坐标排好序后的其后6个基准点（具体算法证明将在下面完成）进行比较，如果距离小于 mindis 则更新 mindis 的值。

具体流程图如下：

2、算法解释与正确性分析

（1）点集分块：
我们不妨将平面分为两个大致相等的点集再对问题进行考虑。

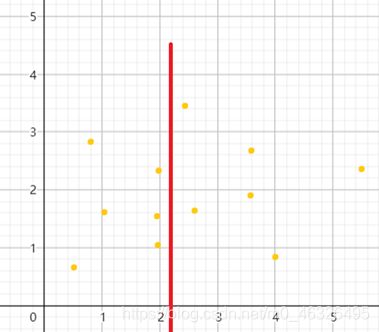
将平面的点分为两个点集，此时对于某点对中两个点p_1,p_2存在如下三种情况：
①$p_1,p_2$都位于左侧点集
②$p_1,p_2$都位于右侧点集
③$p_1,p_2$一个位于左侧点集，另一个位于右侧点集
对于情况①与②，可以通过递归进行解决，难点在于如何处理两个点不处于同一个点集的情况。

（2）鸽笼查找
不妨设左右两侧点集的最小距离为$d_l$,$d_r$。因此有如下结论：

左、右侧点集中每个点对间距离均分别大于等于$d_l$,$d_r$
因此，仅需对下图中蓝色方框内的异侧点对进行检测即可：

其中，$d=\min \left(d_l,d_r\right)$。
对于蓝色区域内的点，如果仍然采用暴力穷举法对每个点对进行检测，不能实质性降低时间复杂度以节省时间。因此，我们可以利用鸽笼原理，找到对应的基准点进行检测。
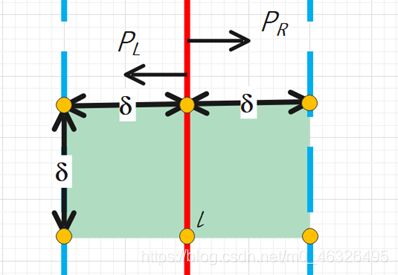
如下图，当对$\left[l-\delta ,l+\delta \right]$中的点进行归并后，这些点在数组中关于y坐标已经有序，不妨设最终情况为$p_L,p_R$两点分别位于点集$P_L,P_R$，且该点对间距离小于$\delta$，则$p_L,p_R$两点一定位于下图中$2\delta \times \delta$的浅绿色矩形内。这是因为根据分析，当且仅当点对位于该浅绿色区域内时，两点间纵坐标之差小于$\delta$，任何其他不在该范围内的点横坐标或纵坐标之差必定大于$\delta$，距离必定大于$\delta$，此时，该点对间距离一定不为最小，故无需进行比较。

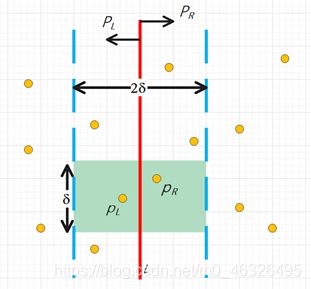
此时，对于下图中矩形左半边的$\delta \times \delta$正方形，因为$P_L$中所有点之间最小距离为$\delta$，依鸽笼原理，该正方形内最多有4个点（如下图）。类似地，$P_R$中也最多有4个点可以位于该$\delta \times \delta$正方形内。又因为两个正方形存在一条边完全重合，故有两个点为同一个点，因此在判断时只需判断每个点与其余6个基准点间距离关系即可。

（3）点集排序

对于算法中③合并子问题时，需要对点进行按照纵坐标的排序，此时不应直接在递归调用中使用排序算法进行排序。否则时间递归式将变为$$T\left(n\right)=2\times T\left(\frac{n}{2}\right)+O\left(n\log n\right)$$，最终时间复杂度将变为$$O\left(n{\log }^{2}n\right)$$。因此需要使用类似归并排序的思路，即将已经排序的数组$Y_l$和$Y_r$进行合并形成有序数组。

3、时间复杂度分析

①使用了归并方法后对纵坐标的排序在递归过程中的每一层都为线性效率，在具体算法实现中对每次递归中按照纵坐标的排序与归并排序中合并操作十分类似。即按照纵坐标将有序数组$Y_L,Y_R$进行合并从而形成有序数组Y。这是由于分治函数中当递归至仅有两个点时将直接合并并向上返回，因此，返回时待合并的两个数组$Y_L,Y_R$是有小规模合并而来，因此$Y_L,Y_R$一定是纵坐标有序的，继续合并后的数组也为纵坐标有序的数组，这样保证了每次操作一定范围内的点集时，点集内点都已经为纵坐标有序
通过分析算法，易得每次合并操作中比较的交换次数满足如下式子
$$\frac{1}{2}\left(right-left\right)\le n\le right-left$$
对于每次规模为$n=right-left$的合并操作，时间复杂度为线性的$O\left(n\right)$

②由①得，合并操作的时间复杂度为$O\left(n\right)$，对单个点的6个边界点的枚举操作时耗时为常数级，因此对单个点的枚举操作时间复杂度为$O\left(1\right)$。则对n个点的枚举总时间复杂度为$O\left(n\right)$

③不妨设程序消耗总时间为$T\left(n\right)$，每层递归时间消耗为$t\left(n\right)$。由于在程序刚开始执行时需要对所有点进行按照横坐标的排序，需要消耗时间为$O\left(n\log n\right)$，则有：
$$T\left(n\right)=t\left(n\right)+O(n\log n)$$
$$t(n)=\{\begin{array}{ll}2\times t\left(\frac{n}{2}\right)& \text{n>2}\\ O\left(1\right)& \text{n <=2}\end{array}$$

计算并化简得，$T\left(n\right)\propto n\log n$即该算法的时间复杂度为$O(n\log n)$

4、编程实现

（1）距离计算函数

//定义计算距离函数
double dis(Point p1, Point p2)
{
     
    return sqrt(pow((p1.x - p2.x), 2) + pow((p1.y - p2.y), 2));
}

（2）对点对进行以横坐标排序函数

bool cmpx(const Point &P1, const Point &P2)
{
     
    return P1.x < P2.x;
}

（3）分治核心函数部分：
①当仅有一个点时，直接返回无穷：

//如果只有一个点则返回无穷
if (left == right)
{
     
    return INF;
}

②当仅有两个点时，直接返回两点距离并对y进行排序

//如果有两个点则直接进行合并，并对y进行排序
if (left + 1 == right)
{
     
    close_p1 = point[left];
    close_p2 = point[right];
    point[left] = close_p1.y < close_p2.y ? close_p1 : close_p2;
    point[right] = close_p1.y > close_p2.y ? close_p1 : close_p2;
    return dis(point[left], point[right]);
}

③当点数大于二时，进行分治：
a.首先获得分治中点，并进行“分”的操作，并对点集进行以纵坐标的排序：

    //如果点数大于2
    int mid = (right + left) >> 1;                             //通过位操作快捷获得中点
    min_dist = min(Divide(left, mid), Divide(mid + 1, right)); //缩小问题规模实现“分而治之”
    Merge(left, mid, right);                                   //以y进行排序

b.记录跨中线且距离分治中点水平距离小于当前最小值的异侧点

// 使用temp数组记录跨线异侧点，并进行6个边界点的判断
Point *temp = new Point[right - left];
int i_size = 0;
for (int i = left; i < right; i++)
{
     
    //如果点在异侧且在最小距离内则记录入temp数组
    if (point[i].x > point[mid].x - min_dist && point[i].x < point[mid].x + min_dist)
        temp[i_size++] = point[i];
}

c.对每个在temp数组中的点进行6个检测点的判断

for (int i = 0; i < i_size; i++)
{
     
    for (int j = i + 1; j < i_size && j < i + 6; j++)
    {
     
        if ((temp[j].y - temp[i].y) > min_dist)
            //如果两个点的纵坐标之差大于当前最小值，则一定不符合条件，直接进行下一组判断即可
            break;
        if (dis(temp[i], temp[j]) <= min_dist)
        {
     
            //如果当前点距离小于等于当前最小值，则对最小距离进行更新
            min_dist = dis(temp[i], temp[j]);
            close_p1 = temp[i];
            close_p2 = temp[j];
        }
    }
}

d.所有运算完成后，返回当前分治的最小距离即可

return min_dist; 

（4）对点进行纵坐标排序：
首先完成对两侧点集的深复制，由于整个算法利用分治排序，可以借助分治排序的每次合并完成对点集的以纵坐标排序。由于排序前两侧点集已经有序，可以通过设置两侧点集的头指针对指针指向元素的值进行比较，并移动指针完成对所有点集的排序。当一侧点集排序完成后将另外一侧所有点直接顺序存入结果数组即可。

void Merge(int left, int mid, int right)
{
     
    //首先完成两侧点的深复制，
    int n1 = mid - left + 1; //左侧点集大小
    int n2 = right - mid;    //右侧点集大小
    Point *L = new Point[n1];
    Point *R = new Point[n2];
    //完成两侧点集的复制
    for (int i = 0; i < n1; i++)
        L[i] = point[left + i];
    for (int i = 0; i < n2; i++)
        R[i] = point[mid + 1 + i];
    //由于整个算法利用分治法，可以利用类似归并排序完成点对的纵坐标排序
    int i = 0, j = 0, k;
    for (k = left; i < n1 && j < n2; k++)
    {
     
        if (L[i].y < R[j].y)
            point[k] = L[i++];
        else
            point[k] = R[j++];
    }
    //如果归并时两侧数组存在剩余元素，则对剩余元素进行合并
    while (i < n1)
        point[k++] = L[i++];
    while (j < n2)
        point[k++] = R[j++];
}

（四）时间效率对比分析

正确性分析：
设计不同算法解决问题的基础是算法的正确性。通过随机数据生成了${10}^5$组大小为${10}^54的测试数据分别使用暴力穷举法和分治法进行求解最短距离并比较。均证明暴力穷举法和分治法可以得到相同的正确答案。因此证明了算法的正确性。

时间效率分析：
在本次实验中，我利用随机数生成器，随机生成了10组数据并取平均值作为某给定数量级下的运行时间，对${10}^1$~${10}^5$数量级下的每组相同数据分别进行了暴力穷举与分治法两种算法的运行时间测试。分别整理做表总结展示如下：
1、暴力穷举法

数量级	平均时间	平均时间对数	理论时间	理论时间对数
${10}^1$	0.00025	-3.60206	0.000278	-3.55542
${10}^2$	0.02805	-1.55207	0.027834	-1.55542
${10}^3$	2.79846	0.446919	2.7834	0.444576
${10}^4$	278.374	2.444629	278.374	2.444629
${10}^5$	28042	4.447809	27837.4	4.444629

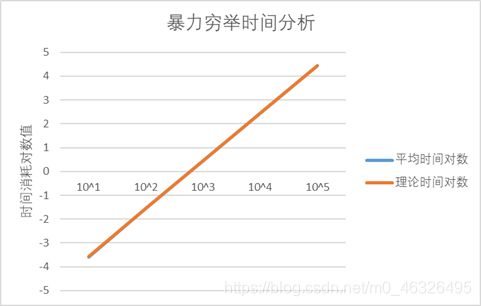
对于暴力穷举，由于算法未进行任何简化且算法执行次数与时间复杂度不随数据分布与数量级有任何变化，故整体拟合效果非常好，证明暴力法的时间复杂度为$O(n^2)$的结论正确。

2、分治法

数量级	平均时间	平均时间对数	理论时间	理论时间对数
${10}^1$	0.0043	-2.36653	0.001078	-2.967206
${10}^2$	0.03371	-1.47224	0.0215687	-1.666176
${10}^3$	0.38379	-0.41590	0.3235305	-0.490084
${10}^4$	4.31374	0.63485	4.31374	0.634853
${10}^5$	52.4283	1.71956	53.92175	1.731763

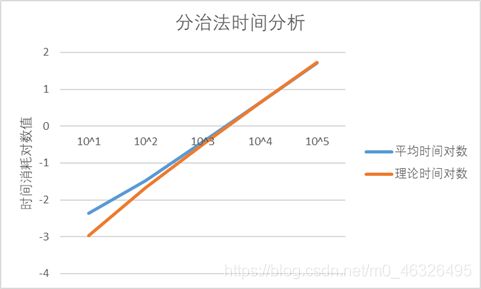
对于分治法，由于分治法需要开辟空间并实现递归操作，递归栈的迭代与开辟内存空间均需要消耗一部分时间。对于数量级较小的数据时，整个算法实际运行时间比较短，开辟内存空间与递归栈迭代消耗的时间的影响将被一定程度上放大。但当数量级较大时，这种影响被冲淡。因此会体现出当数量级较小时拟合效果较差，但当数量级较大时，拟合效果比较好。

3、两种算法分析对比

通过对算法时间的分析，可以看到，当对于小数量级的数据时（$10^2$以下），暴力穷举法要优于分治法，但当数量级较大时，分治法明显优于暴力穷举法。这是由于分治法需要开辟内存空间并通过递归栈实现递归。因此将消耗更多时间，并对小数量级下的最终时间消耗产生较大影响。
因此对于“最近点对”问题最明智的方法是当数量级小于${10}^2$时选择暴力穷举法进行运算，当数量级大于${10}^2$时选择分治法进行运算。

四、实验结论或体会

1、设计不同算法解决问题的基础是算法的正确性。在测试不同算法的时候，一定要保证不同算法的正确性。在本实验中，可以通过暴力穷举来验证分治法答案的正确性。
2、对于一些数学类问题，都可以通过数学分析并借助分治法进行求解，从而缩短程序的运行时间。例如：逆序对问题。
3、算法的时间复杂度一般由若干次常数级时间组成，因此减少算法运行时间时也应降低算法的常数级时间。例如本次实验中最后再计算平方根，中间比较过程可以比较距离的平方值。
4、图形界面可视化可以更清晰的展示算法的实现过程，有助于提升对算法的理解。例如本实验内，我使用Python完成了图形的可视化界面。
5、对实验结论进行合理推广并举一反三，由二维的最近点问题推广至三维的最近点问题，并进行了算法验证。

五、思考

在实验的过程中，我发现了一下问题，思考查阅资料后提出相关解决办法如下：
1、算法优化
每次比较都是通过比较距离进行的。而获得距离的操作可以分为做差、平方、求和再开方四个步骤。不妨省去开方，直接比较距离的平方值，最后再开方。从而一定程度上节省常数运算的时间。
以暴力穷举法为例，我利用随机数生成器，随机生成了10组数据并取平均值作为某给定数量级下的运行时间，对${10}^1$~${10}^5$数量级下的每组相同数据分别进行了优化前与优化后的运行时间测试，并做表如下：

数量级	优化前	优化后
${10}^1$	0.00025	0.00022
${10}^2$	0.02805	0.02496
${10}^3$	2.79846	2.49062
${10}^4$	278.374	247.752
${10}^5$	28042	24957.38

可以看出，大约节省了10%左右的时间。算法成功被优化了

2、点按照纵坐标排序问题
在算法实现过程中，需要在分治时实现对点按照纵坐标的排序。对于每层排序，若使用快速排序等排序方法将造成时间浪费。若直接调用排序算法，则有
$$T\left(n\right)=T\left(\frac{n}{2}\right)+O(n\log n)$$
最后解得$T\left(n\right)=O(n{\log }^{2}n)$，算法发生退化现象。不妨分析，在每层分治中，需要合并的两个子点集已经纵坐标有序，因此可以采用类似归并排序的方法实现每层排序。即设置两侧点集的头指针对指针指向元素的值进行比较，并移动指针完成对所有点集的排序。下移指针指向的元素较小的指针，直到遍历完整个点集。当一侧点集排序完成后将另外一侧所有点直接顺序存入结果数组即可。此时有
$$T\left(n\right)=T\left(\frac{n}{2}\right)+O(n)$$
解得最终时间复杂度为$O(n\log n)$节省了一定时间。

3、算法过程的可视化
为了对实验的点排序过程有更清晰深入的了解，我使用Python中的matplotlib函数库，实现了整个算法排序过程的可视化。清晰的展示了排序的具体过程。

4、分治法求最近点问题在三维下的推广
解决了分治法在二维下的最近点问题，尝试利用分治法解决三维下的最近点问题，发现有许多相似之处，进行编程实现并总结归纳。
（1）类比二维设计算法：
在解决三维的最近点问题时，不妨通过二维的最近点问题进行类比。

①使用分治法对空间进行划分：
类比二维的分治法，在三维坐标系V中，存在n个点依次记为$P_1,P_2,\dots ,P_n(n\ge 3)$。为了将这$n$个点尽可能均匀的划分到两个子空间$V_1{,V}_2$中，可以构造一个垂直于$x$轴的平面$x\left(P\right)=k$作为分割平面。其中$V_1=x\left(P\right)\le kx[P_1\in V,k\in N]和V_2=x\left(P\right)>kx[P_1\in V,k\in N]$。通过递归算法，可以计算出$V_1{,V}_2$中的最小点对距离$d_1{,d}_2$，令$d_m=\min (d_1{,d}_2)$

②分析跨界点：
第二步同样类比二维情况，求出$d_l=\min \left\{d_{ij}\left(P_i,P_j\right)|P_i\in V_1,P_j\in V_2\right\}$，即关于二分面的异侧点的最小距离。具体做法与二维分治类似：在第一次进行分割的原分割面$kx$的基础上做两个与之平行的切面$x_1=kx+d_m与x_2=kx-d_m\left(k\in N\right)$，将属于两切面之间的点按照z轴坐标进行排序。故属于$x_1\le x_i\le kx$范围内的点$P_i\left(x_i,y_i,z_i\right)$所能组成最短距离的另一个端点$P_j\left(x_j,y_j,z_j\right)$一定存在以下关系：$kx\le x_j\le x_2$，同时易知，与$P_j$组成最近点对的另一端点$P_i$，一定在以$P_i$为球心 ，以$d_m$为半径的半球面内，即有$$\left\{\sqrt{{\left(x_i-x_j\right)}^2+{\left(y_i-y_j\right)}^2+{\left(z_i-z_j\right)}^2}\le d_m|x_j>x_i\right\}$$。故只要找出上述两式的集合，即可得出需要进行判别的端点$P_j$所属的范围。与二维平面上相似，由于$P_i与P_j$中的点都具有稀疏性，因此，对于$P_i$中的任意一点，$P_j$中的点必定落在一个$d_m\ast \left(2d_m\right)\ast (2d_m)$的长方体中。即只需逐次比较$kx\le x_j\le x_2$空间与该外接长方体空间的交集空间内的所有点即可得到以$P_i,P_j$为端点的最短距离。

③鸽笼法确定临界点
由于鸽笼原理，依据$P_i$与$P_j$中的点都具有稀疏性，在$d_m\ast \left(2d_m\right)\ast (2d_m)$的长方体中至多存在24个满足条件的临界点。因此只需对这$24$个点进行距离检测即可，成功将每个点的距离比较时间复杂度从$O\left(n\right)$降至$O\left(1\right)$。

（2）算法设计
基于上面的分析，可以得到分治法求解三维最近点对问题的的伪代码如下：
设所有点的点集为$V$，分治函数名为Merge(Point* V)
①当仅有一个点时直接返回INF，当仅有两个点时直接返回两个点的距离并进行归并。
②当有三个及以上点时，对$V$中各点以$X$轴坐标进行快速排序，令$k$为$V$中排序后的中间分治点，使得
$$V_1=\left\{x\left(P_i\right)\le kx|P_i\in V,k\in N\right\},V_2=\left\{x\left(P_j\right)>kx|P_j\in V,k\in N\right\}$$
③令$d_1=Merge\left(V_1\right),d_2=Merge(V_2)$
④令$d_m=\min \left(d_1,d_2\right)$
⑤构造两个空间$W_1,W_2$，使得
$$W_1=kx-d_m\le x\left(P_i\right)\le kx|P_i\in V,k\in N$$
$$W_2=kx<x\left(P_j\right)\le kx+d_m|P_j\in V,k\in N$$
⑥对$W_1,W_2$空间中的点分别以y轴坐标进行排序，得到点集$W{Y}_1,W{Y}_2$，再分别以$z$轴坐标进行排序，得到点集$W{Z}_1,W{Z}_2$，此处需注意，仍然要采用类似归并排序的方法对点集进行排序，否则算法将退化
⑦对点集$W{Y}_1$的对应点集 $W{Y}_2$，从小到大对其判别空间中的$24$个临界点进行扫描，并返回最短距离$d_l$
⑧合并每层递归的结果，获得最终结果$d_{min}$

（3）时间复杂度分析：
通过与二维下的分治法进行对比可知，三维与二维的查差别仅在于对$y,z$都进行了排序，且由原来的$6$个临界点变成了$24$个临界点。故算法的时间复杂度仍然为$O(n\log n)$