双约束重力模型python实现,以物流需求预测为例
采用弹性系数发求得未来年份的物流生产量和吸引量,采用双约束重力模型对OD矩阵进行预测,阻抗函数采用的两两小区之间的距离,最后将预测结果矩阵写入excel。
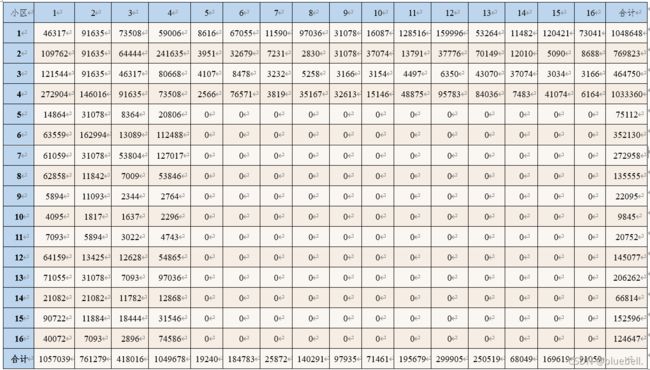
OD矩阵如图
程序如下:
import copy
import numpy as np
import pandas as pd
import openpyxl as op
"""
#################双约束重力模型########################
1.数据提取
2.物流生成预测
3.迭代求取ki,kj
4.物流分布预测
5.主函数
6.保存od_pre为预测od矩阵,保存od_draw_data为绘图数据
"""
# 弹性系数数据,求得物流增长率alpha
elastic_coefficient = [[0.12, 0.69], [0.1, 1], [0.08, 0.88]]
alpha = []
for each in elastic_coefficient:
alpha.append(each[0] * each[1])
# 提取od信息
od_data = pd.read_csv('L_OD_data.csv')
od_data = np.array(od_data)
od_data = od_data.tolist()
ai = od_data[-1] # 当前吸引量
pi = [] # 当前发生量
for i in od_data:
del i[0]
pi.append(i[-1])
del ai[-1]
del pi[-1]
area_number = len(od_data[0]) - 1 # 小区数
# 提取距离数据
f_ij = pd.read_csv('city_distance.csv', header=None)
f_ij = np.array(f_ij)
f_ij = f_ij.tolist()
# 物流生成预测的函数
def cal_ai_pi(alpha, year):
ai_pre = copy.deepcopy(ai)
pi_pre = copy.deepcopy(pi)
for i in alpha:
for index, data in enumerate(ai_pre):
ai_pre[index] = data * pow(1 + i, year)
for j in alpha:
for index, data in enumerate(pi_pre):
pi_pre[index] = data * pow(1 + j, year)
return ai_pre, pi_pre
# 迭代终止的判断函数
def judge(kj, kj_pre, ki, ki_pre):
for i, j, ii, jj in zip(kj, kj_pre, ki, ki_pre):
if i - j or ii - jj > 0.001:
break
return False
else:
return True
# 迭代ki,kj的函数
def cal_kij(ai, pi):
# 迭代
kj = [1 for i in range(area_number)] # 初始化kj
ki = [0 for i in range(area_number)] # 初始化ki,方便第一次比较
while True:
# 储存上一次的计算结果
kj_pre = kj
ki_pre = ki
# 迭代ki
ki = []
for i in range(area_number):
sum_row = 0
for j in range(area_number):
sum_row += kj[j] * ai[j] / f_ij[i][j]
ki.append(1 / sum_row)
# 迭代kj
kj = []
for ii in range(area_number):
sum_column = 0
for jj in range(area_number):
sum_column += ki[jj] * pi[jj] / f_ij[jj][ii]
kj.append(1 / sum_column)
# 终止条件的判断
if judge(kj, kj_pre, ki, ki_pre):
break
return kj, ki
# 通过od_data提取发生量和吸引量矩阵
l_od_temp = od_data[:-1]
l_od = []
for i in l_od_temp:
del i[0]
del i[-1]
l_od.append(i)
# print(l_od)
# 物流分布预测的函数
def cal_od_pre(kj, ki, ai, pi):
lod_pre = []
for i in range(area_number):
row = []
for j in range(area_number):
l_ij = ki[i] * kj[j] * pi[i] * ai[j] / f_ij[i][j]
row.append(l_ij)
lod_pre.append(row)
return lod_pre
def write_to_excel(fileName, lod, ai, pi):
#print(lod)
wb = op.Workbook() # 创建工作簿对象
ws = wb['Sheet'] # 创建子表
# 数据整理
titleString = [i + 1 for i in range(area_number)]
# 首行
titleString.insert(0, '小区'), titleString.append('实际求和值'), titleString.append('预测pi')
ws.append(titleString)
# 中间行,即od矩阵
for index, data in enumerate(lod):
#print(data)
data.insert(0, index + 1), data.append(sum(data)), data.append(pi[index])
ws.append(data)
# 倒数第二行
lost_row_2 = []
for column in range(area_number):
sum1 = 0
for row in lod:
sum1 += row[column + 1]
lost_row_2.append(sum1)
lost_row_2.insert(0, '实际求和值')
ws.append(lost_row_2)
# 最后一行
lost_row_1 = ai
lost_row_1.insert(0, '预测ai'),
ws.append(lost_row_1)
wb.save(fileName + '.xlsx')
def write_to_excel_to_draw(filName, lod):
# 将数据写入excel
wb = op.Workbook() # 创建工作簿对象
ws = wb['Sheet'] # 创建子表
for i in lod:
ws.append(i)
wb.save(filName + '.xlsx')
# 主函数,一个完整的预测步骤的函数
def main(stage):
# 物流生成预测
ai_pre, pi_pre = cal_ai_pi(alpha[0:stage + 1], 5)
# 计算kj,ki
kj, ki = cal_kij(ai_pre, pi_pre)
# 物流分布预测
lod_pre = cal_od_pre(kj, ki, ai_pre, pi_pre)
#print(lod_pre)
# 写入excel
fileName2 = 'od_draw_data' + str(stage + 1)
write_to_excel_to_draw(fileName2,lod_pre)
fileName1 = 'od_pre_' + str(stage + 1)
write_to_excel(fileName1, lod_pre, ai_pre, pi_pre)
# 计算第一个五年
main(0)
# 计算第二个五年
main(1)
# 计算第三个五年
main(2)
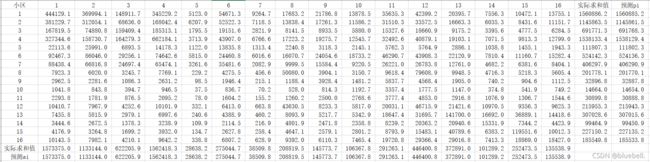
预测结果如下:
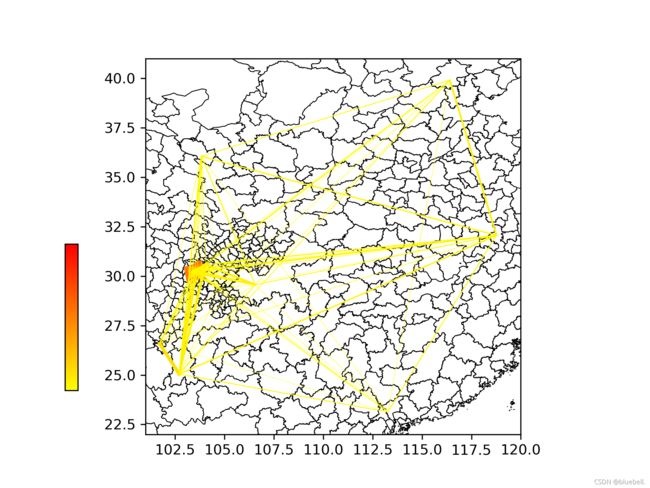
还可以通过matplotlib库和geopandas库绘制期望线图